对“鸡兔同笼”问题教学的认识和实践

■冯胜 邵承民

对“鸡兔同笼”问题教学的认识和实践

■冯胜 邵承民

如何准确理解和把握课改新增加内容，从而进行有效的教学，让学生在学习的过程中更好的理解数学本质，建立数学模型，感悟数学文化，已成为小学数学教学研究的课题。“鸡兔同笼”问题就是伴随着数学课程改革出现在小学数学教科书中“数学广角”学习板块的“新”内容。其实，“鸡兔同笼”问题是我国民间流传下来的一类数学妙题，是前人探究出来的知识成果，它集题型的趣味性、解法的多样性、应用的广泛性于一体，堪称历史经典，以往仅出现在“奥数”作为对学生进行思维训练的素材。作为小学数学教材中的这一新增内容，其教育功能与价值并不完全是要求学生解决“鸡兔同笼”这个数学问题，更重要的是让学生在解决问题的过程中建立解决这类数学问题的数学模型，在数学思考中逐步感悟数学思想。笔者曾参与“鸡兔同笼”一课的教学研究，在此与大家分享对这节课的教学认识和实践。

1.充分尊重学生的已有知识经验，在自主探讨中，体验数学乐趣

建构主义教学论认为：知识是不能被传递的，而是基于主体经验的主动建构，应针对学习者已有的经验和兴趣，发挥学习者的主动作用。因此，在教学中必须充分尊重学生的已有基础，发挥他们的主动性，赋予他们有话说、有事做的权力，参与数学教学活动。

鸡兔同笼这一数学问题对于学生来说并不陌生，有的学生在数学读物上看过，有的学生在数学兴趣小组中学习过，甚至有的学生能还能运用多种方法解答。但是，还有许多学生不会解决或会解决却不知其所以然。所以，在教学中既要让学生运用各种途径大胆地尝试解决，体验在解决问题中带来的成功与乐趣，又要让学生明确本节课的目的。为此，我们进行了如下设计：

播放关于古代数学专著《九章算术》和《孙子算经》的短片，引出鸡兔同笼问题。让学生对问题解释后，将问题“笼子里有若干只鸡和兔。从上面数，有35个头，从下面数，有94只脚。鸡和兔各有几只？”简化成例1：“笼子里有若干只鸡和兔。从上面数，有8个头，从下面数，有26只脚。鸡和兔各有几只？”。在学生理解题目的基础上，运用自己的方法尝试解决。

在这个教学过程中，学生在观看短片的过程中感受到我国古代数学文化的博大精深，同时也在将原问题简化成例1的过程中，体会到“化繁为简”这一重要的数学思想方法。对于例1来说，学生现阶段的知识水平，是完全有能力解决的。

【课堂再现】

生1：我是先猜鸡有4只，兔也有4只，但是4×4＋4×2=24只脚，不满足条件，我接着猜鸡有3只，兔有5只，3×2＋5×4刚好等于26只脚，说明我猜的是正确的。

生2：我是把鸡和兔只数的每种情况列举出来，就找到满足条件的情况。

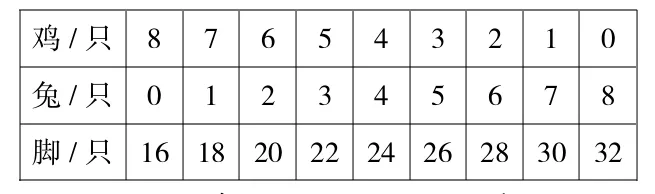
鸡/只8 7 6 5 4 3 2 1 0兔/只0 1 2 3 4 5 6 7 8脚/只16 18 20 22 24 26 28 30 32

生3：我是运用假设法解决的。……

可以看出，学生对问题的解决方法是多样的，思维水平也是不同层次的，学生1的方法是运用假设检验法，学生2的方法是列举法，学生3的方法是假设法。

2.有效把握课堂合理的生成资源，在启发引导下，建立数学模型

虽然“假设检验法”和“列表法”非常直观、易懂，学生容易接受，但是两种方法的缺点也很明显，如果题目的数据较大，则不宜采用。因此，我们将这节课的教学重点确定为理解“假设法”这一数学思想方法。如何利用现有的课堂生成资源，帮助学生建立“假设法”解决这类问题的数学模型，并让学生在解决问题的过程中，获得数学思维的提升呢？

首先，我们利用学生呈现的运用列表法解决例1的表格，请学生思考：观察表格，从中你能发现什么规律吗？学生观察交流后，帮助学生归纳出：在鸡与兔总只数不变的情况下，鸡每减少一只，兔就增加一只，总脚数增加两只，反之，鸡每增加一只，兔就减少一只，总脚数减少两只。

还要让学生自己发现假设检验法和列表法的局限性，通过让学生思考后明白，采用这种假设检验的方法或者列举的方法是可以找到答案的。然后，教师再提问：你能用这两种方法解决前面的“鸡兔同笼”问题吗？显然，学生在比较中对几种解答方法进行了适当的评价。

要通过教师的有效教学帮助学生理解假设法并能正确运用，就必须回答假设法是什么。我们认为是运用极端假设进行的消元。正因为两个事物能够转化成一个，所以才“全假设成鸡”或“全假设成兔”。我们进一步思考：如果不“全假设成鸡”或“全假设成兔”，而是“任意假设鸡兔”，可以吗？答案也是肯定的。

比如例1中，我么们假设有4只鸡，4只兔，此时脚数为4×2＋4×4=24（只），比实际26只脚多了26-24=2（只），说明兔假设少了，而鸡假设多了。兔少了多少呢？（26-24）÷（4-2）=1（只），所以，鸡有4-1=3（只），而兔有4＋1=5（只）。

我们不是让学生直接的从我们这里获得假设法解题的模式和步骤，而是让学生经历假设法的产生过程，只有这样学生才不拘泥于“模型”，为学生的思维发展留下足够的空间。

【课堂再现】

师：我们来大胆猜测一下这道题的结果吧。谁愿意来猜一猜？

（相机板书，如：鸡16只，兔19只；鸡30只，兔5只）

师：第一个同学猜对了吗？怎样来验证？（列式：16×2＋19×4=108）算出来是108只脚，脚多了说明了什么？

如果要你们在这个基础上接着猜，你们会怎样猜呢？（指2～3名学生回答）为什么你们都减少兔增加鸡呢？

学生回答后，教师小结：因为一只兔比一只鸡多两只脚，所以脚多了的时候应该减少兔增加鸡。教师引导学生朝着这个方向再猜，（如：鸡20只，兔15只。列式：20×2＋15×4=100）脚还是多了，还要减少兔增加鸡。

师：看来，只要找对了方向，像这样继续猜下去，我们也可以找到答案。接下来请大家像刚才这样验证第二组猜测，如果不对，请试着进行调整并找到答案，数一数，你做了几次调整。

（学生活动，教师巡视，参与讨论并及时给予辅导。指名学生展示自己的猜测过程，教师引导其他学生及时作出评议）

师：刚才老师发现有的同学调整了5次找到了答案，有的同学只调整了2次就找出答案了。想一想，能一次就调整出答案吗？

（学生回答，教师引导学生进一步明确增加a只兔，就减少a只鸡，相应的就增加2a只脚；反之，增加a只鸡，就减少a只兔，相应的就减少2a只脚）

师：多么有智慧的调整啊！这个调整的过程怎样用算式表示呢？

学生思考后，指名板演：

鸡30只，兔5只

30×2＋5×4=80（只）

94-80=14（只）

14÷（4-2）=7（只）

30-7=23（只）……鸡

5＋7=12（只）……兔

学生列式后，引导其他学生评议并提出问题，明确“4-2”表示什么，求出的“7”又表示什么？教师再将前面的“鸡30只，兔5只”改为“假设鸡有30只，兔有5只”。

师：其实，我们也可以首先假设鸡是0只，兔是35只，也就是假设笼子里全是兔；或者首先假设鸡35只，兔是0只，也就是假设笼子里全是鸡。请你选择一种，列出算式，解决问题。

指名板书计算过程：假设笼子里全是鸡。

35×2＋0×4=70（只）

94-70=24（只）

24÷（4-2）=12（只）

0＋12=12（只）……鸡

35-12=23（只）……兔

师：像这样首先假设一种情况，再根据题目中的条件进行分析调整，直到找出答案的方法就是假设法。比较这两种假设方法，你认为哪种更简便？（学生自由评议）所以在解答类似的问题时，我们一般都采用后面的这种假设情况。

赠人以金，何如授人点金之术？授人以渔，可以渔尽天下之鱼！

3.及时丰富多样的教学素材，在应用拓展中，感悟数学魅力

由于“鸡兔同笼”问题解题方法的特殊性（假设法），许多应用问题都可以化为“鸡兔同笼”问题。因此，我们以问题解决和生活应用强化、拓展新知，把“假设法”运用到具体的生活问题中，将学生的思维向纵深发展，感悟数学魅力。

于是在学生学习假设法之后，呈现了下面的两个问题：

（1）有龟和鹤共40只，龟的腿和鹤的腿共有112条。龟和鹤各有几只？

（2）全班一共有58人，共租了12条船。每条大船坐6人，每条小船坐4人，恰好全都坐满。大小船各租了几条？

让学生思考，这两个问题与“鸡兔同笼”问题有联系吗？有怎样的联系？让学生思考后发现：“鸡兔同笼”问题不仅仅是单纯是指鸡和兔的问题，还有许多数学问题可以化归成这类问题，运用假设法去解答。最后，让学生独立地解答这两个问题。

由此可见，掌握“鸡兔同笼”问题的基本解法，经过适当的转化和迁移，可以解决更加广泛的数学问题。与此同时，通过日本民间流传的“龟鹤算”与身边的现实问题，使学生领悟数学建模。这样一个首尾呼应的课堂结构，使学生更深刻地感受数学课堂的完整性，同时又让学生浸染在古今中外数学文化交融的氛围中，使数学课堂也沐浴着深厚的人文气息。

（作者单位：冯胜华中科技大学附属小学邵承民武汉市硚口区武药小学）

责任编辑 廖林