例谈在变化中寻找临界条件
2010-03-20朱连生
朱连生
(德兴一中 江西德兴 334200)
临界现象是物理中常见的现象,也是高考热点之一.很多同学对此问题无从下手,或者知道找临界条件,但只是静态地停留在一个状态(点)去研究临界问题,而不是认真细致地研究变化的过程、以及各物理量发生变化的规律,很难发现事物发展的本来面目.
现以一道试题为例.
【试题】一弹簧一端固定在倾角为37°光滑斜面的底端,另一端拴住一质量m1=4 kg的物块P.Q为一重物,已知Q的质量m2=8 kg.弹簧的质量不计,劲度系数k=600N/m.系统处于静止,如图1所示.现给Q施加一个方向沿斜面向上的力F,使它从静止开始沿斜面向上做匀加速直线运动.已知在前0.2 s时间内,F为变力;0.2 s以后,F为恒力.求力F的最大值与最小值.(g=10m/s2)
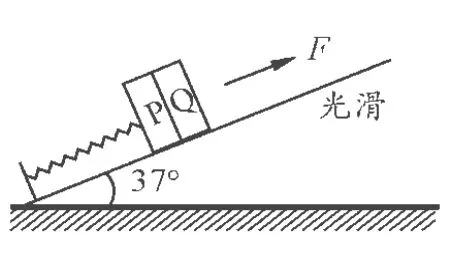
图1
本题得分率相当低,全部做对的同学即使在重点班也是凤毛麟角.归纳起来,主要有以下两种错解方式.
错解一:以PQ整体为研究对象,由系统原先静止时受力分析,有
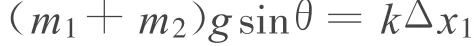
当PQ一起沿斜面匀加速上滑至二者恰好脱离时,弹簧为原长,则一起上滑的位移
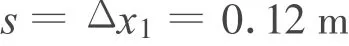
解得
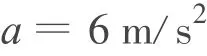
PQ刚从斜面上一起向上匀加速运动时
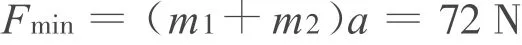
P
Q刚分离时
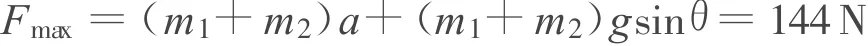
错解二:以PQ整体为研究对象,当系统原先静止时受力分析,有
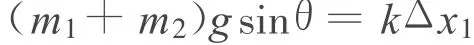
当PQ一起沿斜面匀加速上滑至恰好脱离时,PQ之间的压力为零,P受力平衡,有
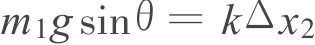
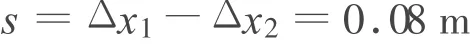
PQ刚从斜面上一起向上匀加速运动时
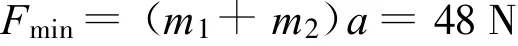
PQ刚分离时
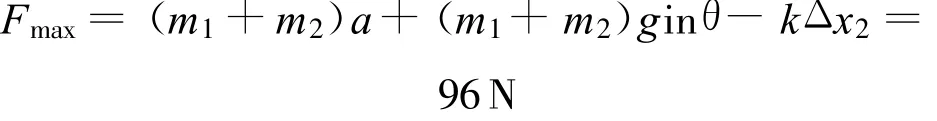
究其错误原因,都在于不善于找出PQ恰好脱离这一临界状态下所满足的条件.解法一太武断,想当然地认为PQ刚脱离时弹簧为原长;解法二停留在一个状态(点)去研究临界问题,对各物理量的变化缺乏细致地分析,认为PQ刚脱离时受力平衡,即a=0,以致于难以找到解决问题的有效方法.
临界现象在物理中常见.当物体由一种物理状态变为另一种物理状态,存在一个过渡的转折点,这时所处的状态通常称为临界状态,与之相关的物理条件则称之为临界条件.题干中常用“恰好”“最大”“至少”“不相撞”“不脱离”等词语对临界状态给出了明确的暗示.审题时,一定要抓住这些特定的词语,发掘其内在规律,找出临界条件.然而,临界条件通常具有一定的隐蔽性,灵活性较大.那么如何求解临界问题呢?反思之余,下面结合笔者在教学工作中的一点心得体会与大家共同交流、探讨.
解决临界问题,最重要的是要抓住临界问题的临界条件,必须细致分析各物理量的变化情况,在变化中去研究,即不能停留在一个状态(点)去研究临界问题,而是要研究变化的过程、变化的各物理量,寻找临界条件,具体基本思路如下.
1 认真审题,联想物理情境,弄清问题中物理过程变化的细节
审题时,应力图还原该题的物理情境,弄清物理过程的细节,分析整个过程中有几个阶段,在一些变化的过程中,物理量之间的对应关系如何发生变化.比如,物体所处的平衡状态的破坏,物体运动方向的改变,绳子的断裂,某物体跟另一物体相脱离或相对滑动,圆周运动物体通过最高点,带电粒子通过电场或磁场的边界,光线从光密介质射入光疏介质时折射角等于90°等,往往会出现临界状态,这就要求我们作认真细致地分析.
【例1】如图2所示,在匀速转动的水平圆盘上,沿半径方向放置两个用细线相连的质量均为m的小物体A、B,它们到转轴的距离分别为rA=20 cm,rB=30 cm.A、B与盘面间最大静摩擦力均为重力的0.4.试求:
(1)当细线上开始出现张力时,圆盘的角速度ω0.
(2)当A开始滑动时,圆盘的角速度ω.
(3)当A即将滑动时,烧断细线,A、B运动状态如何?(g取10m/s2)
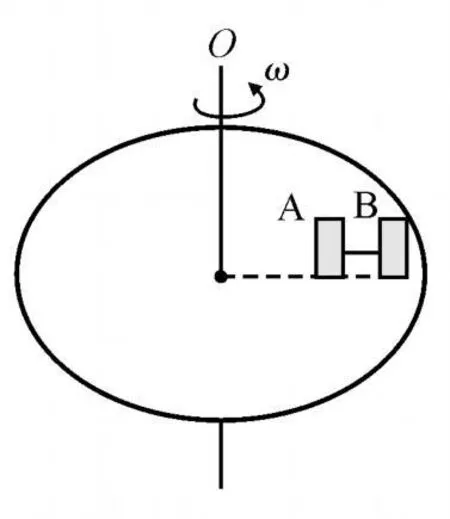
图2
分析:很多同学对于本题束手无策.然而通过研究各物理量的动态变化过程,不难发现,最初圆盘转动角速度较小,A、B随着圆盘做圆周运动所需的向心力较小,可由A、B与盘面间静摩擦力提供.由于rB>rA,由公式F=mω2r可知,B所需向心力较大;当B与盘面间静摩擦力达到最大值时(此时A与盘面间静摩擦力还没有达到最大),若继续增大转速,则B将做离心运动,从而拉紧细线,使细线上出现张力,转速越大,细线上张力越大,使得A与盘面间静摩擦力增大.当A与盘面间静摩擦力也达到最大时,A将开始滑动.概括地讲,本题中A、B间若没有细绳连接,则当转速增大到B可开始滑动时,A并不滑动,这时A、B间距离增大;若A、B间有绳连接,当B即将滑动(Ff达到Ffm)时绳才有张力,且之后直到A即将滑动前,B所受的摩擦力都为最大静摩擦力.
解:
(1)对B

代入数据得
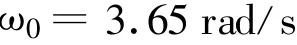
(2)分析A开始滑动时,A、B受力情况如图3所示,根据牛顿第二定律
对A
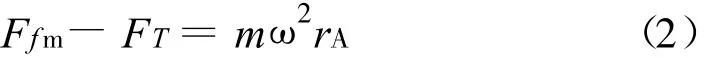
对B
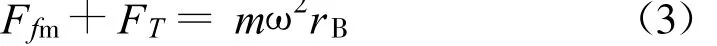
其中

联立式(2)、(3)(4)解得
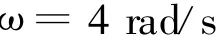

图3
(3)烧断细线,FT消失,A与盘面间静摩擦力足以提供向心力使A继续随圆盘做圆周运动,而B由于Ffm不足以提供向心力而做离心运动.
2 寻找过程中变化的物理量,探求各物理量的变化规律
某一过程中,涉及的物理量主要是力、加速度、速度、位移等.在分析此类问题的时候,主要抓住力的变化,因为力是决定物体运动的主要因素.要着重分析力的大小变化规律、方向变化规律、受力数目的变化、力的性质的变化(如静摩擦力转化为滑动摩擦力)等;同时还要兼顾加速度、速度、位移等的变化情况.这些变化往往蕴含着临界状态的出现,此时有利于我们找到临界条件.
【例2】一块木板静止在光滑水平面上,木板质量M=4 kg,小滑块m=1 kg,小滑块在木板的右端,它与木板的动摩擦因数μ=0.4,g=10m/s2,如果用一个水平向右的力作用在木板M上,则
(1)滑块与木板发生相对运动的力F至少要多大?
(2)如果F=5N时,滑块的加速度是由4N的摩擦力提供,而木板的加速度是F-f=1N的合力来提供,这样不是滑块的加速度大于木板的加速度吗?这样不是会使滑块在右端滑落吗?可事实上这是不可能的,为什么?
解析:随着作用在木板的水平外力的增大,系统的加速度增大,滑块仅依靠静摩擦力产生加速度,直到静摩擦力达到最大静摩擦力,此时能产生的最大加速度是多大,这个加速度就是相对滑动的临界加速度.本例中,力F作用在木板上,则小滑块仅受静摩擦力能产生的最大加速度是μg=4m/s2.因此使小滑块相对木板滑动的最小拉力 μg(m+M)=20 N.若拉力F<20N,则小滑块相对木板静止,仅依靠静摩擦力产生加速度;若F>20N,则小滑块相对木板滑动.
3 确定临界状态,分析临界条件
显然,分析变化过程,确定物理量变化的规律,是解决问题的关键,从而确定临界状态,挖掘隐含的临界条件,利用已学的物理规律表达各物理量之间的关系.当然要求解临界问题,还经常涉及到一些极值问题,往往伴随不等式的应用,自然而然也就会牵涉到一些与之相关的数学知识:三角函数、定积求和、定和求积、二次方程判别式等.
由此,对文章伊始提出的考试题,若在变化的过程中,分析临界条件,可知PQ刚要脱离时PQ之间的压力为零,但a不为零,因为此前一直沿斜面匀加速运动.不难得到正确解答.
正确解法:以PQ整体为研究对象,对系统原先静止时受力分析,有
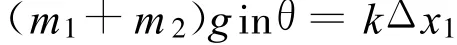
当PQ一起沿斜面匀加速上滑至恰好脱离时,PQ之间的压力为零,以P为研究对象,进行受力分析 ,可得
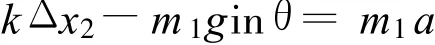
PQ刚从斜面上一起向上匀加速运动时
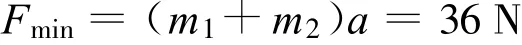
PQ刚分离时
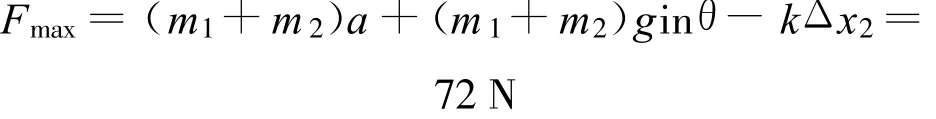
1 张传霞.创新设计高考总复习.西安:陕西人民出版社,2007.57
2 王朝银.步步高高考总复习.哈尔滨:黑龙江教育出版社,2009.60,77
