浅谈分类思想在中学物理解题中的应用
2010-03-20辉志文
辉志文
(凤庆二中 云南凤庆 675900)
分类思想在解析综合性问题尤其是学科内综合问题时常常用到,是考查学生综合分析能力、逻辑推理能力、探索能力和严谨的程序思考能力的一种思想方法.
下面是分类思想在物理解题中运用的几个入门示例.
1 某一物理量取值不同,分类讨论该物理量
由某一物理量的取值不同,使得物理过程不同,需要采用不同的物理规律,导致待求物理量表达式表示不同的物理意义,需要分类讨论.
【例1】如图1所示,金属棒a在高h处从静止释放,沿粗糙的弧形导轨滑到底部进入光滑水平导轨.水平导轨处于竖直向下的匀强磁场中其右侧静止放置另一导体棒b,a、b的质量均为m.已知两导体棒始终未相碰,且达到稳定后,b棒以v匀速向右运动.试求:
(1)棒a在弧形导轨上克服摩擦力做的功;
(2)若在原水平导轨右侧接宽度减半的光滑平行导轨,且棒b进入窄轨道后经过时间t达到稳定状态,则此过程中产生的电能是多少[1]?
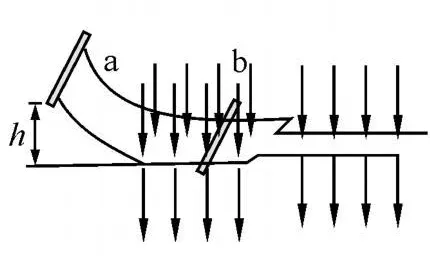
图1
分析:在光滑水平导轨上,b最终以v匀速向右运动,且达到稳定状态.所以无论b还是a都应该处于平衡状态,故a最终也以v匀速向右运动,此时a、b所受的安培力大小相等,方向相反,系统动量守恒,有
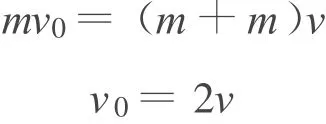
结合动量守恒及动能定理解得棒a在弧形导轨上克服摩擦力做功W摩为
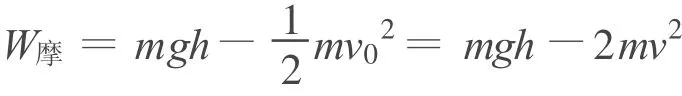
由于窄轨道接在弧形轨道右侧,a、b都在弧形轨道上达到第一次稳定速度,即速度都为v.当b进入窄轨道后,直到a也即将进入窄轨道前,a受到的安培力为b的2倍.若经过t后a还在原轨道,动量不守恒,但磁通量 Υ不变,且整个过程中通过两棒的电荷量q相同.对a,当 Δt※0时,由动量定理得
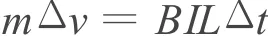
求和得

同理,对b得
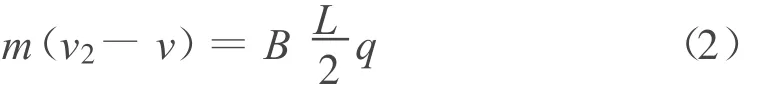
可解得
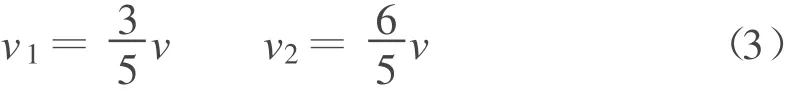
由于b从静止开始,且a、b之间的能量靠安培力传递,故b获得的能量是安培力做功的结果,属于回路中产生的电能,则
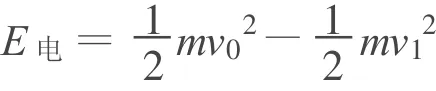
当a在原轨道运动的时间t1 小结:E电大于初动能是因为所求的是整个回路产生的电能,它包括回路消耗的电能、转化中先转化为电能、再转化为动能的部分,故出现电能大于初动能,不是创造了能量,能量是守恒的.这是发电机、电动机结合的模型. 对比较复杂的非数值问题,采用数学规律分析时,需要讨论数学方程的解是否与物理事实一致. 【例2】长为L,质量为M的圆柱形木棒竖直放置,在其顶部套有质量为m的铁环,当棒与环相对滑动时环与棒间有大小恒为kmg(k>1)的摩擦力.现突然在棒的下端给棒一个很大的冲击力,使棒在瞬间具有竖直向上的速度 v0.求棒上升的最大高度[2]. 分析:以地球为参照物,取向上为正方向,对环和棒受力分析,并运用牛顿运动定律结和运动学公式且假设环与棒在时间 t内的相对位移恰等于棒长,得 解得 其中 若(1)式t存在两个相等的实数根,即 时,环与棒恰不分离,解得 此时(1)式的解为 棒与环相对运动的末速度就是棒做竖直上抛运动的初速度,棒能上升的最大高度为 其中 若(1)式无实根,即 若(1)式存在两个不相等的实数根,即 时,说明环与棒在还没获得相同速度时就已经分离,此时环与棒的加速度都发生突变,变为-g,且此后恒为-g,即环与棒分别做竖直上抛运动.所以(1)式两根中,较大的根与物理事实不符,应舍去. 此时 【例3】光滑水平面上有大小相同的A、B两球,质量分别为m1、m2.开始时B球静止,A球沿两球连心线方向以速度v0向B球运动并发生碰撞.已知两球在形变恢复阶段的相互作用冲量是形变压缩阶段相互作用冲量的K倍,试求: (1)两球形变最大时各球的速度v1、v2; (2)碰后各球的速度[3]v1′、v2′. 分析:此题涉及到恢复系数问题,由于恢复系数取值不同导致碰撞类型和碰后两物体运动情况不同,需要分类讨论. 例如对万有引力定律及库仑定律教学就需要分类讨论.第一,两个定律虽然形式相同,但使用范围不同,有质量的物体间都存在万有引力;库仑定律只适用于点电荷间的相互作用.第二,场源不同,万有引力相互作用较弱;电场相互作用相对较强. 总之,分类讨论思想是研究和解决物理问题的重要思想方法之一,是一种逻辑推理方法之一,也是科学研究中最常用最基本的方法之一.我们常以“物以类聚”来认识自然界中成千上万的事物,又以“分门别类”来研究纷繁复杂的事物对象,这其实就是分类讨论思想方法在认识事物时的具体运用.所以今天我们学习分类讨论思想,不仅仅为了解决物理问题,而是在学习一种进行科学研究的本领及方法论. 1 王良调,等.联想解题.长春:吉林人民出版社,2000:750~752 2 胡开文,等.北大考典(物理).北京:北京大学出版社,2005:71~72 3 陈一生.大学物理(上册).天津:天津大学出版社 :61~ 63
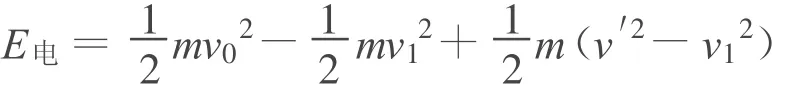
2 分类讨论比较复杂的非数值问题
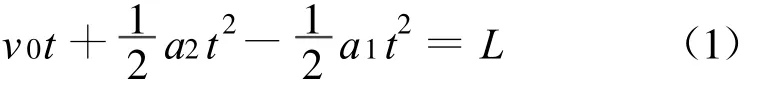
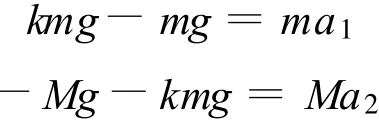

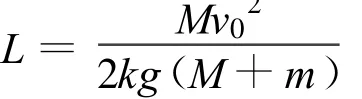



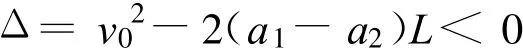
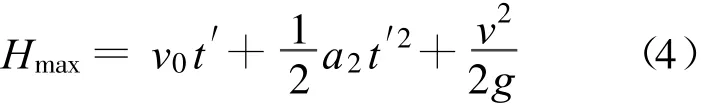
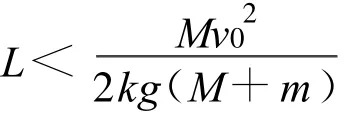


3 分类讨论涉及恢复系数的碰撞问题
4 分类讨论涉及形式相同的定理公式
