天体距离是如何测定的
2010-03-19西南大学地理科学学院400715邵发仙
西南大学地理科学学院(400715) 邵发仙
天体距离是如何测定的
西南大学地理科学学院(400715) 邵发仙
在高中地理教材必修一“宇宙中的地球”部分教学过程中,我们经常会遇到“光年障碍”。在描述星系、天体到地球的距离为××光年时,教师总会提醒学生光年是距离单位而不是时间单位,1光年是指光在一年中传播的距离(1光年=308568千米)。例如:太阳到银河系中心的距离为2.6万光年,最近河外星系的距离约16万光年,可观测的宇宙范围约150亿光年。学生可能会追问,几十万光年岂不是光从地球到该天体要走几十万年,谁能活得足够久等到光返回啊?那么天体距离是如何进行测量的呢?
由于各种天体距离尺度不一,我们所选择的测量方法也不尽相同。
一、月球与地球的距离
18世纪以来,人们传统上用三角视差法测定月球到地球的距离;近年来随着科学技术的进步,人们逐渐用雷达和激光测量月地距离。
1. 三角视差法

图1
几何学中有“角边角定理”,即已知三角形两角及其所夹之一边即可求解该三角形。三角视差法就是基于这一原理。视差是观测者在两个不同的位置看同一个天体的方向之差。
图1中M为月球,角P叫做地平视差,根据三角函数可得公式:(R为地球半径,L为月球到地球的距离),则月地距离:
由于地心不能到达,实际测量时是通过地面上处于同一子午线的两地来达到目的。世界上第一次测定地月距离,是1715年至1753年,法国天文学家拉卡伊和他的学生拉朗德,在基本上位于同一子午线的柏林和好望角测得。
2. 雷达法
无论可见光还是无线电波,本质上都是电磁波,传播的速度都是光速,差别在于频率和波长不同。雷达的信息载体是无线电波,雷达设备的发射机把电磁波能量射向空间某一方向,处在此方向上的物体反射其碰到的电磁波,雷达接收此反射波,送至接收设备进行处理,提取有关该物体的某些信息,如距离、方位、高度等。测量距离实际是测量发射脉冲与回波脉冲之间的时间差,因电磁波以光速传播,据此就能换算成目标的精确距离。
如:根据从地球发往月球脉冲信号的时刻和返回时刻,得到信号往返所用的时间t,求出月地距离:
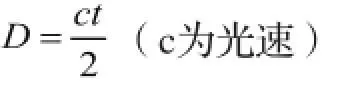
激光技术问世后,人们用激光雷达代替无线电雷达,由于激光的方向性好,光束集中,单色性强,故观测精度比无线电雷达高。但无论是无线电雷达还是激光雷达都存在一个硬伤,那就是在人的生命周期中,难以克服远距离观测时需要的时间。
二、太阳与地球的距离
由于太阳表面无固定标志,没有可供参考的准确目标,加上太阳距离地球比月球远得多,地平视差很小,难以准确测量,太阳辐射强烈等原因,所以三角视差法不适用于测量太阳与地球的距离。又因为太阳是炽热的气体球,不可能反射雷达波和激光波,所以也不能用雷达测距法测量日地距离。
早期测定太阳的距离需要借助离地球较近的火星或小行星。先用三角视差法测定火星或小行星的距离,再根据开普勒第三定律求日地距离。
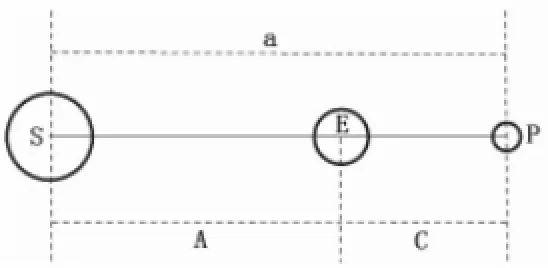
图2
图2中,S代表太阳,E代表地球,P代表火星。当火星大冲时,火星距地球最近,设此时日地距离为A,太阳与火星的距离为a,火星与地球的距离C=a-A(C值已由三角视差法测知)。因此只需知道太阳与火星的距离a,就能计算出日地距离。
根据开普勒第三定律:行星到太阳距离(a)的立方比,等于它们公转周期(T)的平方比T2=a3———就能计算行星到太阳的距离则日地距离可得:A=a-C。
三、恒星与地球的距离
恒星距离我们非常遥远,测定其与地球的距离非常困难。目前已有多种测定恒星距离的方法,下面介绍几种:
1. 三角视差法
三角视差法测定恒星距离时所采用的基线不再是地球半径,而是地球公转轨道半径。早在哥白尼的时代,人们就想到地球公转过程中观看较近的恒星时,该恒星会在遥远的天球背景上不断改变位置,地球绕日公转一周,该恒星就应在天球上画一个小椭圆,这叫恒星周年视差位移。
如图3所示,我们把地球公转轨道看作近圆形,取恒星和地球之间的连线,恰好与地球公转轨道半径相垂直,此时地球公转轨道半径对恒星的张角达到最大值, 此角就叫做恒星周年视差,即恒星、地球和太阳构成的直角三角形的最小角。地球位于公转轨道的A时,地球上的观测者看到恒星位于天球的A'点,半年后当地球位于公转轨道的B时,观测到恒星位于天球的B'点。这两点之间的角距离的一半,就是恒星的周年视差。由此可见,恒星的周年视差可由相隔半年的2次恒星位置的测定计算出来:
恒星周年视差以地球轨道半径为基线,观测者必须要等到半年之后才能再次测定它的位移。此方法对300光年远的恒星,观测误差已达到视差自身的量级,所以这种方法目前还仅适用于测定距离为300光年范围内的恒星。
2. 分光视差法
更遥远的恒星,由于周年视差非常小,三角视差法就鞭长莫及了。所以20世纪以后又有了分光视差法,通过对恒星光谱分析测定其距离。

图3
观测到的恒星的明暗程度称为亮度,天文学上用视星等表示。视星等与其距离的平方成反比。所以,天体的亮度并不能表示其发光本领。为了比较不同恒星的真实发光能力,必须假想将他们移到相同的距离上。天文学上把这个距离定为10秒差距(pc),天文距离单位通常有天文单位(AU)、光年(ly)和秒差距(pc)三种。太阳与地球间的平均距离叫做1天文单位,光在一年内所通过的距离叫1光年,秒差距是一个天文单位所张的角度为一角秒所对应的距离。1秒差距=3.2616光年=206265天文单位=308568亿千米,在标准距离处的恒星的亮度为绝对亮度,其星等称为绝对星等。恒星的绝对星等能够由恒星的谱线强度测得,视星等可直接观测到。因此,依据距离d与绝对星等M和视星等m之间的关系:只要测出同一天体的视星等和绝对星等,就可以确定其距离。
用分光视差法可以测定100秒差距(pc)以外的恒星的距离,这种方法要拍摄恒星的光谱,当恒星距离超过100千秒差距(pc)时,难以拍到它们的光谱,因而也就无从知道它们的准确光度,无法测定其距离了。
3.谱线红移测距法
用谱线红移法可以测定远达百亿光年范围的距离。
光谱早在17世纪就已经发现,阳光透过棱镜会在后面的屏幕上产生一条七色彩带,牛顿称其为光谱。通过对天体光谱的分析,不仅可以知道它们的化学组成,还能推知许多物理性质。用来对天体作光谱观测的装置叫天体摄谱仪。20世纪初,有人发现除少数几个较近的星系外,几乎所有的星系光谱都有红移。所谓红移是指当天体远离我们而去时,天体光谱线向长波端(红端)移动,即观测到的谱线比实验室测知的相应谱线的波长较长;相反,如果天体的运动是向我们而来,谱线就向短波端(蓝端)位移,称为蓝移。1929年,哈勃发现:星系距我们越远,其谱线红移量越大。
此式被称为哈勃定律,式中Z为红移量,c为光速,r为距离,H为哈勃常数,目前定为H=50~80千米/(秒·兆秒差距)。
根据哈勃定律,只要测出河外星系谱线的红移量Z,便可算出星系的距离d。
天体距离的测量方法除以上简要介绍的几种外还有许多,在实际观测中,人们根据天体的实际情况选择不同的测量方法。随着科学技术的进步,将会有更多的先进方法用于天体测量中,天体到地球的距离测量精度也将不断提高。教师在教学过程中可鼓励学生积极探索天体测量方法。
