特殊复合球铰 3-RPS并联机构及其连续刚度模型
2010-03-16崔学良韩先国陈五一
崔学良 韩先国 陈五一
(北京航空航天大学 机械工程及自动化学院,北京 100191)
特殊复合球铰 3-RPS并联机构及其连续刚度模型
崔学良 韩先国 陈五一
(北京航空航天大学 机械工程及自动化学院,北京 100191)
采用矢量微分法研究了在大载荷作用下,兼顾支链和铰链刚度以及雅克比矩阵变化等影响因素的 3-RPS并联机构完整连续刚度模型.基于螺旋理论分析了 3-RPS并联机构支链及铰链构件所受作用力与机构外载荷之间的力平衡关系.采用矢量微分法分析了 3-RPS并联机构动平台位姿变化与支链及铰链构件变形之间的关系.采用矢量微分法对机构的力学平衡方程进行微分,建立了完整的连续刚度模型,最后进行了数值模拟分析,结果表明并联机构刚度受载荷和位姿变化影响,简化刚度模型与完整刚度模型在工作空间边界处差值较大.
连续刚度模型;雅克比矩阵;复合球铰;螺旋理论;矢量微分法
3-RPS并联机构结构简单、控制相对容易,在加工制造领域中具有良好的应用前景.但在高速、重载的工况下,并联机构各构件弹性变形增大,且由于铰链间隙无法有效补偿,从而导致其整体刚度变弱,因此兼顾支链和铰链的弹性变形,对并联机构的整机刚度进行分析和补偿有十分重要的意义.文献[1]建立了并联机构末端操作力与末端变形的映射模型.文献[2]推导了 Stewart平台的刚度矩阵,计算了其最大、最小刚度的方向及数值.文献[3]给出了并联机床各支链等效刚度及载荷的确定方法.文献[4]利用虚功原理分别求解了并联机床各子系统的刚度,然后用线性叠加求得其整体刚度.文献[5]针对过约束并联机构也做了类似的工作.
以上对并联机构刚度的研究中,都是将机构的雅克比矩阵看作是与其结构参数和位姿有关的常量矩阵.但在大载荷作用下,并联机构位形改变,从而导致雅可比矩阵发生变化,因此其刚度模型还与外载荷有关.文献[6-7]利用矢量法建立了考虑雅克比矩阵变化的 Stewart并联机床瞬时刚度模型,但推导过程不甚清晰,所得结果难以推广应用.文献[8]利用虚功原理建立了并联机构的完整连续刚度模型,但文中将被动关节的产生力矩与主动关节的产生力矩等同对待,在对被动铰链作用力的计算时仍有些不便.本文针对大载荷和大姿态要求的工况,设计了一种具有特殊复合球铰的 3-RPS并联机构,并对其整个工作空间中的刚度进行了分析,建立机构的连续刚度模型完整的计算公式,从而为并联机构精确刚度补偿奠定基础.
1 并联机构及复合铰链的结构特性


图1 并联机构复合铰链

图2 并联机构动平台
如图 3所示,在静平台上建立参考坐标系 OXYZ,理想动平台平面由 3个复合球铰的球心Pi(i=1,2,3)确定,建立动坐标系 P-xyz,原点 P位于△P1P2P3中心.

图3 改进的 3-RPS并联机构示意图
2 并联机构力平衡分析
力平衡分析是并联机构刚度模型建立的基础.如图 4所示,3-RPS并联机构的受力平衡方程:

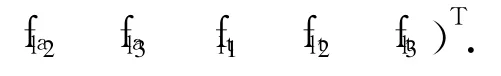

图4 3-RPS并联机构整体受力分析

式中,F为机构所受外载荷;Srai(i=1,2,3)为沿转轴)轴向作用力 6维单位线矢;Srni为沿支链矢量 li与转轴矢量的公法线方向上的 6维单位力线矢;Sroi为沿上面两矢量的公法线方向上6维单位力线矢;frai,frni和froi(i=1,2,3)为式(1)所得支链作用力线矢 flai,flti(i=1,2,3)沿上述矢量方向投影值.

图5 动平台及转轴结构体受力分析
受作用力共有 9个分量,为建立并联机构整体刚度模型,需将其合并为 6个分量.由螺旋相关性[10]可知,作用在轴)上的两个力矢 frniSrni和 froiSroi(i=1,2,3)位于其法平面内,可将其合并为一个力矢:



3 构件弹性变形与机构位姿偏移
并联机构的刚度模型实质上是动平台位姿偏移与其所受外载荷之间的关系.为确定这一关系模型,需考察支链 li(i=1,2,3)及复合铰链转轴)弹性变形与机构动平台位姿偏移之间的几何关系.由位置逆解模型可知,并联机构在变形前满足几何约束方程:

式中,Bi(i=1,2,3)为 3-RPS并联机构静平台上转动副 ui(i=1,2,3)的中点坐标,参见图 3;PPi(i=1,2,3)为复合球铰球心坐标在动坐标系中的表示;P为动坐标系原点在参考坐标系中的坐标;T为动平台姿态矩阵.
当机构受载变形后,姿态矩阵由 T变为 T+δT,其中 δ为微分算子,以下同.并联机构变形后的几何约束方程为

式中,δli(i=1,2,3)为支链 li在外作用力下的弹性变形;PPi+PδPi(i=1,2,3)为并联机构变形后复合铰链中心位置在动坐标系中的表示.
由机器人机构学[11]等效转轴理论,动平台姿态的偏移量 δT可等效为动坐标系绕过其原点的某一转轴转过一个微小角度 δθ.将式(7)减去式(6),可得

忽略高阶无穷小量,有

式中,PδPi=Pδsai+Pδsti(i=1,2,3)为复合铰链的中心位置偏移量,其中Pδsai和Pδsti分别为轴)轴向和侧向弹性变形量在动坐标系中的表示.式(9)两端分别点乘 lai和 lti(i=1,2,3)方向上的单位矢量,经整理可得并联机构动平台位姿偏移与支链 li(i=1,2,3)及复合铰链转轴弹性变形之间的几何约束方程:式中,δl为一由各支链轴向和侧向弹性变形大小所构成的矢量,δl=(δla1δla2δla3δlt1δlt2为轴)弹性变形在支链 li矢量方向上的映射矩阵;δs为轴轴向和侧向弹性变形量大小所构成的矢量;δD为动平台位姿偏移量,δD=(δPTδθT)T.


4 并联机构完整连续刚度模型
并联机构刚度与位姿和载荷有关,在大载荷作用下,尤其在工作空间的边界处,并联机构受载前后雅可比矩阵发生变化,即有 δJfl≠0.对式(1)全微分,并考虑到支链 li(i=1,2,3)的受力变形关系 δf1=-k1δl,可得

式中,Jfl为并联机构的力雅可比矩阵;k1为一由支链 li(i=1,2,3)轴向刚度和侧向刚度所组成的6维对角阵;

当雅克比矩阵 Jfl非奇异时,可得支链 li(i=1,2,3)弹性变形与动平台位姿偏移量之间的关系:

式中,K为并联机构的整体刚度矩阵.

式中

由式(10),并参考式(12)和式 (13),有



lh联机构的整机连续刚度模型.当忽略雅克比矩阵变化对机构整体连续刚度的影响时,式(16)可简化为

式中,K1为仅考虑支链刚度时并联机构的简化整体刚度模型.
5 数值模拟
为了形象地观察并联机构完整刚度模型和简化刚度模型对机构刚度性能评价的差异,本文分别计算机构在相同载荷作用下采用完整刚度模型所得机构末端位姿偏移量与采用简化刚度模型所得末端位姿偏移量,通过比较两组结果得出并联机构不同刚度模型对其刚度性能进行评判的差异.3-RPS并联机构样机结构如图 6所示.结构参数如表 1所示.样机采用卧式放置,动平台上装有操作头,加工时工作载荷垂直于动平台平面.

图6 3-RPS并联机构样机模型

表 1 3-RPS并联机构的参数
设操作头自重为 6 kN,加工作业时工作载荷为 2kN.为衡量并联机构的整体刚度,本文分析并联机构在外载荷作用下动平台位姿的偏移量.分别由式(15)的完整连续刚度模型和式(17)简化刚度模型分析动平台在加载过程中的位姿偏移量,结果如图 7~图 10所示.图 7和图 8所示为并联机构在章动角为 45°,进动角为 120°,动 、静平台 z向距离在 0.8~1.8m变化时动平台的位姿偏移曲线.图9和图10所示为机构在动、静平台 z向距离为 0.8m,章动角为 45°,进动角 0~360°变化范围内动平台的位姿偏移量曲线.
由图 7~图 10可看出,在计算动平台的位姿偏移量时,采用简化刚度模型的计算结果小于采用完整刚度模型的计算结果,表明采用简化刚度模型分析所得的并联机构整机刚度较大.如图 9所示,在静平台 z向距离为 0.8m,章动角为 45°,进动角为 90°处,采用简化刚度模型求得的动平台位置偏移量为 0.98mm,而采用完整刚度模型求得的动平台位置偏移量为 1.8mm.在该位姿处动平台的角度偏移量相差为 0.4°,如图 10所示.这是由于在大载荷作用下,机构发生变形,而简化刚度模型中雅可比矩阵是以变形前的位形参数计算的,因此采用简化刚度模型计算动平台位姿偏移量时,会产生较大的误差.完整连续刚度模型考虑到载荷对机构变形的影响,由此模型计算所得的动平台位姿偏移量更接近实际,有利于对由机构刚度变形引起的位姿误差作出合理补偿.
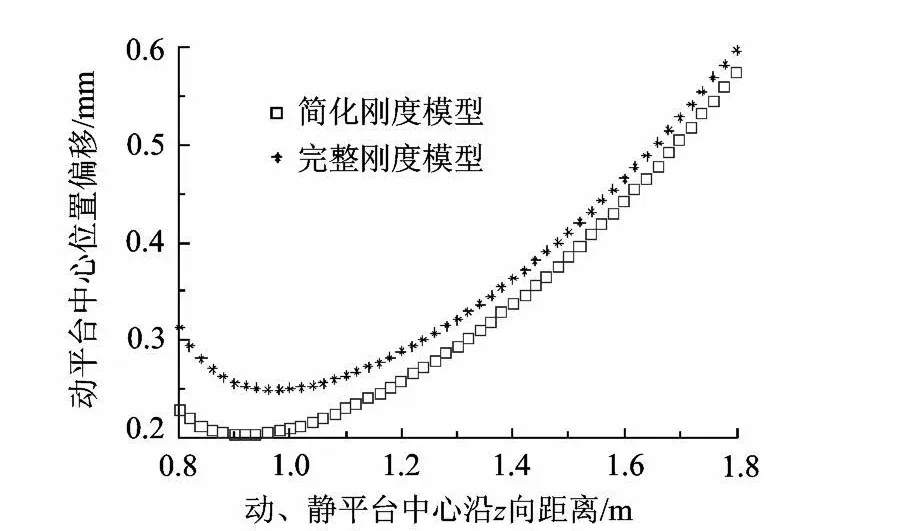
图7 加载过程中动平台中心位置偏移量

图8 加载过程中动平台姿态角偏移量

图9 两种刚度模型的动平台中心位置偏移量

图10 两种刚度模型的动平台姿态角偏移量
6 结 论
1)并联机构的整机刚度与所受外载荷和动平台的位姿参数有关;
2)并联机构的整机刚度主要受支链刚度与铰链刚度的共同影响;
3)在大载荷的作用下,尤其当并联机构动平台运动在工作空间边界处时,由简化刚度模型与完整刚度模型所求得的机构动平台位姿偏移量差值较大,最大差值甚至相差 1倍.
References)
[1]Gosselin C.Stiffness mapping for parallel manipulators[J].IEEE Transactions on Robotics and Automation,1990,6(3):377-382
[2]EI-Khasawneh B S,Ferreira P M.Computation of stiffness and stiffness bounds for parallel link manipulators[J].International Journal of Machine Tools&Manufacture,1999,39(2):321-342
[3]王世军,黄玉美.并联机床支链刚度及载荷的确定方法[J].西安理工大学学报,2004,20(2):117-121 Wang Shijun,Huang Yumei.Determination method of branch stiffness and load for parallel machine tool[J].Journal of Xi'an University of Technology,2004,20(2):117-121(in Chinese)
[4]Huang Tian,Zhao Xingyu,Whitehouse D J.Stiffnessestimation of a tripod-based parallel kinematic machine[J].IEEE Transactions on Robotics and Automation,2002,18(1):50-58
[5]Anatol P,Damien C,Philippe W.Stiffness analysis of overconstrained parallel manipulators[J].Mechanism and Machine Theory,2009,44(5):966-982
[6]陈吉清,兰凤崇.Stewart并联机构瞬时刚度分析与应用[J].南京理工大学学报,2007,31(4):482-486 Chen Jiqing,Lan Fengchong.Instantaneous stiffness analysis and application in Stewart parallel machine tools[J].Journal of Nanjing University of Science and Technology,2007,31(4):482-486(in Chinese)
[7]Chen J,Lan F.Instantaneous stiffness analysis and simulation for hexapod machines[J].Simulation Modelling Practice and Theory,2008,16(4):419-428
[8]赵铁石,赵延治,边辉,等.空间并联机构连续刚度非线性映射[J].机械工程学报,2008,44(8):20-25 Zhao Tieshi,Zhao Yanzhi,Bian Hui,et al.Continuous stiffness nonlinear mapping of spatial parallel mechanism[J].Chinese Journal of Mechanical Engineering,2008,44(8):20-25(in Chinese)
[9]曾宪菁.球面并联机构运动学设计理论与方法[D].天津:天津大学机械工程学院,2001 Zeng X ianjing.The kinematics design of spherical parallel manipulator[D].Tianjin:School of Mechanical Engineering,Tianjin Unversity,2001(in Chinese)
[10]黄真,赵永生,赵铁石.高等空间机构学[M].北京:高等教育出版社,2006:29-30 Huang Zhen,Zhao Yongsheng,Zhao Tieshi.Advanced spatial mechanism[M].Beijing:Higher Education Press,2006:29-30(in Chinese)
[11]蔡自兴.机器人学[M].北京:清华大学出版社,2000:66-72 Cai Zixing.Robotics[M].Beijing:Tsinghua University Press,2000:66-72(in Chinese)
(编 辑:文丽芳)
Continuous stiffness modeling o f3-RPS parallel kinematic machine with special composite spherical joints
CuiXueliang Han Xianguo Chen Wuyi
(School of Mechanical Engineering and Automation,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)
A comprehensive continuous modeling methodology of3-RPS parallel machine under dynamic load condition was developed and presented by considering the stiffness of legs and joints.The variational Jacobian matrix was used through vector differential and equivalent mechanism technique.Based on the screw theory,the force equation between the dynamic load on the mobile platform and its reaction forces on the legs and joints of the 3-RPS parallel machine was investigated and analyzed.The relationship between the pose(position and orientation)distortion of the mobile platform and the elastic deformation behavior of the legs and joints on 3-RPS parallel machine was established and analyzed by vector differential.A comprehensive dynamic stiffness model of the machine was developed by adding the total differential of the residual forces on the machine system.To validate the methodology,a numerical simulation was carried out.The result shows that the stiffness model of the parallel machine is affected by the outside load and the pose of the mobile platform.There is a large difference between the simple stiffness model and the integrate stiffness model near the workspace boundary of the parallel machine.
continuous stiffness model;Jacobian matrix;composite spherical joint;screw theory;vector differential method
TP 242
A
1001-5965(2010)11-1275-06
2010-01-28
航空科学基金资助项目(20081651025);北京市重点实验室资助项目
崔学良(1971-),男,山西长治人,博士生,cuixueliangsj@163.com.
