天线罩干扰下的雷达 /红外复合导引头数据融合

曹晓瑞 董朝阳 王 青 陈 宇

(北京航空航天大学 自动化科学与电气工程学院,北京 100191)

天线罩干扰下的雷达 /红外复合导引头数据融合

曹晓瑞 董朝阳 王 青 陈 宇

(北京航空航天大学 自动化科学与电气工程学院,北京 100191)

针对雷达/红外复合导引头中存在天线罩折射以及外部干扰问题,在三维模型下,提出一种基于扩展卡尔曼滤波(EKF,Extended Kalman Filter)的多模型算法,对天线罩斜率进行估计,并将估计结果代入 EKF,降低观测视线角中的天线罩折射干扰,形成最优局部估计.采用基于环境信息的加权因子法对雷达/红外局部估计结果进行融合,通过环境信息度量传感器测量结果的可信度,忽略不可信的局部估计结果.设计 4组算例检验融合算法性能,仿真结果表明:所提算法可以准确估计天线罩斜率,合理并有效使用雷达/红外传感器信息,提高系统估计精度.

复合制导;数据融合;天线罩;扩展卡尔曼滤波

为了适应日益复杂的攻防对抗环境,现代导弹一般采用复合制导方式提高命中精度和抗干扰能力.雷达/红外作为典型的异类传感器系统,可以实现信息互补,改善目标跟踪性能,提高系统的生存能力,因而引起了广泛关注.

已有雷达/红外复合制导、数据融合研究文献中,观测方程中一般不考虑天线罩折射角,认为天线罩误差已在传感器内进行补偿.目前常用的极化补偿法和电气补偿法,由于受到工艺和数据的限制,很难满足现代制导系统对天线罩性能的要求[1-2],实际系统应用中,导引头输出信号仍然包含天线罩误差,需要在融合滤波中对其进行估计补偿.

利用雷达/红外的冗余特性提高系统的制导精度一直是数据融合研究的热点.文献[3-4]分别利用小波神经网络和模糊逻辑设计融合算法,提高融合系统的抗干扰性,保证整体估计精度.但此类算法结构复杂,计算量大,不适用于时效性和可靠性要求较高的弹载制导系统.因此如何设计一种结构简单,可靠性高的融合算法,成为复合制导工程应用中急需解决的问题.

本文针对考虑天线罩折射以及外部干扰的雷达/红外复合制导系统,提出了一种基于扩展卡尔曼滤波(EKF,Extended Kalman Filter)的天线罩误差多模型估计算法,降低天线罩干扰;在此基础上,设计基于环境信息的加权因子融合算法,合理利用雷达/红外传感器观测信息,得到高可信的目标跟踪信息.

1 滤波模型

1.1 状态方程

在惯性坐标系中建立弹目相对方程:

其中,r(t)=[x(t),y(t),z(t)]T为弹目相对位置向量;v(t)=[x·(t),y·(t),z·(t)]T为弹目相对速度向量;aM(t)=[aMx(t),aMy(t),aMz(t)]T和分别为导弹、目标加速度沿惯性坐标系 3轴的投影向量.

为简化起见,将导弹自动驾驶仪闭环回路等效为一阶延时,其状态方程可表示为

其中,ac(t)=[acx(t),acy(t),acz(t)]T为加速度指令;ωM(t)=[ωMx(t),ωMy(t),ωMz(t)]T为零均值高斯白噪声,其方差阵为 QM(t);AM=diag(-1/τMx,-1/τMy,-1/τMz),τMx,τMy,τMz为导弹控制系统时间常数;BM=-AM.

采用 Singer模型对目标机动进行建模[5]:

其中,AT=diag(-1/τTx,-1/τTy,-1/τTz),τTx,τTy,τTz为目标机动时间常数;ωT(t)=[ ωTx(t),ωTy(t),ωTz(t)]T为零均值高斯白噪声,其方差阵为QT.

综上所述,得到系统线性动力学状态方程:

其中

其方差阵为 Q.

1.2 红外观测方程

红外传感器只获取角信息,且不受天线罩影响,其观测方程为

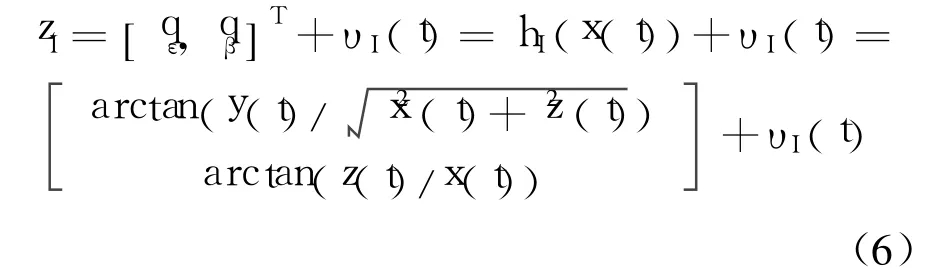
其中,qε,qβ为两 方向视线角;υ·

I(t)=[ υIε(t),υIβ(t)]T为零均值高斯白噪声,其方差阵为RI(t).

1.3 考虑天线罩误差影响的雷达观测方程

假设导弹滚转通道稳定,受天线罩折射影响,雷达测得的视线角为[5]

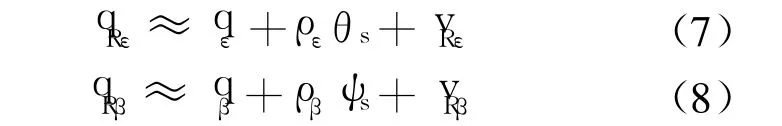
其中,θs=qε-θM,ψs=qβ-ψM,θM,ψM为导弹弹体姿态角;ρε=∂fε/∂θs,ρβ=∂fβ/∂ψs分别为俯仰、偏航两平面内天线罩误差斜率.依此可以得到考虑天线罩误差的雷达观测方程:

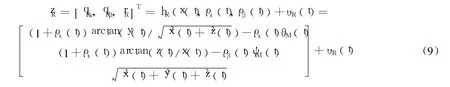
其中,rR为测量弹目相对距离;υR(t)=[υRε(t),υRβ(t),υRr(t)]T为零均值高斯白噪声 ,其方差阵为RR(t).

2 传感器滤波算法与航迹融合算法

数据融合总体结构如图 1所示.利用传感器输出 zI,zR和全局状态一步预测值及其协方差阵x^(k|k-1),P(k|k-1),产生局部估计结果.其中x^R(k|k),PR(k|k)表示雷达局部估计值及其协方差阵,)表示红外局部估计值及其协方差阵,PRI(k|k)为两传感器的相关估计方差,且.同步处理后将局部估计结果送至融合中心进行航迹融合,得到全局估计值及其协方差阵

图1 雷达/红外数据融合结构图

2.1 考虑天线罩误差的雷达多模滤波算法

利用最优估计理论解决天线罩误差干扰一直被国内外学者所关注.文献[5]通过地面信号修正滤波结果,给出了一种新的滤波补偿思路,其所提方法存在如下缺点:①在斜率估计过程中,需要利用地面雷达信息对在线估计结果进行修正,对于大部分自寻的导弹而言,这种信息是无法得到的;②这种滤波结构由 N个大维数的卡尔曼滤波器构成,总体计算量大,估计延时大,影响系统的补偿效果.本文在文献[5]的基础上,提出一种基于 EKF的多模滤波算法,对天线罩误差斜率进行估计.

按照多模滤波思想,假定天线罩斜率在一组可能的取值中发生跳变,其跳变概率服从马尔科夫过程,具体数学表示如下所示:

其中,ρεp,ρβq为两平面天线罩斜率的可能取值.将式(10)进行合并,构成三维天线罩斜率组模型:

其中,ρi的总数 N=nm.

利用 ρi和状态预测值 x^(k|k-1),构建 N个k时刻的伪观测量

与之相对应的观测新息和协方差阵表示为

利用式(13)、式(14)所得结果,更新 k时刻的似然函数:

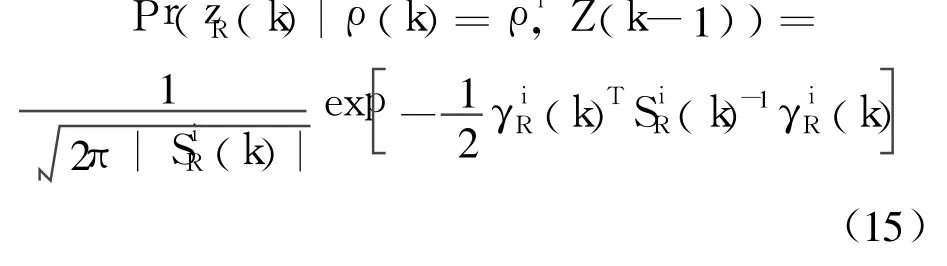
其中,Z(k-1)={zR(k-1),…,zR(1)}为观测量序列.

依照马尔科夫状态转移方法,可以计算出 k时刻对应于斜率模型 ρi的模型概率为

其中,Prj(k-1)为 k-1时刻对应于斜率模型 ρj的模型概率 ;θij≜Pr(ρ(k)=ρi|ρ(k-1)=ρj)为状态转换概率,可以通过构造马尔科夫转移矩阵得到;Λ为归一化因子,表达式为

依据模型概率,斜率估计结果可以表示为

将天线罩斜率估计值代入标准的 EKF进行滤波,得雷达局部估计结果.具体计算公式为

其中,γR(k),SR(k)为观测新息及其协方差阵;KR(k)为卡尔曼滤波增益;HR(k)为非线性函数hR(x)在)处的线性化表达式:

2.2 基于 EKF的红外滤波算法

利用红外观测量 zI和状态预测结果1),P(k|k-1)进行 EKF滤波,得到红外局部估计结果

2.3 航迹融合算法

雷达红外局部估计结果融合过程中,利用环境变量描述传感器数据的可用性,定义环境变量[3]为

假设 γ∈Rl,则 η理论上服从自由度为 l的χ2分布.按照 χ2分布规律,设定阈值 Δ,定义不同置信水平上的传感器有效域:如果 η≥Δ,传感器测量不可信,在融合过程中忽略该传感器的信息;如果 η＜Δ,传感器测量可信,在融合过程中采用该传感器的信息.对于雷达传感器,其测量值包括弹目相对距离和两方向视线角,l=3,考虑 95%的置信水平,ΔR=7.8;对于红外传感器,其测量值为两方向视线角,l=2,考虑 95%的置信水平,ΔI=5.9.

在环境变量计算的基础上,利用加权因子法融合两传感器估计结果:

其中,αR,αI分别为雷达、红外加权因子,具体计算公式根据环境变量的不同而不同:

1)如果 ηR＜7.8,ηI＜5.9,则两传感器信息都可用:

2)如果 ηR＜7.8,ηI＜5.9,则红外信息不可用,融合输出为雷达估计结果,αR=1,αI=0;

3)如果 ηR≥7.8,ηI＜5.9,则雷达信息不可用,融合输出为红外估计结果,αR=0,αI=1;

4)如果 ηR≥7.8,ηI≥5.9,则两传感器信息都不可用,融合输出为状态预测结果.

3 仿真验证

本节通过数学仿真,验证所提算法的有效性.仿真初始条件如下:惯性坐标系下,导弹初始位置(3km,1km,0),初始速度(400m/s,100m/s,0);目标初始位置(15 km,5 km,-3 km),初始速度(-200m/s,0,0).导弹闭环控制时间常数 τMx=τMy=τMz=0.1 s,噪声方差阵 QM=diag(qM,qM,qM),qM=10-5m2/s4.目标机动时间常数 τTx=τTy=τTz=0.5 s,噪声方差阵 QT=diag(qT,qT,qT),qT=10-4m2/s4.雷达传感器测量噪声方差阵RR=diag(εεR, εβR, εr),其中 εεR=εβR=4 ×10-4rad2,方差 εr=1m2;红外传感器测量噪声方差阵 RI=diag(εεI,εβI),其中 εεI=εβI=10-4rad2.用正弦函数模拟加入的天线罩误差斜率.

通过 4个仿真算例测试所提算法的估计精度和抗干扰能力,4个算例都加入雷达天线罩折射,其中算例 1采用标准加权因子法,不对天线罩误差进行建模估计;算例 2按本文提出算法,对天线罩斜率进行估计后再进行航迹融合.图 2给出了算例 1、算例 2的弹目相对位置估计误差结果.由图可以看出,由于雷达观测信息受天线罩干扰,算例 1的估计误差较大,且误差大小随天线罩斜率变化而变化;算例 2中所提多模型估计算法可以对两方向雷达天线罩斜率进行有效估计(如图 3所示),在此基础上,再进行制导滤波和航迹融合,整体估计精度较高.

图2 算例 1、算例 2位置估计误差曲线

图3 算例 2天线罩斜率估计结果示意图

为了验证融合算法的抗干扰性,在算例 2的基础上,假设在 10～13 s间,红外传感器受到干扰,测量噪声方差增大 10倍,雷达观测信息不变.算例 3采用标准的加权因子法,算例 4采用本文所提算法.由图 4可以看出,0～10 s中,两传感器测量信息都可用,两种融合算法估计误差相同;10～13 s过程中,由于红外测量信息受到干扰,算例 3估计误差变大;本文所提算法通过观测环境变量判断干扰情况,在此期间舍弃红外传感器信息,估计精度高于算例 3;当干扰消除 3s后,算例 3的结果收敛到与算例 4结果基本相同.

图4 算例 3、算例 4位置估计误差曲线

4 结束语

本文针对雷达/红外复合制导导引头,提出了一种考虑天线罩误差干扰的数据融合整体方案,依据本次仿真条件下所得结果,可以得出以下结论:①雷达天线罩影响导引头测量精度,如果不对其进行估计,融合估计误差大,误差具体量值与天线罩误差相关;②所提多模滤波算法可以对天线罩斜率进行有效地估计,提高融合系统整体估计精度;③所提融合算法可以对传感器局部估计结果进行自检测,剔除可信度低的传感器信息,保证融合系统整体估计精度.

References)

[1]宋银锁.空空导弹天线罩发展展望[J].航空兵器,2005,3(6):19-23 Song Yinsuo.Development prospect of radome for air-to-air missile[J].Aero Weaponry,2005,3(6):19-23(in Chinese)

[2]Bhattacharyya A.In flight radome error compensation through simulated test data[R].AIAA-2005-6454,2005

[3]原泉,董朝阳,王青.基于小波神经网络的多传感器自适应融合算法[J].北京航空航天大学学报,2008,34(11):1331-1334 Yuan Quan,Dong Chaoyang,Wang Qing.Adaptive fusion algorithm based on wavelet neural networks for multisensor measurement[J].Journal of Beijing University of Aeronautics and Astronautics,2008,34(11):1331-1334(in Chinese)

[4]Loebis D,Sutton R,Chudley J,et al.Adaptive tuning of a Kalman filter via fuzzy logic for an intelligent AUV navigation system[J].Control Engineering Practice,2004,12(12):1531-1539

[5]Taek L S,Sang JS.Active hom ing performance enhancement with multiple model radome slope Estimation[R].AIAA-2004-4899,2004

(编 辑:刘登敏)

High accuracy data fusion of radar/in frared multi-mode guidance seeker with radar radom e interference

Cao Xiaorui Dong Chaoyang Wang Qing Chen Yu

(School of Automation Science and Electrical Engineering,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)

In order to improve anti-interference ability of radar/infrared multi-pattern composite guidance seeker with radome refraction,a new multiple model radome slope sestimate algorithm based on extended Kalman filter(EKF)was proposed in the three dimensional engagement scenarios.The slopes estimates were utilized in EKF to degrade the radome refraction in measuring line-of-sightand to get the localoptimalestimates.Both of partial estimation results were integrated with sensor weighted coefficients depended on the sensor contextual information,which was introduced to characterize the reliability of sensor.The invalidity signals would be rejected.The performance of the proposed fusion algorithm was examined by four examples.Simulation results show that the algorithm can appropriately use radar/infrared measurement with radome slopes effectively estimating to enhance the estimating accuracy.

composite guidance;data fusion;radome;extended Kalman filter

TJ 765

A

1001-5965(2010)11-1290-05

2009-10-12

曹晓瑞(1981-),男,山西怀仁人,博士生,caoxr1981@gmail.com.