基于盲源分离技术的航空发动机振动信号分析
2010-03-16秦海勤徐可君
秦海勤 徐可君
(海军航空工程学院青岛分院 航空机械系,青岛 266041)
欧建平
(海装航空技术保障部,北京 100071)
基于盲源分离技术的航空发动机振动信号分析
秦海勤 徐可君
(海军航空工程学院青岛分院 航空机械系,青岛 266041)
欧建平
(海装航空技术保障部,北京 100071)
基于双转子航空发动机机匣拾取振动信号特征的分析,采用基于数学形态学滤波前处理的盲源分离识别方法进行特征提取.针对机匣拾取振动信号的特征,利用开—闭和闭—开组合数学形态滤波器在保留信号基本形状的前提下,滤除掉原始信号中的噪声分量.利用 Fast ICA算法恢复高、低压转子源振动信号的波形.对实测数据的分析表明,该方法能够较好地恢复高、低压转子所激振动信号的频域结构信息,有利于提高故障定位的准确性.
航空发动机;双转子;盲源分离;故障定位;振动信号分析
现代高性能先进的涡喷、涡扇发动机大部分以同心轴的高、低压双转子系统为主要结构形式,因此,其振动形式与一般单转子的旋转机械有所差异.但囿于发动机自身安装空间的限制,目前很难对高、低转子分别进行振动监测.通用的做法是通过安装在机匣上的传感器进行拾振,所测得的振动信号主要是高、低压转子振动信号的混叠,只能部分满足振动监测的需要,故障时,若信号频谱结构比较复杂,尤其是出现次谐波等低倍频分量时,很难确定是高压转子引起的振动还是低压转子引起的振动,增加了故障诊断的难度.
为了提高航空发动机振动状态监测和故障诊断的准确性,基于双转子航空发动机机匣拾取振动信号的特征,本文采用基于数学形态学滤波前处理的盲源分离识别方法,对实测发动机振动信号进行了分析.结果表明,该方法能够较好地恢复高、低压转子源振动信号的波形特征,能够进一步提高故障定位的准确性.
1 双转子航空发动机振动信号特征
航空发动机结构系统非常复杂,其振动信号既包括高压转子系统的振动,又包括低压转子系统的振动,也包括各种轴承、齿轮、导管、泵等结构件的振动.但由于高、低压转子的质量较轴承、齿轮等的质量大许多,且高、低压转子运行在高速状态下,同时轴承、齿轮等零部件激起的高频冲击信号在到机匣的传递过程中衰减较大.因此,发动机机匣很多部位拾取的振动信号以高、低压转子的振动为主,其余部件的振动能量相对较小.所以,根据一般旋转机械的振动信号特征[1],双转子发动机机匣振动信号可以近似表示为

式中,shigh,slow为高、低压转子的振动信号;fhigh,flow为高、低压转子的转动频率;Ai,Ci为高、低压转子第 i阶倍频对应的幅值;ai,ci为高、低压转子第 i阶倍频对应的初始相位;Bi,Di为高、低压转子次谐波对应的幅值;τi,λi为高、低压转子次谐波相对于各自工频的比例系数,τi<1,λi<1;bi,di为高压转子次谐波对应的初始相位;o(t)为噪声及其他低能量的高频信号.
发动机工作时,高、低压转子分别以不同的转速运行,因此,在转速已知的情况下,通过 FFT变换容易识别出高、低压转子的工频和倍频分量,但对于次谐波分量却很难区分究竟是由高压转子振动还是由低压转子振动引起.尤其对于发动机振动信号,其实际采样方式常常以高压转子的转速为整周期进行采样.对于所得阶次域信号,区分次谐波分量更加困难.图 1为某型双转子发动机台架试车发生故障时通过涡轮机匣拾取的振动信号高压阶次谱.
图1所示是以高压转速为整周期的阶次谱,此时高压转速为 11 095 r/min,对应低压转速为6787r/min,由图 1可以非常容易区分出高压转子的 1倍工频和低压转子的 1倍频和 2倍频(由于低压转速与高压转速的比值为 0.6左右,因此,在以高压转速为整周期的阶次谱中,低压 1倍工频的横坐标在 0.6附近,2倍频的横坐标在 1.2附近).但对于图 1中横坐标为0.3附近的次谐波分量,究竟是低压的 0.5倍次谐波分量,还是高压自身的 0.3倍次谐波分量却无法区别.

图1 某型发动机振动信号高压阶次谱
盲源分离技术基于一定的假设,通过一定的处理手段能够从多个独立源的混叠信号中把各独立源分离出来.双转子发动机高、低压转子运行转速不同,故可以作为两个独立的信号源,因此,通过盲源分离技术应该能够识别出高、低压转子的振动信号.但常用的分离算法大都建立在瞬时混叠无噪模型的基础之上,而通过机匣拾取的振动信号,既包含噪声信号又包含小量的高频冲击信号,因此,在利用盲源分离技术之前必须进行前处理.传统的滤波方法如小波变换等对白噪声滤波效果较好,但无法滤掉轴承、齿轮等的高频冲击信号,同时小波变换自身对噪声和微弱信号也比较敏感.而基于积分几何和随机集论建立的数学形态滤波方法不但比传统的滤波更为有效,而且对于原始信号发生严重畸变并伴有较强噪声的情况仍能很好地识别其基本形状[2-3].为此,本文提出如下基于数学形态滤波前处理的盲源分离识别框架.
2 基于数学形态学前处理盲源分离
2.1 识别框架
图2为双转子发动机基于数学形态学前处理的盲源分离识别框架(其中,和分别表示滤波处理后的高、低压转子信号,而和分别表示盲源分离后所得高、低压转子信号).即对于从发动机机匣采集的振动信号首先通过数学形态学滤波器滤除掉不关心的噪声和高频脉冲信号等,以保持高、低压转子振动信号的基本形状,然后通过盲源分离矩阵识别出高低压转子的振动.

图2 基于数学形态学前处理的盲源分离识别框架
2.2 数学形态学基本原理
数学形态学借助于集合来描述信号,即将原始信号 x(n)看成为定义在 X=(0,1,2,…,N-1)上的离散函数.同时定义结构元素 g(n)为 G=(0,1,2,…,M-1)上的离散函数,且 N≥M.利用结构元素 g(n)对原始信号 x(n)进行“探测”,则x(n)关于 g(n)的腐蚀和膨胀分别定义为

而 x(n)关于 g(n)的开、闭运算分别定义为

开运算使目标轮廓光滑,能够去掉毛刺和孤立点,可抑制信号中的正脉冲噪声;闭运算可以填平小沟、弥合孔洞和裂缝,可滤除信号中的负脉冲噪声.为了同时滤除信号中的正、负噪声,常采用开、闭运算的级联形式.根据开、闭运算的不同级联形式,形成了形态开—闭和闭—开滤波器.
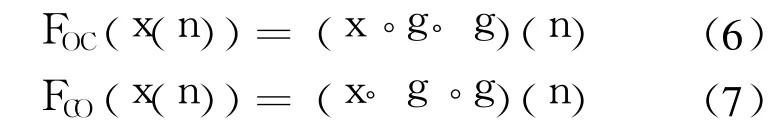
在实际应用中,为了有效抑制信号中的各种噪声,常常采用开—闭和闭—开组合形态滤波器进行滤波:

另外,结构元素的选择对信号处理结果也有较大影响.但对于振动信号的处理,三角形、圆形、直线形 3种形状的结构元素可取得较好的滤波效果[2].
2.3 盲源分离基本原理
盲源分离[4]最常用的方法之一是独立分量分析(ICA,Independent Component Analysis).假定共有N个传感器拾取到 N个观测信号 xi,i=1,2,…,N,每个观测信号由 M个独立源信号 si(i=1,2,…,M)的线性组合 X=A·S而成.其中,X=[x1,x2,…,xN]T和 S=[s1,s2,…,sM]T分别是混合信号矢量和源信号矢量,A是 N×M的未知混合矩阵(要求 N≥M).问题的难点在于信号源 S和混合矩阵 A未知的情况下,如何找到一个分离矩阵 B,把相互独立的源信号从混合信号中分离出来.基于不同的独立性判决准则,形成了不同的分离算法.其中应用较为广泛的是基于负熵的快速 ICA算法——Fast ICA.
由中心极限定理可知,由许多相互独立的随机量之和组成的任一随机量,只要各独立随机量具有有限的均值和方差,不论各独立随机量为何种分布,则该随机量必接近高斯分布.Fast ICA算法正是通过对分离结果的非高斯性度量来监测分离结果之间的相互独立性,当各分离结果的非高斯性达到最大时,表明已完成了对各独立分量的分离.对于非高斯性的度量,通过式 (9)进行度量:


Fast ICA算法的具体过程[5-6]为:
1)对 x去均值,并进行白化处理得 z,即E(z·zT)=I;
2)确定独立分量数目 M,随机选择模为 1的初始向量 bi,组成 B=[b1,b2,…,bM];
5)若 B不收敛,则返回步骤 3).
得到分离矩阵 B后,即可求得各独立源 S=A-1X=BX.
3 应用实例
某型双转子航空发动机在台架测试时安装有3个测振点,分为前测点、中测点和后测点.其中前测点位于低压压气机机匣前安装边右侧;中测点位于安装在扩散机匣上的点火燃油喷嘴支架上部;后测点通过低压涡轮轴承座振动传感器组件安装在 7号轴承支座的下部[7].以相对于高压转子转速的整周期进行采样,每周期采集 128个点,连续采集 16个周期.图 3为某次台架测试发生故障时,前测点所得信号的时域波形.
分析图 3可知,原始信号明显受到了噪声污染.为消除噪声对盲源分离的影响,利用开—闭和闭—开组合形态滤波器对原始信号进行滤波.图4为滤波后前测点的时域波形.
对比图 3和图 4可知,数学形态滤波器不但能够很好地滤除掉信号中的噪声,而且能够较好地保留原始信号的基本形状.中、后测点信号的滤波效果也与此类似.图 5、图 6分别为滤波处理后前、中测点振动信号的高压阶次谱,后测点振动信号的高压阶次谱如图 1所示.

图3 前测点时域波形

图4 数学形态滤波后前测点时域波形

图5 前测点高压阶次谱

图6 中测点高压阶次谱
分析图 5、图 6和图 1可知,在已知高、低压转速的情况下,高、低压转子 1倍工频及其高倍频分量可较好地区分开来,但对于次谐波即低倍频分量却无法确定是由高压转子引起还是由低压转子引起,从而无法准确定位故障原因.利用 Fast ICA分离算法对前、中、后 3个测点的信号进行独立分量分解(3个观测信号,两个独立源,满足N≥M的条件),图 7~图 10为分解所得高、低压转子的时域波形和阶次谱图.

图7 独立分量分解所得低压转子时域波形

图8 独立分量分解所得低压转子阶次谱

图9 独立分量分解所得高压转子时域波形

图10 独立分量分解所得高压转子阶次谱
对比图 7和图 9可知,Fast ICA算法分离出的高、低压转子信号明显削弱了彼此间的混叠.同时,由图 8和图 10的低、高压阶次谱图可知原高压阶次谱的 0.3倍左右次谐波分量实为低压转子的 0.5倍附近次谐波分量.因此,可进一步定位故障主要由低压转子引起.虽然盲源分离技术可以进一步提高故障定位的准确性,但分离后的信号与源信号却存在幅值和顺序上的不确定性,尽管如此,源信号的波形,即频域信息却能够较好地恢复.因此,这些不确定性并不影响故障原因的定位,某种程度上可以接受.
4 结 论
针对双转子航空发动机机匣拾取振动信号的特征,基于提高航空发动机振动状态监测和故障诊断准确性的目的,采用基于数学形态滤波前处理的盲源分离识别框架,对实测发动机振动数据的分析表明:
1)开—闭和闭—开组合数学形态滤波器不仅能够很好地滤除掉原始信号中的噪声分量,而且能够较好保留原信号的基本形状;
2)盲源分离技术虽然存在幅值和顺序上的不确定性,但分离出的信号能够显著削弱彼此间的混叠,源信号的波形得到了较好的恢复,因此能够进一步提高故障定位的精度.
References)
[1]Shi D F,Qu L D,Gindy N N.General interpolated fast fourier transform:a new tool for diagnosing large rotatingmachinery[J].Journal of Vibration and Acoustics,2005,127(4):351-361
[2]胡爱军,唐贵基,安连锁.基于数学形态学的旋转机械振动信号降噪方法[J].机械工程学报,2006,42(4):127-130 Hu Aijun,Tang Guiji,An Liansuo.De-noising technique for vibration signals of rotatingmachinery based on mathematicalmorphology filter[J].Chinese Journal of Mechanical Engineering,2006,42(4):127-130(in Chinese)
[3]郭景峰,申光宪,郑绳楦,等.数学形态学在数字滤波中的应用研究[J].机械工程学报,2002,38(10):144-147 Guo Jingfeng,Shen Guangxian,Zhen Shengxuan,et al.Application of mathematical morphology in digital filter[J].Chinese Journal of Mechanical Engineering,2002,38(10):144-147(in Chinese)
[4]张发启.盲信号处理及应用[M].西安:西安电子科技大学出版社,2006 Zhang Faqi.Operation and application of blind signal[M].Xi'an:Xi'an Electronical Science and Technology University Publishing Company,2006(in Chinese)
[5]Hyvärinen A.Fast and robust fixed-point algorithm for independent component analysis[J].IEEE Transactions on Neural Networks,1999,10(3):626-634
[6]Hyvärinen A,O ja E.A fast fixed-point algorithm for independent component analysis[J].Neural Computation,1997,9(7):1483-1492
[7]秦海勤,徐可君,江龙平.某型航空发动机机载振动监测点选择[J].推进技术,2007,28(6):697-702 Qin Haiqin,Xu Kejun,Jiang Longping.Research on distribution of airborne vibration monitoring measuring points for the aeroengine[J].Journal of Propulsion Technology,2007,28(6):697-702(in Chinese)
(编 辑 :张 嵘)
Analysis ofaero engine vibration signalbased on blind source separation technology
Qin Haiqin Xu Kejun
(Department of Aviation Mechanism,Qingdao Branch of Naval Aviation Engineering Institute,Qingdao 266041,China)
Ou Jianping
(Aerotechnics Ensure Branch of Navy Equipment Department,Beijing 100071,China)
In order to imp rove the accuracy of vibration monitoring and fault diagnosis,a blind source separation frame which is combining mathematical morphology preprocessing and Fast ICA arithmetic was brought out based on the characteristics of dual rotors aero engine case vibration signal.It is that the original signal was preprocessed by open—close and close— open combinatorialma the matical morphology.The signal noise can be well filtered,but its fundamental form can be reserved.The Fast ICA arithmetic was used to get back the high and low rotor's vibration waveform.The frame was used to analyse the real testing data.The result shows that the method can well respectively resume the high and low rotor signal frequency domain structure information.It is very helpful to improve the accuracy of fault location.
aero engine;dual rotors;blind source separation;fault location;vibration signal analysis
TH 17;TH 133
A
1001-5965(2010)11-1307-04
2009-10-09
秦海勤(1981-),男,山西临县人,博士生,q-h-q124@tom.com.
