某方钢管混凝土柱钢梁节点非线性有限元分析

凡 红 邹万山

(1.深圳市中广核工程设计有限公司,深圳 518057;2.深圳市深圳金光华实业集团有限公司,深圳 518048)

钢管混凝土结构具有承载力高、施工方便、耐火性能好、耐腐蚀性强、节点连接简单、传力可靠、经济性好等特点,从而成为当前研究的热点[1].随着钢管混凝土结构的广泛应用,节点设计问题也越来越受到关注[2].国内外学者对钢管混凝土节点也进行了大量研究工作[3-6],内隔板贯穿式钢管混凝土柱-钢梁节点是《矩形钢管混凝土结构技术规程》(CECS 159: 2004)推荐的节点形式,对这类节点的研究成果尚不多见,且规程中对其受力机理及承载力计算方法均未提及.

文献[7]进行4个节点试件的静力破坏试验研究,验证了该种节点形式的可行性和优越性,但在试验过程中,由于试验测量条件的局限性,仅通过应变片来测量关心点的应变,不便于了解整个构件的应力分布规律.本文在试验的基础上,利用ABAQUS软件建立三维有限元静力分析模型,为进一步了解内隔板外伸式钢管混凝土柱-钢梁节点提供参考.经过试验结果验证的有限元模型可以有效地弥补试验的不足之处,可以方便地了解任意一点的应变和任意时刻构件总体的应力应变分布情况,能够很好地获取试验中无法测量得到的结果,并且可以较清晰地看到各个节点试件主应力分布,以及核心混凝土的受力状态,从而获得对钢管混凝土结构的受力性能更准确、更全面的认识.

1 试件概况

试件为平面中柱节点,其中试件SZ61为规程中推荐的节点形式.试件的框架梁为组合工字形钢梁,框架柱采用冷弯空心方形钢管,钢管柱内填C40混凝土,试验钢材为Q235B.试件示意图如图1所示,试件的具体构造形式为:钢管柱在节点处断开,钢梁翼缘与外伸隔板焊接,腹板与钢管柱通过节点板用高强螺栓连接.隔板与钢梁翼缘和钢管柱的所有焊缝均采用全穿透焊接,节点板与柱壁采用双面角焊缝焊接[8].节点试件的具体截面尺寸和编号见表1,主要材性指标见表2.

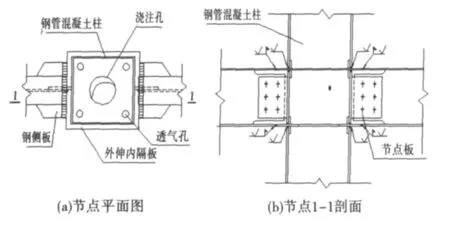
图1 节点示意图

表1 节点试件截面尺寸及编号

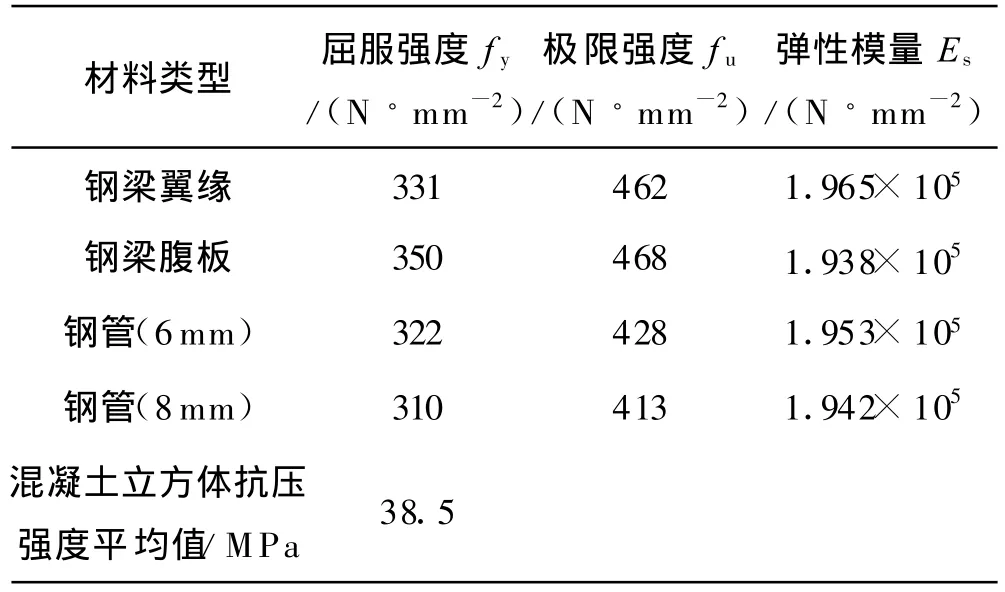
表2 材料性能参数

2 有限元模型的建立

2.1 单元类型

在本文的有限元模拟中对于钢材和核心混凝土采用八节点减缩积分格式的三维实体单元(C3D8R),虽然这种单元与其它高次等参单元相比,计算精度稍低,但却可以大大节省计算时间,从计算的经济性出发,整个模型采用C3D8R单元.

2.2 材料本构模型

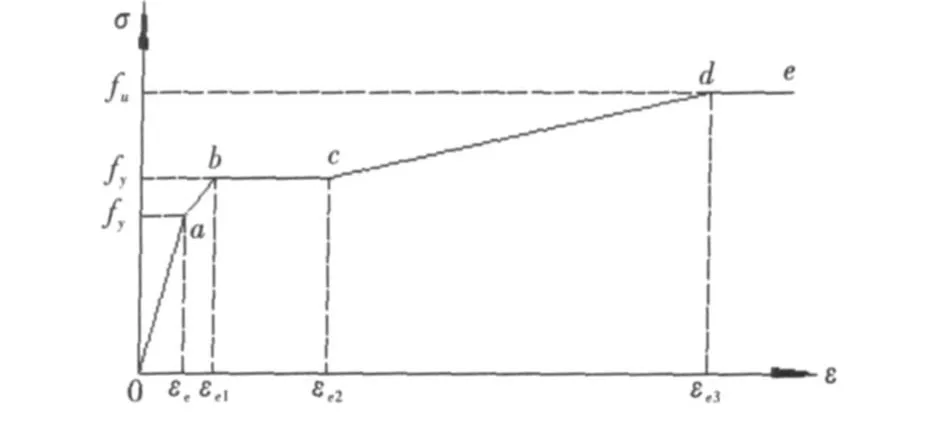
图2 钢材应力-应变曲线

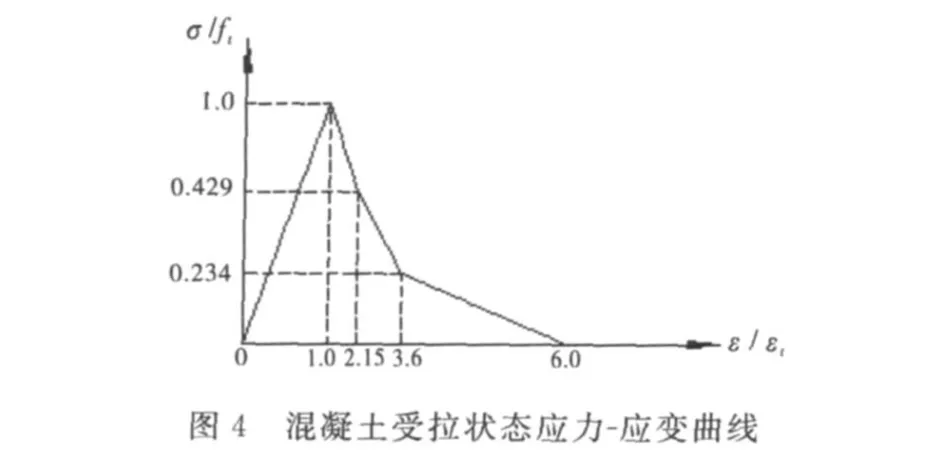
混凝土是一种脆性材料,在拉,压方向上具有不同的力学性质,各国学者对混凝土的本构提出了不同的模式.文中采用ABAQUS中的塑性损伤模型,由于混凝土材料的复杂性,其本构关系也因为受力状态的不同而不同,核心混凝土处于方钢管的围压作用下,因此受压曲线采用韩林海提出的约束混凝土本构模型,而受拉曲线则采用单轴作用下受拉本构模型[10].

2.3 模型的建立与求解

为减少单元数量,利用对称性取一半模型计算,试件的有限元整体模型如图5所示.建模时,根据受力简图,在柱端放置刚度很大的垫块,通过在垫块上施加均布面荷载来实现轴心受压.根据力学计算简图,在柱顶和柱脚设为铰节点,因此在柱顶施加x,y方向的约束,在柱脚施加 x,y,z 3个方向的约束,在对称面施加y,z平面的对称边界,求解时,首先在柱顶施加均布荷载,然后保持柱顶的荷载不变,在梁端进行位移加载.利用增量迭代法进行非线性方程组求解,采用牛顿法进行迭代计算,分析过程中考虑了几何非线性作用[11].

图5 节点三维有限元模型

3 有限元计算及结果分析

3.1 极限承载力的对比

有限元计算得到的荷载值与试验中试件的承载力对比见表3,有限元分析得到的极限荷载值和试验的破坏荷载相差较小,表明有限元模型可以较好地反映节点的实际工作状态.

表3 节点承载力试验值与有限元值对比

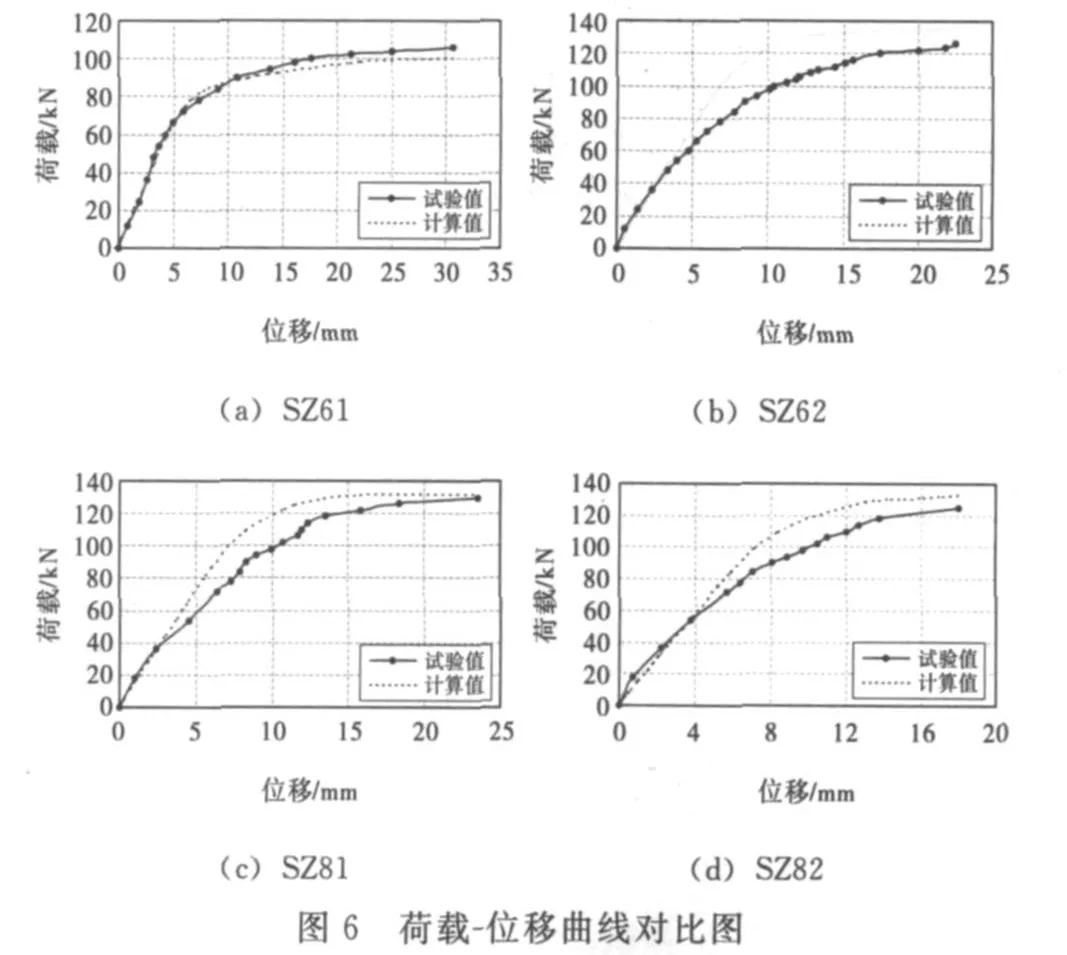
3.2 荷载-位移曲线的对比分析

从图6可以看出,试件在加载初始阶段试验值与计算值两者吻合地较好,进入非线性阶段后,后3个试件两者相差较大,试验曲线刚度比有限元模拟的刚度小,而试件SZ61两者吻合地较好.这是由于后3个试件的梁端翼缘增加了钢侧板,使梁端翼缘的宽厚比增加,钢梁的局部稳定性减小,且试件加工过程中不可避免地存在一定的缺陷,加载过程中钢梁更易发生平面外扭曲,而在有限元模拟中无法考虑构件的原始缺陷,并且对于边界条件的模拟也有一定的差异,一般情况下试验中的支座和各种支承不可能达到理论分析的绝对刚性,从而使后3个试件的荷载-位移曲线相差较大.但随着荷载的增加,变形的发展趋势一致,表明有限元方法还是能够很好地模拟构件的整体受力性能,这为进一步运用有限元方法探讨节点的受力性能提供了正确的依据.

3.3 节点内力分布及破坏机理分析

由表4中的梁柱截面抗弯刚度比η值可知,4个节点试件的方钢管混凝土柱的刚度远大于钢梁,属于典型的“强柱弱梁”,故在外荷载下,显然柱子的承载能力较梁要大得多,正如试验中节点的破坏形式,当梁端达到屈服,直到形成塑性铰或局部屈曲时,柱子及节点域仍处于弹性阶段,节点的最终破坏均为梁端破坏.从图7中可以明显看出,钢梁已经达到屈服,柱子和节点域仍处于弹性状态.

表4 节点试件的梁柱截面弯曲刚度比值

图7 SZ61节点σx应力分布云图

图8 试验中节点的破坏形式

3.4 节点的应力分析

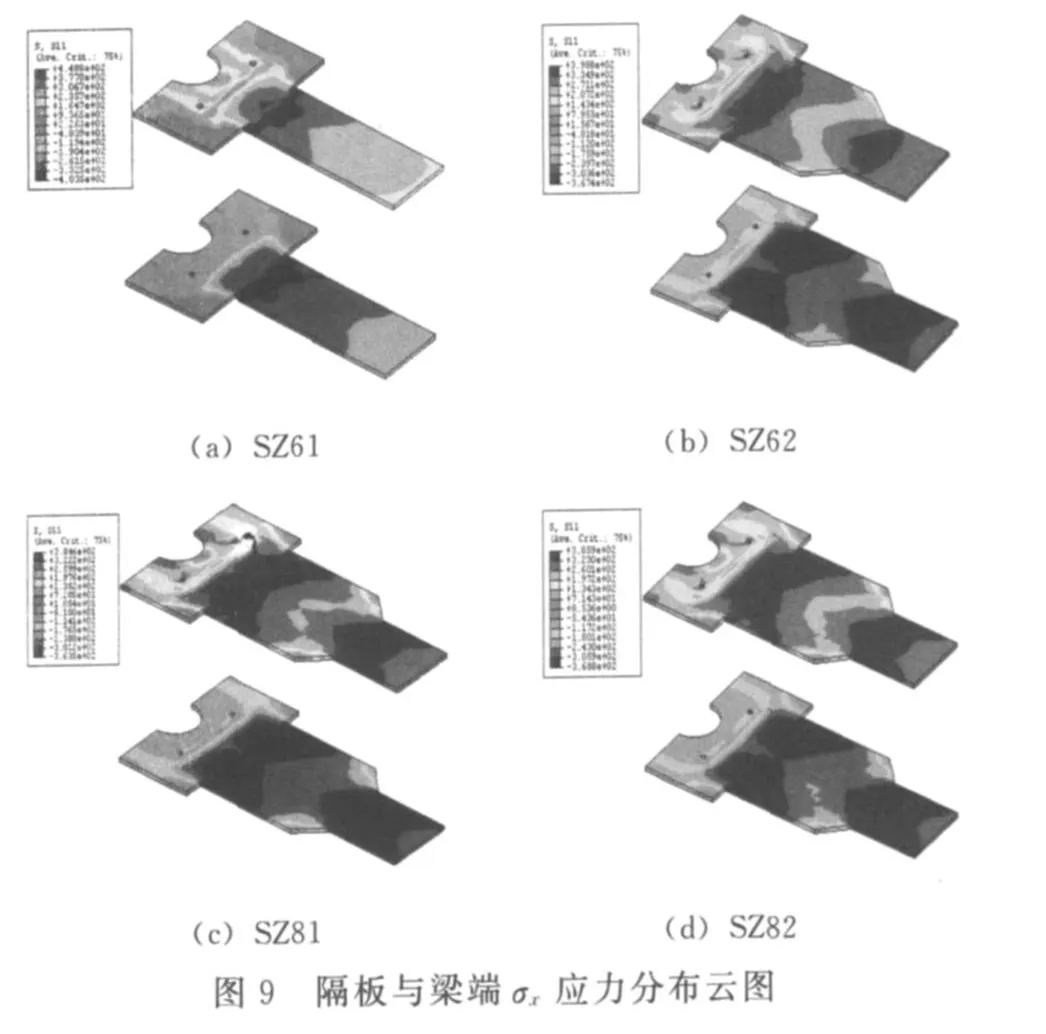
3.4.1 节点钢梁的应力分布云图

从图9中可以看出,试件SZ62梁端的拉应力比SZ61要小,SZ61隔板与梁端的应力相差较大,而后3个试件隔板与梁端的应力相差较小,表明在梁端增加钢侧板后,使梁端的应力比较均匀地传递给隔板,减缓了应力集中现象.对于后3个试件,受压翼缘的应力比较接近,而受拉翼缘的应力分布SZ81和SZ82的应力分布比较接近,SZ62的拉应力稍大于SZ81,表明隔板的外伸长度和柱的宽厚比对钢梁翼缘的受力影响较小.

3.4.2 节点隔板的应力分布云图

从隔板的应力分布云图图10可以看出:(1)4个节点试件的上隔板应力分布比较均匀,而下隔板在与混凝土交界处Mises应力减小很多,这表明节点上隔板承担了上翼缘传来的拉应力,而压应力则通过下隔板传递给了核心混凝土柱,从而使下隔板的Mises应力分布较上隔板要小.(2)比较试件SZ61和SZ62的应力云图可以发现,在梁端增加钢侧板后,隔板的有效净截面与钢梁梁端的截面相差较小,隔板的应力分布比较均匀.而试件SZ61应力分布在中间趋于均匀,角部的应力很小.(3)试件SZ81和SZ82的应力云图分布比较相似,试件SZ62上隔板的应力稍小于SZ81上隔板的应力,而下隔板的应力则稍大于SZ81下隔板的应力,表明隔板外伸长度的改变对节点受力影响较小,而宽厚比对隔板的受力有一定的影响.

综上所述,隔板的应力云图的显示规律与试验中应变片测得的应变变化规律是一致的.上隔板主要承担翼缘传来的拉力,而下翼缘传过来的压应力则通过隔板传递给了核心混凝土.

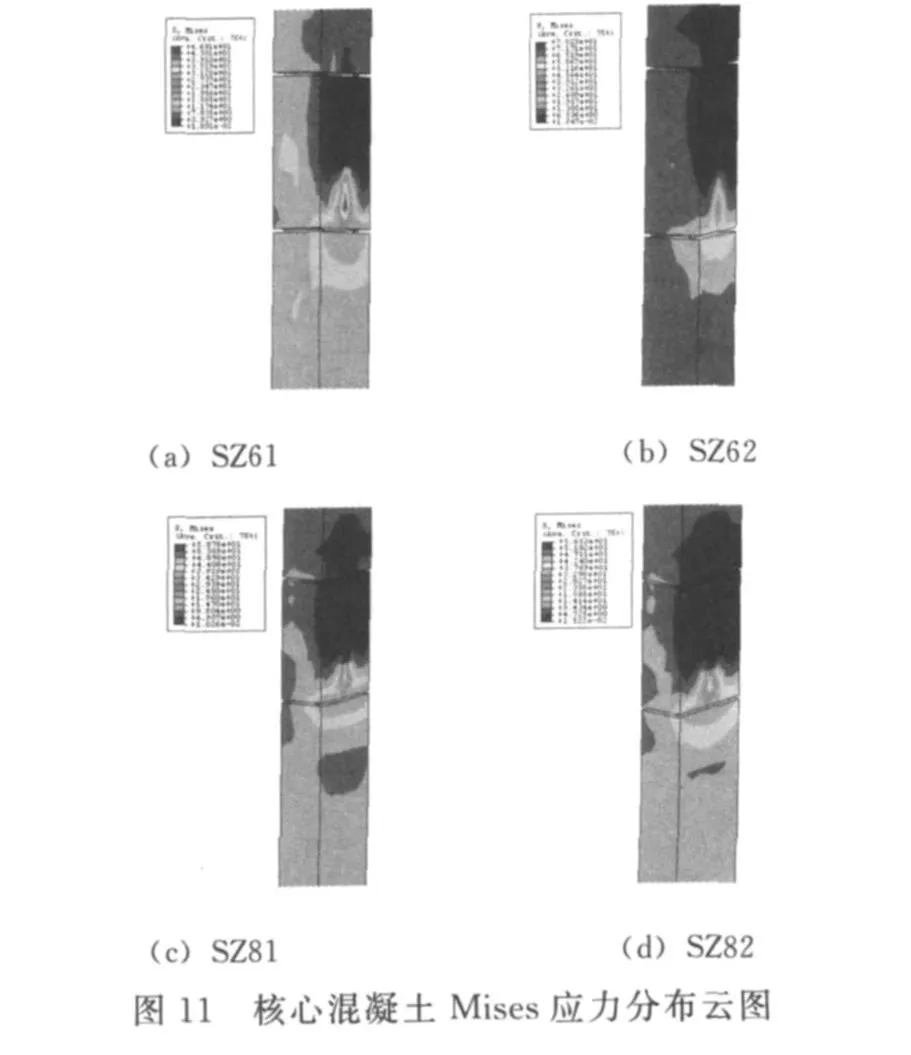
3.4.3 核心混凝土

核心混凝土柱下隔板处的Mises应力比较大,而上隔板处的应力比较小,表明在上隔板处主要由隔板来承受拉力,核心混凝土并未承受很大的力,而在下隔板处,则节点的压应力由隔板传递给了核心混凝土柱来承担.

4 结 论

本章通过对节点建立有限元模型,对试件进行了三维非线性有限元分析,通过对计算结果的分析,可以得到以下结论:

(1)有限元分析得到的梁端荷载-位移曲线与试验得到的荷载-位移曲线吻合较好,由于理论分析较试验的边界条件,材料性质等因素要理想一些,且理论模型与试验模型之间总存在着一定的差距,使得试验的曲线刚度比理论计算的小.

(2)有限元分析结果表明内隔板外伸式钢管混凝土柱-钢梁节点的传力路径清晰明确,柱的刚度远大于钢梁的刚度,满足“强节点,弱构件”的抗震设计原则.

(3)有限元分析与试验观察到的试件破坏过程,应力及变形规律一致,表明所建立的三维有限元模型是合理的,进一步明确了该类节点的力学性能和工作机理.

[1] 钟善桐.钢管混凝土结构[M].3版.北京:清华大学出版社,2003.

[2] 韩林海,杨有福.现代钢管混凝土结构技术[M].北京:中国建筑工业出版社,2004.

[3] 王毅红,郭增辉,李先顺等.带有芯钢管的钢管混凝土节点的受力机理[J].建筑工程与科学学报,2007,24(1): 64-68.

[4] 聂建国,秦 凯,张桂标.方钢管混凝土柱内隔板式节点的抗弯承载力研究[J].建筑工程与科学学报,2005,22 (1):42-49.

[5] Hu H T,Huang C S,Wu M H,et al.Nonlinear Analysis of Axially Loaded Concrete-filled Tube Columns with Confinement Effect[J].Journal of Structural Engineering,2003,129(10):1322-1329.

[6] Hu H T,Huang C S,Chen Z L.Finite Element Analysis of CFT Columns Subjected to an Axial Compressive Force and Bending Moment in Combination[J].Journal of Constructional Steel Research,2005,61(12):1692-1712.

[7] 凡 红,徐礼华,杜国锋.方钢管混凝土柱-钢梁节点静力性能试验研究[J].湖南大学学报:自然科学版,2007.

[8] 矩形钢管混凝土结构技术规程(CECS 159:2004).北京:中国计划出版社,2004.

[9] 韩林海.钢管混凝土结构-理论与实践[M].北京:科学出版社,2004.

[10]Cozzarelli F A,Bernasconi G.Non-linear Creep Damage Under One-dimensional Variable Tensile Stress[J].International Journal of Non-liear Mechanics,1981,16 (1):27-38.

[11] Hibbitt,Karlson,Sorenson.ABAQUS Version 6.4: Theory Manual,Users'Manual,Verification Manual and Example problems M anual[M].Hibbitt,Karlson and Sorenson Inc.,2003.