地震对软弱夹层边坡稳定性影响数值模拟研究

杜晓丽 宋宏伟 魏京胜

(1.中国矿业大学建筑工程学院,江苏徐州 221008;2.深部岩土力学与地下工程国家重点实验室,江苏徐州 221008)

由于软弱夹层诱发的岩质边坡失稳事故占有十分重要的地位[1-4],国内学者对软弱夹层对边坡稳定性的影响进行了大量研究,并取得了许多有意义的成果.文献[5-7]利用相似实验模型,从不同的角度分析了地震加速度、结构面走向对边坡稳定性的影响,并总结边坡失稳破坏的模式;文献[8-10]利用数值模拟法研究动荷载作用规律,得到许多有意义的结论.基于地震波通过结构面时的传播理论,文献[11-12]给出了有摩擦滑移情况下爆炸应力波通过软弱结构面时的时反射关系,并讨论了结构面上的摩擦滑移条件和能量损耗问题;文献[13-14]建立了软弱夹层的透射模型,并对薄软弱夹层的隔振性能进行了研究;文献[15]归纳了二维波穿过非连续结构面后的透射率特性,对其隐含意义进行了深入研究.然而,至今有关软弱夹层岩质边坡研究还不够深入.

借助ADINA数值模拟软件对有无软弱夹层的岩质边坡稳定性进行数值分析,强调均质岩质边坡与含软弱夹层岩质边坡在破坏位置和破坏程度方面的差异;研究结构面倾角、厚度与质点位移、速度的关系,进而探讨结构面倾角对边坡稳定性的影响.

1 数值模型的建模和求解

1.1 数值模型

考虑软弱夹层的位置,确定边坡模型边界范围为:沿水平Y方向取150 m,沿垂直Z方向取150 m.考虑到平面应变问题,沿垂直于YZ平面方向取60 m,建立三维数值模型.模型中软弱夹层的厚度分别为5m、10m、15m,倾角分别为15°、30°、45°、60°、75°、90°、120°、150°,如图1所示,所需力学参数见表1.其中,图1为夹层厚度10m,坡角60°的边坡数值模型.为了对比需要,添加了一个去掉软弱夹层均质模型.

图1 计算模型示意图

表1 岩体力学参数

1.2 模型边界和求解

(1)边界条件:在模型底边界上设置全固定位移约束;在左右两侧设置垂直于边界的位移约束;坡面无约束.

(2)施加荷载:在不考虑构造应力的情况下,施加沿水平负方向的EL-Centro波[16]地震荷载,如图2所示;并假定地震持时20s.

(3)岩体材料:均选用莫尔库仑材料.

(4)网格划分:网格划分时定义单元线段的长度为5m,并采用8节点六面体三维空间单元划分网格.

(5)求解:采用动力时程分析法求解运动平衡方程.

图2 地震波加速度时程曲线

2 影响因素分析

2.1 软弱夹层对岩质边坡稳定性的影响

边坡水平方向位移分析.由图3～4位移等值线图可知,均质岩质边坡的位移变化显著部位主要分布在坡腰、坡顶两处;而含软弱夹层的岩质边坡位移变化主要分布在软弱夹层到坡面的部分岩体中.均质边坡(见图3)中,坡腰部位的质点位移大多为负值(文中规定:质点运动方向与坐标轴的正方向一致时,质点参数为正;反之为负,下文亦同),最大值约为-3.3 mm,且位移变化随坡内岩体与坡面距离的增加而逐渐减小;坡顶部位的质点位移全部为正值,最大值(2.7mm)要比坡腰处的小.含软弱夹层的岩质边坡(见图4),位移变化集中在从坡面到软弱夹层的上部岩体中,且位移量从坡面上的最大值12.1 mm逐渐减小到软弱夹层带中的5.0 mm左右.而在坡脚及远离软弱夹层部位的位移变化甚微,与均质边坡的位移变化走势相似.

边坡水平方向变形分析.通过图5可见,仅在靠近坡顶与边坡后壁之交的部位应变区域比较明显,而坡面及坡体内部的应变则非常小.分析得边坡后部出现较大应变的原因存在两种可能:一是边坡后壁垂直,属于陡峭边坡;二是地震荷载经过边坡后壁时,因其后没有传播介质,岩体因受到反射拉伸波的作用而可能导致崩塌破坏.图6为边坡内含有软弱夹层的应变等值线图,其变形主要集中在坡面附近的软弱夹层带内,且应变从坡面处的最大值1.976×10-3急剧减小到软弱夹层带边缘的-1.606×10-4;而远离软弱夹层部位的岩体变形甚微,几乎不受地震荷载的影响.

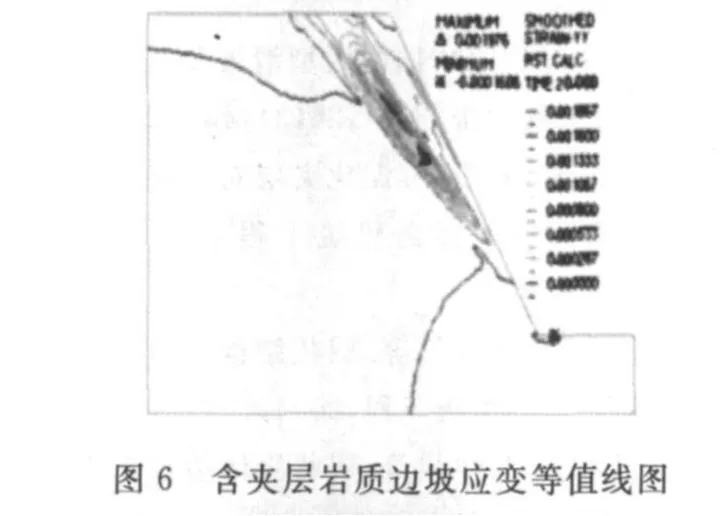
由上述分析可知:地震荷载作用下,均质边坡与含软弱夹层的岩质边坡变形部位与破坏程度有显著差异.就变形破坏的部位而言,均质边坡的变形部位主要在坡顶或坡面附近;而含软弱夹层边坡的变形部位与软弱夹层的空间展布有关,破坏部位主要集中于软弱夹层分布带内.就破坏程度而言,含软弱夹层岩质边坡发生破坏的概率远比均质边坡的高,且岩体内质点最大位移值前者是后者的3.6倍;最大应变前者约为后者的10倍.

2.2 水平位移和结构面倾角对边坡稳定性的影响

依据有限元计算的收敛性[18-19]、表2(表中数据为地震荷载作用下通过数值模拟获得地最大计算时步)及图7可知,当夹层厚度为5m时,不论结构面倾角为多大,边坡一直处于稳定状态.而夹层厚度为10 m、15 m时,结构面倾角β≤45°时,边坡已失稳破坏;结构面倾角β≥60°时,边坡尚处于稳定状态.

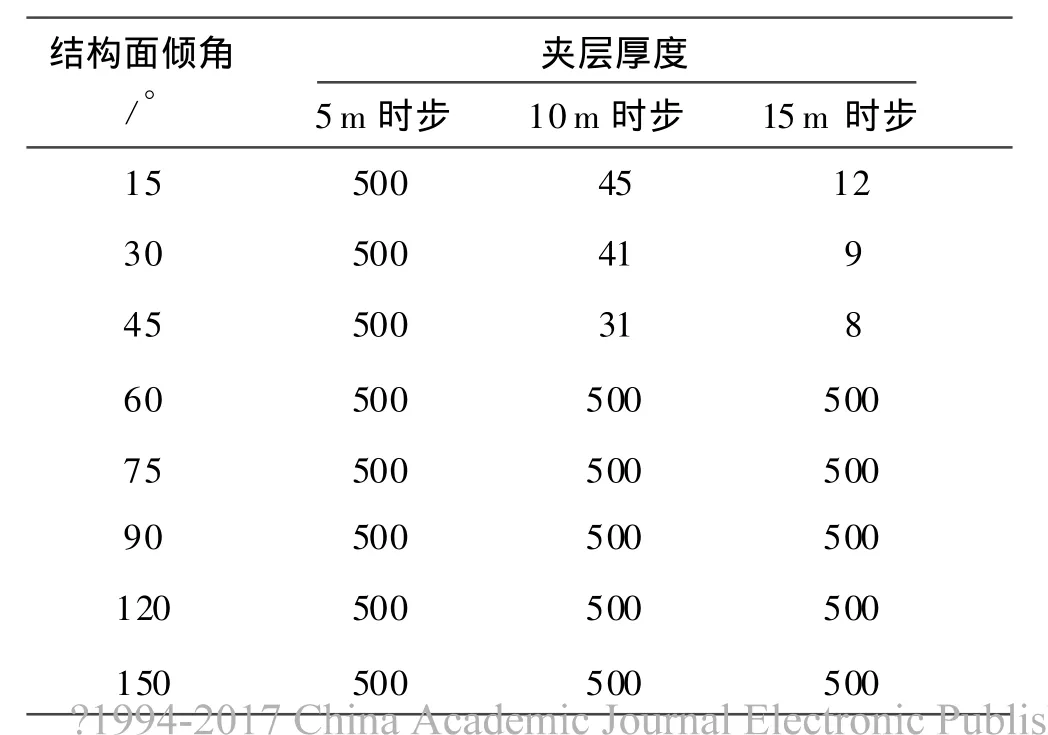
表2 各类边坡的计算时步

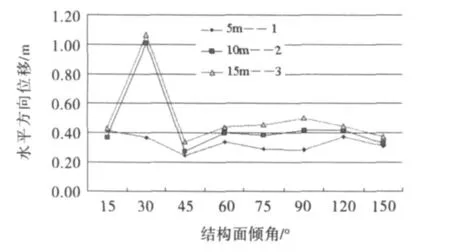
图7 位移与结构面倾角的关系

由图7还知,边坡水平位移并不随着结构面倾角的变化而单调递增或递减,而是随着结构面倾角的变化而变化.即当15°≤β≤45°时,随着β的逐渐增大,边坡水平位移逐渐减小,意味着边坡抵抗地震荷载的破坏能力随着结构面倾角增大而降低;而当45°＜β＜60°时,边坡水平位移反而开始增大,表明边坡抵抗破坏能力随着结构面倾角的增大而增大;当60°＜β＜180°时,边坡水平位移随着结构面的倾角的变化走势基本一致,但由于反倾的软弱夹层在坡面上出露,其抗剪能力相对较低,易导致边坡发生局部失稳破坏,致使结构面倾角在120°左右时水平位移变化显著.

2.3 水平速度和结构面倾角对边坡稳定性的影响

由图8可知,折线1、2、3中的质点速度随着结构面倾角的变化走势基本一致,且夹层越厚水平方向的速度就越大.但软弱夹层倾角在15°～45°之间时,折线2、3中速率变化急剧,而折线1则比较平缓.存有这种差异的原因在于:折线2、3的边坡在软弱夹层倾角为30°时已经失稳破坏,而折线1中边坡处于稳定状态.

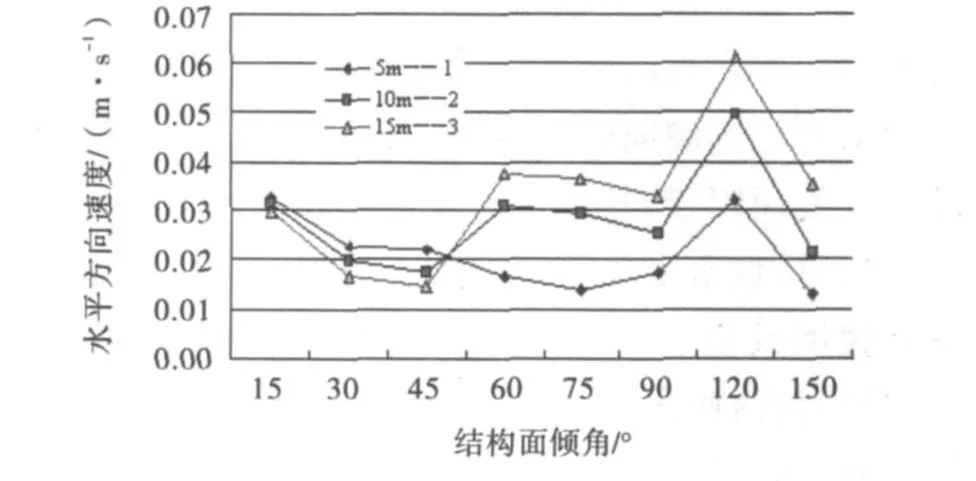
图8 速度与结构面倾角的关系

3 边坡稳定性判据的讨论

依据有限元计算的收敛性,由表2可知:结构面倾角β≤45°时,厚度分别为10 m、15 m的软弱夹层边坡已破坏,而β≥60°的各类边坡均处于稳定状态.显然,在45°＜β＜60°之间,必定存在一个的特定角度,这个角度就是边坡从失稳破坏状态到稳定状态的转折点,即为边坡处于极限平衡状态时的临界角.再由图7可知边坡稳定性与结构面倾角的关系:结构面倾角15°≤β≤60°时,边坡的稳定性均随着结构面倾角的增大先减小后增大;而且边坡失稳破坏时的最大位移与稳定状态时的最小位移存在显著差异,如曲线3中边坡失稳破坏时质点的最大位移为15 mm(β= 45°),而边坡处于稳定状态时质点的最小位移为38 mm(β=60°),显然存在质点位移突变现象.

由以上可认为:边坡的稳定性与结构面倾角存在直接关系,在结构面倾角约为50°时,存在一个临界角使得边坡处于极限平衡状态.而结构面倾角小于临界角时边坡将失稳破坏;结构面倾角大于临界角时,尽管在地震荷载的作用下边坡的稳定性将降低,但边坡仍能处于稳定状态.由于结构面倾角在工程实践中便于获得,且结构面倾角的大小与边坡的稳定性密切相关,故本文建议采用结构面倾角作为岩质边坡稳定性的判据.

由于本文选用的数值模型尚不够充分,未得到逼近岩体极限平衡状态时的临界角.欲获得这个特定的角度,还需要对结构倾角45°＜β＜60°的软弱夹层岩质边坡进行深入研究.

4 结 论

通过对有无软弱夹层,不同厚度、倾角的软弱夹层岩质边坡进行数值模拟分析及讨论,得到以下结论:

(1)地震荷载作用下,含软弱夹层岩质边坡与均质岩质边坡变形部位和破坏程度有显著差异.软弱夹层边坡的变形与内含夹层的空间展布有关,主要集中在软弱夹层到坡面间;而均质边坡的变形主要集中在坡顶或坡面附近;且前者的破坏程度远大于后者.

(2)边坡水平位移并不随着结构面倾角的变化而单调递增或递减,而是随着结构面倾角的变化而变化.当结构面倾角一定时,质点振速受软弱夹层厚度的影响,即夹层越厚,质点振速就越大;夹层越薄,质点振速就越小.

(3)边坡的稳定性与结构面倾角存在直接关系:即存在一个约为50°的临界角度,使得边坡处于极限平衡状态.而结构面倾角小于临界角时,边坡可能发生失稳破坏;结构面倾角大于临界角时,边坡能够抵制地震荷载的作用.

(4)研究软弱夹层岩质边坡时,建议采用结构面倾角作为边坡稳定性的判据.

[1] CHARLESJAEGER.Rock Mechanics and Engineering [M].London:Cambridge University Press,1972:340-359.

[2] 刘红星,苏爱军,王永平等.软弱夹层对斜坡稳定性的影响分析[J].武汉理工大学学报:交通科学与工程,2004, 28(5):766-770.

[3] 黄润秋.20世纪以来中国的大型滑坡及其发生机制[J].岩石力学与工程学报,2007,26(3):434-454.

[4] 王在泉,张黎明,贺俊证.泥化夹层对边坡稳定性影响及控制方法研究[J].青岛建筑工程学院学报,2004,25 (4):1-4.

[5] 门玉明,彭建兵,李寻昌等.层状结构岩质边坡动力稳定性试验研究.世界地震工程,2004,20(4):131-136.

[6] 赫建斌,门玉明,彭建兵等.层状岩体边坡动力稳定性模型试验研究[J].公路交通科技,2005,22(6):72-75.

[7] 梁庆国,韩文峰,马润勇等.强地震作用下层状岩体会破坏的物理模拟研究[J].岩土力学,2005,26(8):1307-1311.

[8] 赵 坚,陈寿根,蔡军刚等.用UDEC模拟爆炸波在节理岩体中的传播[J].中国矿业大学学报,2002,31(2):111-115.

[9] 姜 彤,马 莎,许 兵等.边坡在地震作用下的加卸载响应规律研究[J].岩石力学与工程学报,2004,23(22): 3803-3807.

[10]夏 祥,李俊如,李海波等.爆破荷载作用下岩体震动特性的数值模拟[J].岩土力学,2005,26(1):50-56.

[11]李夕兵,赖海辉,古德生.爆炸应力波斜入射岩体软弱夹层结构面的透反射关系和滑移准则[J].中国有色金属学报,1992,2(1):9-14.

[12]李夕兵.论岩体软弱结构面对应力波传播的影响[J].爆炸与冲击,1993,13(4):334-342.

[13]范留明,李 宁.软弱夹层的透射模型及其隔震特性研究[J].岩石力学与工程学报,2005,24(14):2456-2462.

[14]范留明,闫 娜,李 宁.薄弹性软弱夹层的动力响应模型[J].岩石力学与工程学报,2006,25(1):88-92.

[15]雷卫东,ASHRAF,腾 军等.二维波穿过单节理的透射率特性及其隐含意义[J].中国矿业大学学报,2006,33 (1):493-497.

[16]赵大鹏.拱形断面地下结构抗震试验研究[D].南京:河海大学,2003.