QUALITATIVE ANALYSIS OF A MODIFIED HOLLING-TANNER MODEL WITH SMITH GROWTH

YANG Xiao-feng, JIN Zhen, REN Bian-qing

(Mathematics Department, North University of China, Taiyuan 030051, China)

0 Introduction

In order to precisely describe the real ecological interactions between species, Robert May developed a model, also known as the Holling-Tanner prey-predator model:

(M1)

Clearly this model incorporates intraspecific competition among the predators. The local stability of the unique positive equilibrium was investigated by May[1]and Murray[2]. Hsu and Huang[3]obtained some results on the global stability of the positive equilibrium. Peter[4]、Saez[5]and Gasull[6]studied the behavior about limit cycle and bifurcation,etc.

Recently, some researchers have made some modified or other works[7-10]. In Holling-Tanner model, it is assumed that the evolve of prey is dominated by Logistic model. Smith proposed a new model to replace the known Logistic model in 1980[11]. So it may be better fit to some reality for Smith model to replace Logistic model in Holling-Tanner model.

1 A Modified Model with Smith Growth

To fit the reality better, we can replace the logistic growth of prey population in (M1) with the Smith grow. Thus, the model (M1) is changed as follow:

(M2)

There are eight parameters in system (M2), it is bad to our analysis. So, we take nondimensional transformation to reduce the amounts of parameter at the first place.

(M3)

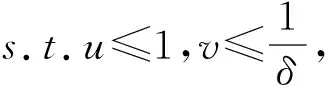
The proof is easy and we omit it.

Let the right hand of the system (M3) equal to zero, then one can obtain the equations about equilibria as following:

(1)

Setφ(u):=δ(1-u)(u+β)-u(1+αu), then due to the discriminant of equationg(u=0) is greater than 0, it has two roots, but only one of which is positive. So, think of the ecological meaning, only two of which are meaningful, the system (M3) has two equilibria:E1(1,0) andE*(u*,v*), whereu*>0 is the positive solution ofφ(u)=0.

To study the stability of these equilibria, we come to get the community matrix of system (M3), that is

2 Stability Analysis of Equilibria

(1)For the semi-trivial equilibriumE1(1,0), the community matrix of the system (M3) at it is

(2)For the non-trivial equilibriumE*(u*,v*), the community matrix of the system (M3) at it is

(2)

TodeterminethestabilityofE*,wecometocomputethedeterminationandtrailofJE*andobservetheirsigns.From(2),wecanget

(3)

Hence, the stability of the equilibriumE*are determined by the sign of

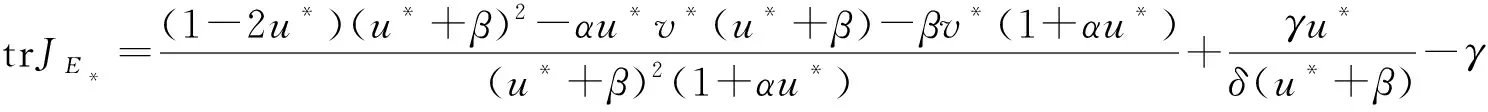
(4)

(1)CaseⅠ.IfthefollowingconditionH1issatisfied,thenf(u)>0.

(2)CaseⅡ.IfthefollowingconditionH1issatisfied,thentheequationf(u)=0hasnoroot,hencef(u)>0holdstill.

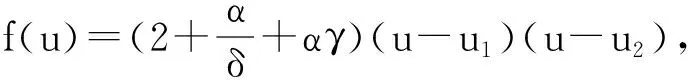
H3: 1-β-γ-αβγ>0andΔ>0.

Note1-β-γ-αβγ>0,itistruethat1-β>0 ,whichfollowsg′(u) >0.Hence,onecanfindu1u2tothecondition(c): δ>g(u2).

From(4),wecanseethesignoftrJE*is determined byf(u*), but the sign off(u*) is dominated by the conditions H1～H3 and (a)、(b) 、(c). Now, we can conclude that trJE*<0 holds true if and only if the condition H1 or H2 holds, or H3 and one of the alternative conditions (b) and (c) hold. If the condition (a) is met while the condition H3 holds ture, then trJE*hold positive, when the two equilibria are unstable and the system (M3) has at least a limit cycle by Poincare-Bendixson theorem. So we can make the following conclusion:

Theorem: The equilibriumE1is a saddle,E*always exists and

i)If 1-β-γ-αβγ≤0, thenE*is stable ;

ii)If 1-β-γ-αβγ>0 andΔ<0, thenE*is stable ;

iii)If 1-β-γ-αβγ>0 andΔ>0, thenE*is stable whenδg(u2),E*is unstable wheng(u1)<δ

3 Qualitative Behavior at the Origin (0,0)

The system (M3) is defined badly at (0,0) and consequently we redefine it as follows

(M4)

ThetrivialequilibriumE0(0,0)alwaysexistsforthemodelsystem(M4),butthesystemisnotlinearizableatE0.TodiscussthequalitativebehavioratE0,wecanperformaBriot-Bouquettransformation.

(M5)

[1] R.M.May. Stability and Complexity in Model Ecosystems[M]. Princeton University Press, Princeton, N.J., 1974.

[2] J. D. Murray. Mathematical Biology[M]. Springer-Verlag, Berlin, 1989.

[3] Sze-Bi Hsz, Tzy-Wei Huang. Global stability for a class of predator-prey systems[J].SIAM Journal on Applied Mathematics, 1998,55(3):763-783.

[4] Peter A.Braza. The bifurcation structure of the holling-tanner model for predator-prey interactions using two-timing[J]. Acta SIAM J.Appl.Math.,2003,63(3):889-904.

[5] E.Saez,E.Gonzalez-Olivares. Dynamics of a predator-prey model[J].SIAM Journal on Applied Mathematics, 1999,59(5):1 867-1 878.

[6] Armengol Gasull, Robert E. Kooij, Joan Torregrosa. Limit cycles in the Holling-Tanner model[J]. Publicacions Matematiques, 1997,41:149-167.

[7] Tapan Saha, Charugopal Chakrabarti. Dynamical analysis of a delayed ratio-dependent Holling-Tanner predator-prey model[J]. J.Math.Anal.Appl.,2009,(3):072.

[8] Mainul Haque,Ezio Venturino. The role of transmissible diseases in the Holling-Tanner predator-prey model[J]. Theoretical Population Biology, 2006,70: 273-288.

[9] Zhiqing Liang,Hongwei Pan. Qualitative analysis of a ratio-dependent Holling-Tanner model[J]. J.Math.Anal.Appl.,2007,334:954-964.

[10] Zhiqi Lu, Xia Liu. Analysis of a predator-prey model with modified Holling-Tanner functional response and time delay[J]. Nonlinear Analysis: Real World Applications, 2008,(9):641-650.

[11] F.E.Smith. Population dynamics in Daphnia magna and a new model for population growth[J]. Ecology, 1980,44:655-663.