对苏教版教材《认识分数》编排的思考

2010-02-10陈士文

教学与管理(小学版) 2010年11期

陈士文

关于分数意义的教学，苏教版教材编排在三个年级、四个单元中，分别是：三年级上册《认识分数》(3课时)、三年级下册《认识分数》(6课时)、五年级下册《认识分数》(10课时)、六年级上册《认识百分数》(9课时)。此外，关于分数内容的教学还有六个单元，分别是：《分数的基本性质》(9课时)、《分数加法和减法》(5课时)、《分数乘法》(9课时)、《分数除法》(8课时)、《分数四则混合运算》(7课时)、《百分数的应用》(1l课时)。分数内容的教学一共是十个单元，教学总量为77课时，比一学期的课时总量还多，教学时间跨度为五个学期，字数篇幅相当于一本数学教材。

对于如此的编排及教学，是不是把简单问题复杂化了?到底如何认识分数?分数的意义何在?现行苏教版教材(下面简称教材)中关于分数知识的编排是否需要进行彻底的变革呢?

一、分数与“1”的关系

认识分数是数的认识的一次扩展，对于分数的认识要从自然数的认识中“生长”出来，而不是另起炉灶。

学生第一次认识分数，教材是这样设计的(见下图)：此设计正如三年级上册教材第104页《你知道吗》栏目所述：“在古代，人们在分东西(果实、猎物等)时经常出现结果不是整数的情况。于是，渐渐产生了分数。”

“1/2”是一个最直观的分数，学生有“一半”的生活经验，“1/2”也是一个最经典、最简洁的分数，它是“1”的一半，是学生认识自然数后的一次“生长”，教材此时应比较“1/2”与“1”的大小，接着比较“1/3”、“3/2”、“1/4”、“4/5”等与“1”的大小，并引出真分数、假分数的概念，或此时借助数轴认识分数也是很好的编排设计。但教材接下来没有比较分数与自然数“1”的关系，而转向比较“1/3”与“2/3”的大小了，还有比较“3/5”与“2/5”的大小等等。教材中分数之间的大小比较固然需要，但更重要的是分数与已学自然数之间大小关系的比较，要让学生在比较中扩展数的认识。

等到学生第二次接触分数的三年级下册，教材却是这样编排的(见下图)：

把一盘桃平均分给4只小猴，每只小猴分得这盘桃的几分之几?

很显然，此时的“1/4”已不是“人们在分东西(果实、猎物等)时经常出现结果不是整数的情况”。学生很疑惑：明明是1个桃，却要用1/4来表示，是不是简单问题复杂化了呢?当然，教材的意图是扩展分数的意义，此时的1/4不是把1个桃平均分成4份中的1份，而是1个桃是4个桃的几分之几。三年级的小学生时隔半年再来接受这样的“分数意义”是否恰当?

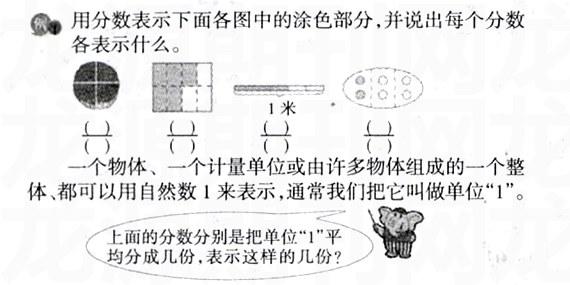
学生第三次接触“认识分数”是五年级下册，此时教材已总结出单位“1”的概念和分数的定义(见下图)。

教材通过所谓单位“1”的扩展，把分数的“量”与“率”混杂在一起。我们知道自然数“2”的意义和“2倍”的意义不是一回事，“2”是独体，是抽象出来的，“2”就是“2”，而“2倍”是表示两个量之间的关系。

面对分数的意义，我们思考：要不要建立单位“1”的概念?分数的认识是不是先从“量”的角度开始?分数的大小始终和“1”等自然数在一起比较，是不是更明晰，更利于小学生接受?是不是在教材编排时先解决好分数的由来，分数的读写，分数的分类，分数与自然数的大小关系会更好?

二、分数的“量”与“率”

分数的意义，即分数“量”的意义和“率”的意义。当学生建立了分数“量”的意义后，教材编排可借助自然数“倍”的意义引申扩展出分数的意义。譬如：

这样编排学生对分数意义的认识有一种自然迁移的便捷，又是在一个更大的整体中建构分数的意义，并且和将来学习百分数的意义统一起来。而教材中分数的“量”和“率”混杂一处，以至于五年级下册教材出现了这样的习题：

说出每个分数表示的意义。

(3)一节课的时间是2/3小时。

请问：“一节课的时间是2/3小时”中的“2/3”的意义怎么说呢?是认识“量”还是“率”?

本来“1”就是“1”，哪来的单位“1”，教材不必生造出单位“1”的概念来。综上思考，分数的认识分两个阶段进行，第一阶段，认识分数如同认识自然数一样，可在数轴上呈现。第二阶段，认识分数借助“倍”的意义，认识到分数可表示一个量是另一个量的几分之几。这样编排，一是便于小学生逐步建立分数的概念，二是体现数学的系统性、和谐性，三是减少分数教学课时量，以便于用于其他内容的教学。

三、分数与除法的关系

分数就是因“除”而“生”的，教材在三年级上册《认识分数》时完全可以呈现下面的算式：

4÷2=22÷2=11÷2=1/2

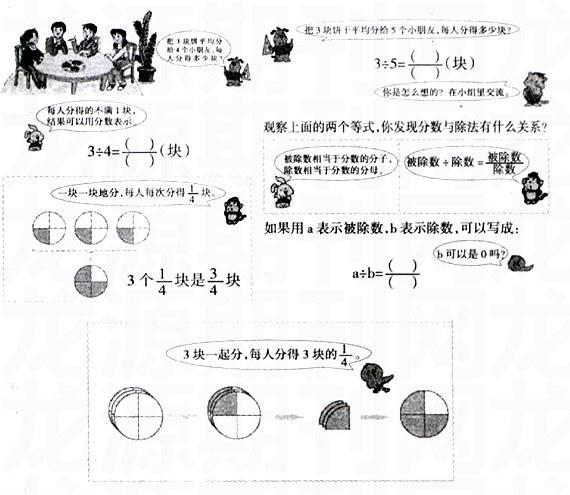
一开始认识分数就很自然地让学生明白分数与除法的关系，而不是费尽周折直至五年级下册教材还这样编排(见下图)：