空间矢量PWM多相变频调速系统非正弦供电技术

刘东， 黄进， 于文娟， 康敏， 杨家强

（1．浙江大学电气工程学院，浙江杭州 310027;2．浙江科技学院 自动化与电气学院，浙江 杭州 310023）

0 引言

多相电动机通过增加电机相数来实现低压大功率，电机相数的增多，使得影响较大的空间谐波次数增大，且幅值下降，转矩脉动下降。转子电流接近正弦，转子损耗下降，可靠性提高。多相电机在定子缺相时仍可以降功率启动和运行，适合高可靠性要求的领域。多相电机由多相逆变器来驱动，二者与控制器一起构成完整的多相变频调速系统［1－2］。

H．A．Toliyat等人［3］对五相变频调速系统进行了大量的研究，提出了五相逆变器的空间电压矢量脉冲宽度调制（PWM）的控制方法，但这种方法只是三相系统SVPWM控制方法的简单扩展。G．Grandi和 Hung-Min Ryu 等人［4－5］提出了基于多 d-q 平面的空间电压矢量SVPWM，但只是分析了输出正弦电压SVPWM（SSVPWM）和只采用最大空间电压矢量调制等几种特殊情况，并没有分析各d-q平面参考电压矢量如何确定的情况。

H．A．Toliyat等人［6－7］还从电机设计的角度分析认为，电机具有集中整距绕组，逆变器输出方波电压（电流），此时整个系统的性能最佳。保持齿部磁密幅值和定子铜耗分别相等，在电流源供电的一台五相集中整距绕组感应电机中注入15%的三次谐波电流。实验结果表明，电机性能有所改善。然而H．A．Toliyat等人的研究中只是保持齿部磁密幅值和定子铜耗分别相等，此时轭部磁密变成尖顶波，轭部存在局部饱和，对电机性能不利。随着相数增大，自由度增加，可利用的谐波更多，有利于改善磁密波形，可同时保持齿、轭部磁密幅值分别相等、定子铜耗相同，电机性能随着相数增加而改善。

本文建立了输出非正弦电压SVPWM（NSVPWM）的数学模型，分析了 NSVPWM与谐波注入PWM的内在联系，并给出了NSVPWM中各d-q平面参考电压矢量的给定方式。以九相集中整距绕组感应电机为例，在保持齿、轭部磁密幅值分别相等、定子铜耗相同的前提下，对其分别在SPWM、SSVPWM和NSVPWM控制策略下的输出转矩进行比较。

1 九相电压源逆变器空间电压矢量分析

九相电压源逆变器的拓扑结构如图1所示，负载星型连接，一个隔离中点。设九相电压源逆变器的开关变量为 S1，S2，S3，S4，S5，S6，S7，S8，S9。Sk表示第k个逆变器桥臂的开关状态，若Sk=1，表示逆变器第k个桥臂上开关导通，下开关关断;若Sk=0，则反之。逆变器第k个桥臂的输出电压可表示为Vk=SkVdc，Vdc为直流母线电压，因此九相逆变器输出相电压可表示为［8］

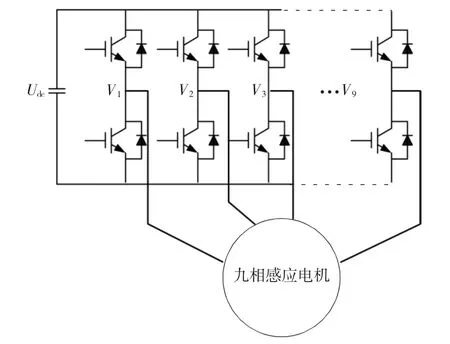
图1 九相电压源逆变器的拓扑图Fig．1 Topology of a nine-phase voltage inverter

九相逆变器空间电压矢量经过坐标变换可分为d1-q1、d3-q3、d5-q5、d7-q7和零序子空间，（本文提到的d－q平面实际为基于定子静止坐标系的α-β平面）其在各个 d-q子空间内的分布［9－10］可分别表示为

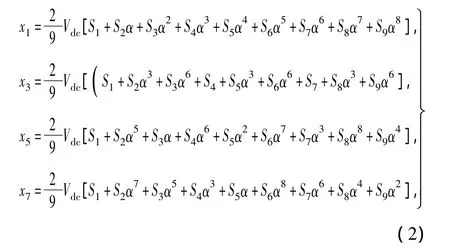
其中α=exp（j2π/9）。九相逆变器一共有29=512个空间电压矢量，包括两个零矢量（000000000和111111111）和510个非零电压矢量。非零电压矢量可以根据负载电路结构分成4组，4-5，3-6，2-7和1-8组，每一组又能根据逆变器相邻桥臂导通的数目进一步分解。如18个最外围的空间矢量是由4或5个导通的相邻开关合成，这些开关矢量形成了d1-q1平面上4-5结构中最大幅值矢量组，称为{4，5}max，同理 3-6，2-7，1-8 结构中，在 d1-q1平面上也同样分别存在18个最大幅值的空间矢量组，称为{3，6}max，{2，7}max和{1，8}max。这 4 个子集在 d1-q1、d3-q3、d5-q5、d7-q7平面的空间分布如图 2 所示。

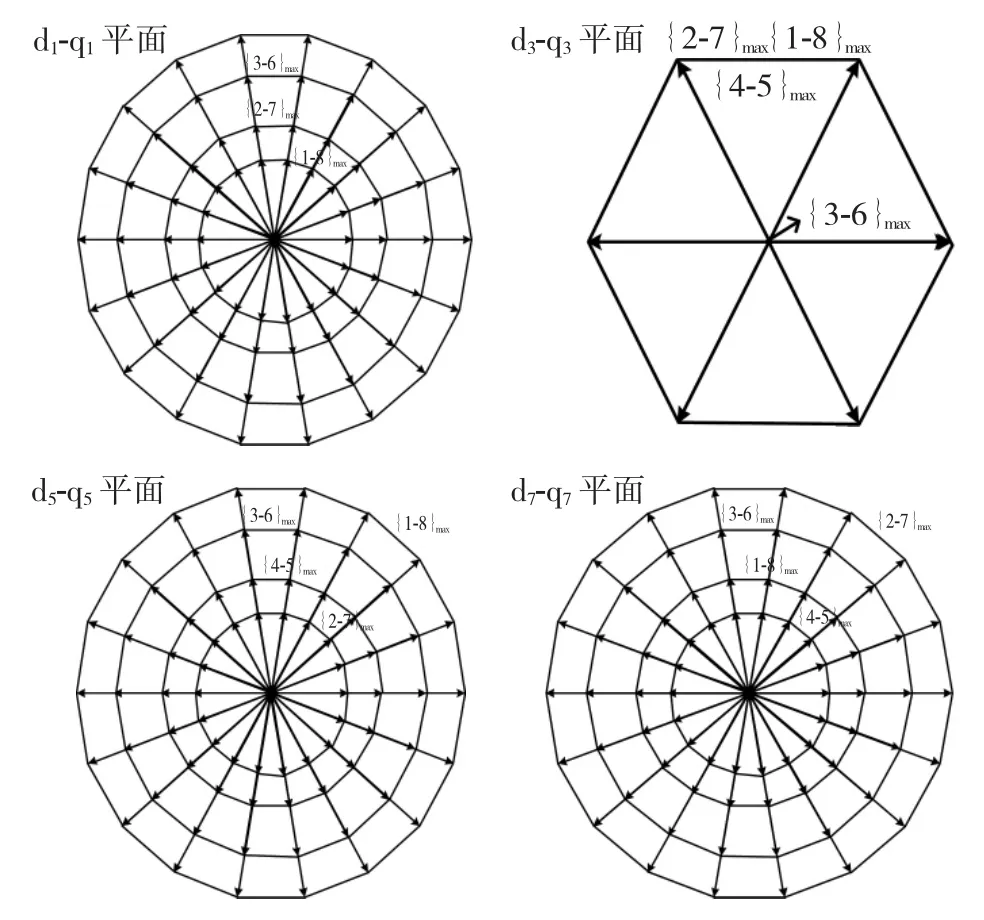
图2 九相逆变器空间电压矢量4个最大幅值子集在各d-q平面的空间分布Fig．2 Four maximum voltage vector subsets corresponding to inverter configurations in four d-q planes

2 非正弦空间电压矢量PWM数学模型

九相逆变器空间矢量脉宽调制的目标是在一个开关周期内给定4个d-q平面的参考电压矢量平均值（¯1ref¯3ref，¯5ref¯7ref），得到相对应的相对于逆变器中点的九个相电压（V1，V2，…，V9）。本文选择8个非零空间电压矢量去合成4个d-q平面的参考电压矢量。为了减小开关损耗和电流纹波，这8个非零空间电压矢量应尽可能的接近参考电压矢量，且每个空间电压矢量中的1或者0都是连续的，即不会出现1或0相隔出现的情况，这样可以保证空间电压矢量方向一致，不会出现定子磁通相互抵消的情况;因此8个非零空间电压矢量应从{4，5}max，{3，6}max，{2，7}max和{1，8}max这 4 个子集中选取。这 8个空间电压矢量的排序按照每次只有1个开关状态变化的原则，从零矢量（000000000）到（111111111），在每个开关周期的前半段电压空间矢量从v0－v9变化，后半段从v9－v0变化，如表1所示［11－12］。

表1 非正弦SVPWM选取的空间电压矢量在d1-q1平面18个扇区中的开关顺序Table 1 Switching table of proposed NSVPWM control strategy for all the 18 sectors on plane d1-q1

九相逆变器空间电压矢量4个最大幅值子集在4个d-q平面上的空间分布共对应着10种不同的电压幅值（VA，VB，VC，VD，VE，VF，VG，VH，VI，VL），可以用 Vdc分别表示为 0.077 Vdc，0.118 Vdc，0.145 Vdc，0.195 Vdc，0.222 Vdc，0.299 Vdc，0.340 Vdc，0.418 Vdc，0.563 Vdc，0.640 Vdc［13］。

在d1-q1平面上4个空间电压矢量最大幅值子集对应着4 个十八边形，幅值分别为 VE，VH，VI，VL，在d5-q5、d7-q7平面上同样对应着4个十八边形，其幅值分别为 VA，VC，VD，VE和 VB，VE，VF，VG，在 d3-q3平面上则对应着一个六边形，幅值为VE，如图2所示，d1-q1平面可被分成18个扇区，每个扇区相隔π/9。以第一扇区为例，按表1选择的8个非零电压空间矢量和2个零矢量在各d-q平面的空间分布如图3所示。

图3 d1-q1平面第一扇区中选取的空间电压矢量在各d-q平面上的空间分布Fig．3 Space distribution of space voltage vectors selected from Sector 1 of plane d1-q1on each plane d-q

在每个d-q平面，参考电压矢量vkref（k=1，3，5，7）可由两个矢量 vαk和 vβk合成［4］为

设逆变器的开关周期为Ts，选取的8个非零空间电压矢量的作用时间分别为 t1，t2，t3，t4，t5，t6，t7，t8，零矢量{000000000}和{111111111}的作用时间分别为 t0和 t9，取 δk=tk/Ts（k=0，1，…，9），如图 3 所示，由伏秒平衡原理可得

联立式（3）、（4）、（5）、（6）可得

从式（8）可以看出，零矢量{000000000}和{111111111}的作用时间没有唯一解，因此存在一个自由度，即两个零矢量的任意分配。根据不同的控制目标如减小开关损耗、优化电流纹波等，选取不同的零矢量分配，便可得到不同的脉宽调制策略，取δ0=δ9，得到NSVPWM，此时各相功率管的驱动信号如图4所示。而特殊情况如v3ref=0，v5ref=0，v7ref=0，则得到SSVPWM。

图4 各相功率元件在扇区1内的导通时间Fig．4 Conducting time for each power device on Sector 1

3 NSVPWM与谐波注入PWM的内在联系

定义脉宽调制度m=Vm1/Vdc，其中Vm1为基波相电压幅值。NSVPWM中各参考电压矢量在相对应d-q平面上的轨迹是半径分别等于m1、m3、m5和m7的圆。在d1-q1平面，以第一扇区为例，如图5所示，由矢量图可求得

m1、m3、m5和m7等价于谐波注入PWM中的各次谐波电压（电流）含量。令 m3=0，m5=0，m7=0（等价于谐波注入PWM中3、5、7次谐波电压（电流）含量为0），若 δ0=δ9=0，此时 d1-q1平面的脉宽调制度m1达到最大值。由式（11）可得此时m1max≈0.508，等价于谐波注入PWM中的正弦基波叠加一个相位相反、幅值为基波幅值1.93%的九次谐波。

图5 参考电压矢量V1ref在d1-q1平面上的轨迹Fig．5 Trajectory of reference voltage V1refon plane of d1-q1

4 NSVPWM各参考电压矢量给定

九相逆变器NSVPWM利用4个d-q平面上的参考电压矢量使电机输入电压波形为平顶波，来提高铁心利用率。在式（10）中令 δ1=δ3=δ7=0，即只采用d1-q1平面上的最大矢量集{4，5}max进行调制，可得此时m1max≈0.632;因此NSVPWM参考电压矢量V1ref在d1-q1平面上的轨迹半径应介于0.508和0.632之间，即0.508＜m1＜0.632，在此限制条件下由式（11）可求得m3、m5和m7的范围，例如

当仅采用d1-q1平面上最大矢量集{4，5}max调制时，此时m3取到负的最小值，即m3min≈－0.192;当仅采用 d1-q1平面上的{3，6}max和{2，7}max矢量子集调制时，由

可得0.169＜δ7＜0.265，代入式（12）可得 m3正的最大值 m3max=0.102，故 －0.192＜m3＜0.102。同理可求得m5、m7的取值范围，即

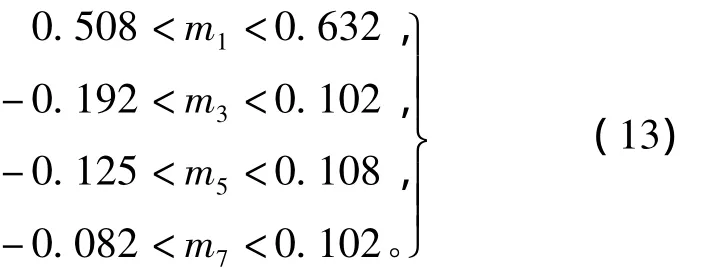
负号等价于谐波注入PWM中谐波相位与基波相位相反。为与SPWM合理比较，应保持两种情况下电机齿、轭部磁密幅值分别相等［14］;因此在满足电机齿、轭部磁密幅值分别相等的前提下，在式（13）所限制的范围内进行遍历寻优，可以得到满足要求的数组平顶波系数，例如 m1=0.526，m3=－0.023，m5= －0.075，m7= －0.026，此时电机输入电压波形如图6所示的平顶波。

图6 采用NSVPWM时的电机输入电压波形Fig．6 Voltage waveforms of motor with NSVPWM

5 试验结果及其分析

为了验证上述理论，构建了一台多相感应电机变频调速系统，控制芯片采用TI公司的32位浮点DSP TMS320C28335和Altera公司的FPGA（现场可编程门阵列 Fieldprogrammablegatearray）EP1C6Q240C6，其中DSP用于算法处理，FPGA用于产生PWM驱动信号。在该变频调速系统下，以一台九相集中整距绕组感应电机为例，分别采用SPWM、SSVPWM和NSVPWM控制策略。

图7和图8分别为采用SSVPWM和NSVPWM控制策略时，额定负载下各d-q平面上的定子电流轨迹。图9为采用NSVPWM时，额定负载下的a相参考电压和定子电流。

图7 采用SSVPWM时各d-q平面上的电流轨迹Fig．7 Trajectory of stator current on each d-q plane with SSVPWM under rated load

图8 采用NSVPWM时各d-q平面上的电流轨迹Fig．8 Trajectory of stator current on each d-q plane with NSVPWM under rated load

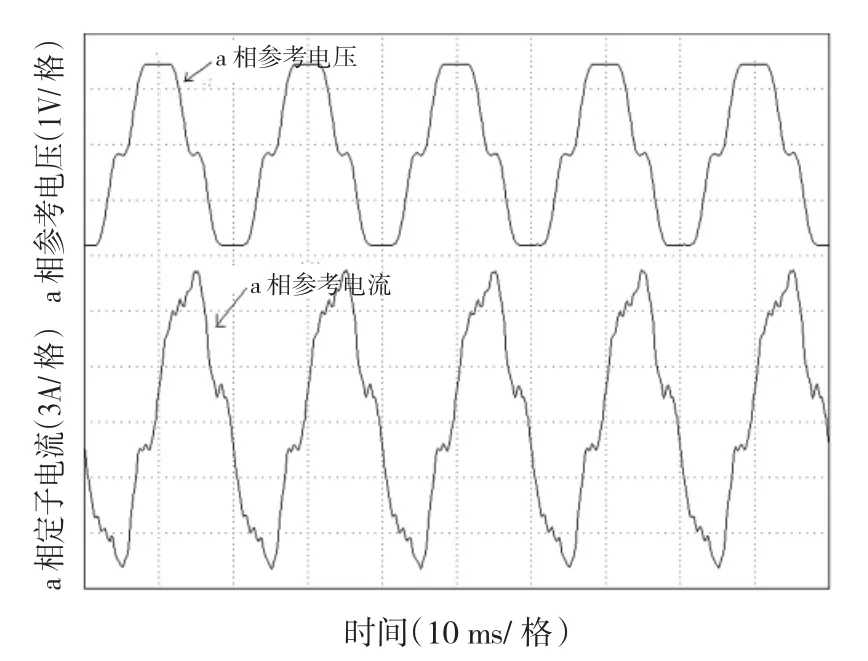
图9 采用NSVPWM时的a相参考电压和定子电流Fig．9 Reference voltage and stator current of phase a with NSVPWM under rated load

图10是保持齿、轭部磁密幅值分别相等、定子铜耗相同时，九相集中整距绕组感应电机分别在SPWM、SSVPWM和NSVPWM三种控制策略下的输出转矩。可以看出:采用SSVPWM时，九相集中整距绕组感应电机输出转矩比采用SPWM时提高了约1.46%;采用NSVPWM时，电机输出转矩比采用SPWM时提高了约6.42%。

图10 三种控制策略下的电机输出转矩比较Fig．10 Comparisons of motor output torques under three kinds of control strategies

多相集中整距绕组感应电机采用NSVPWM控制策略时，电机输出转矩提高的原因主要有两点:①采用NSVPWM控制策略时，谐波电流产生的谐波磁场会减小气隙磁密的幅值，要保证气隙磁密幅值相等，则基波电压应相应增大，直流母线电压利用率提高，输出转矩增大;②谐波电流也产生正的稳定的转矩。前者是采用NSVPWM控制策略时多相集中整距绕组感应电机输出转矩提高的主要原因。

6 结论

提出了一种输出非正弦电压的空间电压矢量PWM（NSVPWM）的控制策略，并应用于1台九相集中整距绕组感应电机上。试验结果表明，采用NSVPWM控制策略时，额定负载下九相集中整距绕组感应电机输出转矩比采用SPWM时提高了约6%。但这种非正弦供电技术在电机轻载时不利，如何在线选择合适的供电技术是下一步需要解决的问题。

［1］SINGH G K．Multiphase induction machine drive research:a survey［J］．Electronic Power System Research，2002，61（2）:139 －147．

［2］LEVI E．Multiphase electric machines for variable speed applications［J］．IEEE Trans．on Industrial Electronics，2008，55（5）:1893－1909．

［3］TOLIYAT H A，SHI R，XU H．A DSP-based vector control of five-phase synchronous reluctance motor［J］．IEEE Trans．on Industry Applications，2000，4（2）:432 －437．

［4］GRANDI G，SERRA G，TANI A．Space vector modulation of a nine-phase voltage source inverter［J］．IEEE International Symposium on Industrial Electronics，2007，3（1）:431 －436．

［5］HYUNG M R，JANG H K，SEUNG K S．Synchronous frame current control of multiphase synchronous motor（Part I）:modeling and current control based on multiple d-q spaces concept under balanced condition［C］∥39th IAS Annual Meeting．United States:IEEE Press，2004:56 －63．

［6］TOLIYAT H A．Analysis and simulation of five-phase synchronous reluctance machines including third harmonic of air-gap MMF［J］．IEEE Trans．on Industrial Electronics，1998，34（2）:332－339．

［7］TOLIYAT H A．Analysis of a concentrated winding induction machine for adjustable speed drive applications（Part I）:motor analysis［J］．IEEE Trans．Energy Conversion，1991，6（4）:679－683．

［8］薛山，温旭辉．一种新颖的多相SVPWM［J］．电工技术学报，2006，21（2）:68－72．

XUE Shan，WEN Xuhui．Novel multiphase SVPWM［J］．Transactions of China Electrotechnical Society，2006，21（2）:68－72．

［9］薛山，温旭辉，王又珑．多相永磁同步电机多维控制技术［J］．电工技术学报，2008，23（9）:65－69．

XUE Shan，WEN Xuhui，WANG Youlong．Multi-dimensional control in multiphase permanent motor drives［J］．Transactions of China Electrotechnical Society，2008，23（009）:65 －69．

［10］KELLY G W，STRANGAS E G，MILLER J H．Multiphase space vector pulse width modulation［J］．IEEE Trans．Energy Conversion，2003，18（2）:259－264．

［11］王晓刚，谢运祥，黄少辉，等．四桥臂逆变器SPWM和SVPWM的归一化研究［J］．电机与控制学报，2010，12（1）:23－28．

WANG Xiaogang，XIE Yunxiang，HUANG Shaohui，et al．Unification of SPWM and SVPWM in four-leg inverter［J］．Electric Machines and Control，2010，12（1）:23 －28．

［12］赵品志，杨贵杰，刘春龙．五相电压源逆变器 SVPWM优化算法［J］．电机与控制学报，2009，13（4）:516－522．

ZHAO Pinzhi，YANG Guijie，LIU Chunlong．Optimal SVPWM algorithm for five-phase VSI［J］．Electric Machines and Control，2009，13（4）:516－522．

［13］张成胜，张晓锋，乔鸣忠，等．基于SVPWM五相感应电机直接转矩控制研究［J］．电机与控制学报，2008，12（3）:304－308．

ZHANG Chengsheng， ZHANG Xiaofeng， QIAO Mingzhong，et al．SVPWM method of five-phase induction motor direct torque control［J］．Electric Machines and Control，2008，12（3）:304－308．

［14］康敏，黄进．大功率多相感应电机的非正弦供电技术［J］．大电机技术，2006，12（9）:20－24．

KANG Min，HUANG Jin．Technology of non-sinusoidal source fed high power multiphase induction machines［J］．Large Electric Machine and Hydraulic Turbine，2006，12（9）:20－24．

（编辑:张静）