基于反馈神经网络的电压暂降特征量实时检测方法

李承， 杨博， 邹云屏， 丁洪发

（1．华中科技大学电气与电子工程学院，湖北武汉 430074;2．中南财经政法大学信息学院，湖北武汉 430074）

0 引言

近年来，输电系统和配电系统中存在的电压暂降、三相不平衡、高次谐波等电能质量问题，越来越受到人们的关注，而电压暂降所带来的问题以及补偿电压暂降的方法，已经成为专家学者研究的热点问题之一［1－4］。电压暂降对于那些对电压敏感的用户危害较大，如半导体制造业、造纸业、纺织业等。在生产自动化程度日益完善和普及的今天，即使是连续生产过程中的某一台设备感受到电压暂降也可能使整个生产线停运，导致生产出次品或废品，造成巨大的经济损失;因此，电压暂降给高技术含量的用电设备带来的严重影响与危害表现得十分突出［5－7］。

动态电压恢复器（DVR）是解决电压暂降问题的一种有效方法［8－9］，它能快速向系统注入正常电压和故障电压之差，补偿电压暂降，因而对电压暂降特征量（如暂降幅值、起止时刻和相位跳变）的快速、准确检测是电压暂降补偿的前提［10］。目前，对电压暂降的检测已有不少方法，例如:有效值计算方法、峰值电压法、基波分量法都只能用于检测电压暂降的幅值;单相电压变换平均值法、瞬时电压d-q分解法能同时检测电压暂降的幅值和相位跳变;基于瞬时无功功率理论的d-q-0变换方法是目前DVR装置中常用的电压暂降检测方法，但是该方法只适用于三相对称情况，而且没有考虑电压暂降时可能伴随的相位跳变问题。由于实际中常有单相短路故障所引起的不对称电压暂降，后者需首先由单相电压构造出虚拟三相系统才能进行检测，原理上不够简单明了，实现过程中仍需进行三相变换，计算量仍然较大;而且，检测波形会出现短时扰动，影响检测精度。

文中提出了基于反馈型神经网络的电压暂降检测方法，该方法利用反馈神经网络实现了在误差最小条件下的电压暂降检测，建立了检测模型，提高了检测精度并利用Matlab/Simulink进行了仿真实验。由于神经网络具有并联、分布工作的特点，该方法为实现电压暂降特征量的快速、准确检测提供了一种有效途径。

1 实时电压暂降检测模型

1.1 基本反馈神经网络检测模型

设接有DVR的供电系统电源侧端电压为

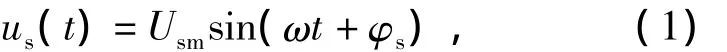
其中Usm和φs分别为电源侧端电压的幅值和初相位，也是神经网络需要检测的主要特征量。

设神经网络输出端的输出电压为

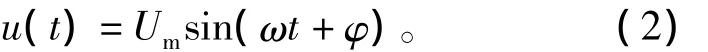
实际中，希望神经网络检测到的电压u（t）与电源电压us（t）充分接近，均方误差最小;因此，神经网络输出电压u（t）的特征量Um和φ与电源电压us（t）的特征量Usm和φs也有最小均方误差。

利用三角关系，式（2）可以改写为

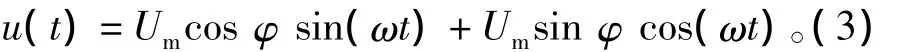
令

如果在t时刻电源电压为us（t），神经网络网络输出电压为u（t），而实际中，希望网络输出电压u（t）与电源电压（期望输出）us（t）之间在任意时刻都有最小误差。显然，要使u（t）与 us（t）之间在任意时刻都有最小误差，只要u（t）的特征量Um和φ与电源电压us（t）的特征量Usm和φs有最小误差就可以了。根据式（5）可知，只要得到A、B两个量，也就得到了Um和φ;因此，u（t）与 us（t）之间在任意时刻都有最小误差问题转化成了检测A、B两个量的问题，只要检测到A和B，再根据式（5）和式（6）就可得到电压u（t）。而且此时得到的u（t）与us（t）之间在任意时刻都有最小误差。为此设网络的误差函数

显然，指标函数E（t）是向量X的函数。

如果把A、B作为网络运行中的状态，而把E（t）作为网络的能量函数，反馈型神经网络运行的特点就是随着网络状态的不断变化，其能量逐渐减小。也就是说，网络运行时，其状态的变化是朝着网络能量减小的方向运行。而网络运行中网络的保持权值不变;因此，根据反馈型神经网络基本原理［11－12］，网络运行时，随着参数（状态）X（A、B）的调整变化，其指标函数E（t）应该朝着减小的方向变化，即有

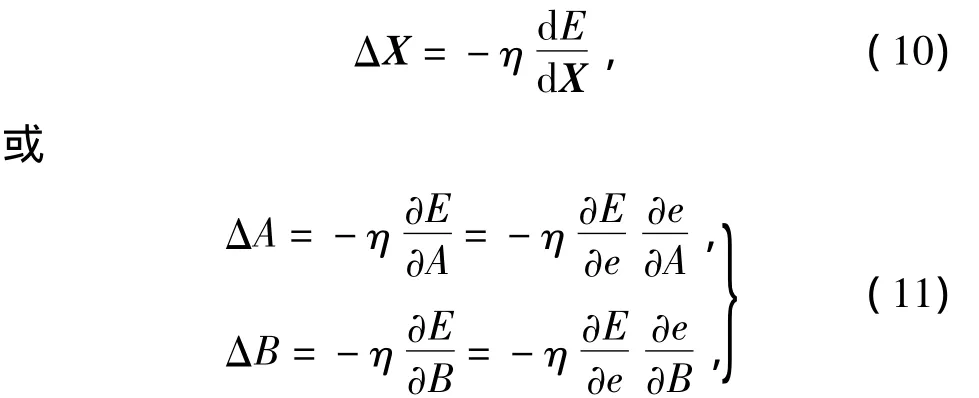
式（10）、（11）中，η为网络状态转换速率，它会影响网络运行速度与稳定性，一般是一个小正数。

图1 电压暂降实时检测模型Fig．1 Voltage sag real-time detection model

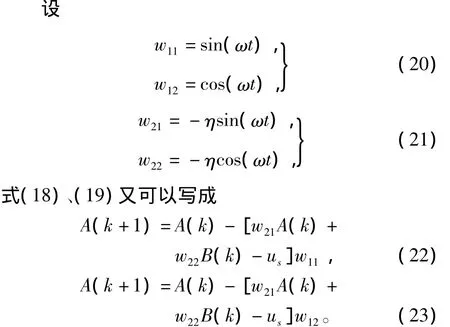
由式（22）、（23）也可以把网络改画为图2的形式。

在该模型中，w11、w12、w21、w22为网络权值，A、B为网络状态，us为网络输入。网络运行中，其权值不变（不依状态变化而调整）。网络的状态A、B会随网络运行快速调整，并且状态的调整始终朝着u（t）与us（t）有最小均方误差的方向进行。

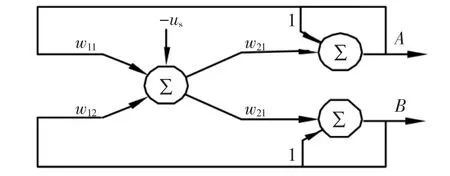
图2 电压暂降实时检测模型另一种形式Fig．2 Other model of voltage sag real-time detection

在该网络中，只要输入电源电压us（t），就可以实时检测到相应的特征量。当电压发生暂降时，网络可以快速检测到暂降发生时刻，得到输出值A、B，然后由式（6）实时得到电压的幅值Um和初相位φ。网络实时输出u（t）的特征值与期望电压us的特征值之间在任一时刻都有最小均方误差。由于神经网络并行运算特征，使检测具有很好的实时性。

1.2 延迟平均反馈神经网络检测模型

上述网络对每一时刻电压都会计算出相应的特征值;但是，如果信号本身有干扰，网络的输出误差就会曾大。换句话说，网络输出的稳定性易受信号干扰的影响，为此，可以采用延迟平均方法来提高网络检测的抗干扰能力，提高检测准确性与稳定性。具体方法是在一个很短的时间内，把信号进行N次延时，并把各延迟的信号送入网络中，经网络运行得到总均方误差作为网络能量函数。

设t时刻网络输出u（t）与电源电压（期望输出）us（t）的误差为

根据神经网络的理论可知，反馈型神经网络运行时，随着状态A、B不断变化，网络的能量会逐渐减小，即E（t）是状态A、B的函数，并随A、B变化逐渐减小，因此有

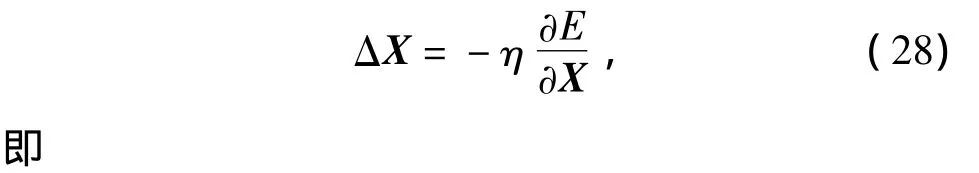
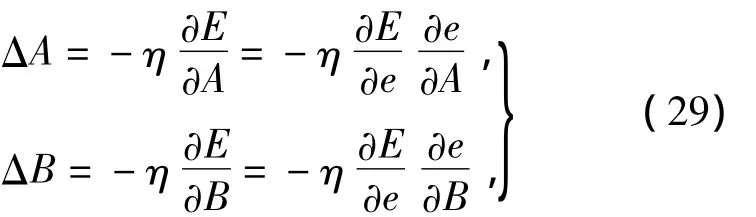
网络状态转换速率η影响着网络的运行速度，也对稳定性有直接影响。

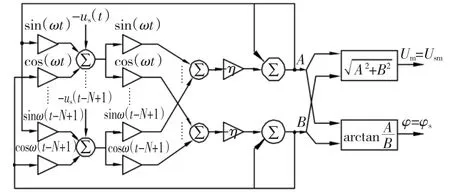
图3 延迟平均电压暂降实时检测模型Fig．3 Average delay model of detecting voltage sag

如果设

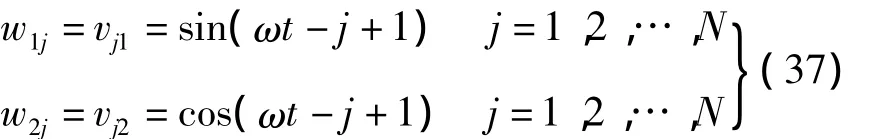
其中 w1j、w2j、vj1、vj2分别为网络的权值，他们不是网络状态A、B的函数;所以，反馈型网络运行时，其权值不随状态变化，但状态变化会引起网络能量下降。

根据式（37），图3所示的网络也可以改为图4的形式。

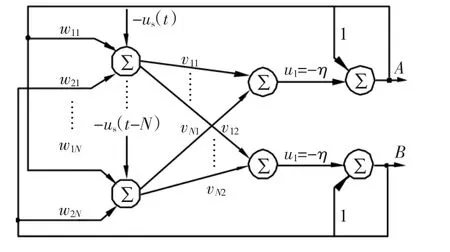
图4 延迟平均电压暂降实时检测模型另一种形式Fig．4 Other average delay model of detecting voltage sag

在图3或图4的反馈网络模型中，只要将延迟值us（t）～us（t－N+1）输入到网络，网络即可以快速运行，并得到状态值A、B。由A、B可以容易地得到电压u（t）的特征量幅值Um和相位φ。网络运行可以保证网络输出与时间电源特征量之间有最小误差。

2 仿真实验与结果分析

为了验证以上理论分析结论的正确性与有效性，本节对所建立的网络模型进行仿真实验并分析了仿真实验结果。对图1或图2所示的基本检测模型和图3或图4所示的延迟平均检测模型分别给出仿真实验结果和具体分析。

2.1 基本检测模型仿真实验结果与分析

对图3所示的基本检测模型，取η=0.2，其他仿真实验参数分别为仿真时间为电源电压的20个周期，即0.4 s;电源电压正常时为us（t）=220sin（100πt）V，在0.05～0.15 s和0.25～0.35 s间;电源电压两次发生暂降，暂降的幅度为50%，即降为us（t）= 110sin（100πt）V;幅度发生暂降时，不伴随相位变化，即Δφ=0o。仿真波形如图5所示。

结果分析:

1）从仿真实验波形可以看到，基本反馈神经网络检测模型有非常快的响应速度，这一点从电源发生跃变时检测到的幅值波形可以看到。在0.05、0.15、0.25和0.35 s处，检测到的电压幅值几乎瞬间完成跃变，这是由于模型中有强烈的正反馈，正反馈过程加快了检测速度。

2）正是由于强烈的正反馈，网络检测是瞬时完成的，同时也带来稳定性问题。当网络受到一点点扰动，就可以造成了网络运行不稳定。从检测到的幅值和相位可以看到，在0～0.04 s和0.25～0.28 s之间，无论是幅值还是相位都不稳定，出现振荡现象。当然，网络在0.15和0.35 s时，信号也出现跳变，但没有出现振荡，其原因还有待进一步研究。

3）当幅值发生暂降的同时伴有相位跳变时（未给出仿真实验波形），网络运行更为不稳定，几乎不能得到正确检测结果。

综上所述，采用图4所示的延迟平均检测模型可以有效地解决稳定性问题。

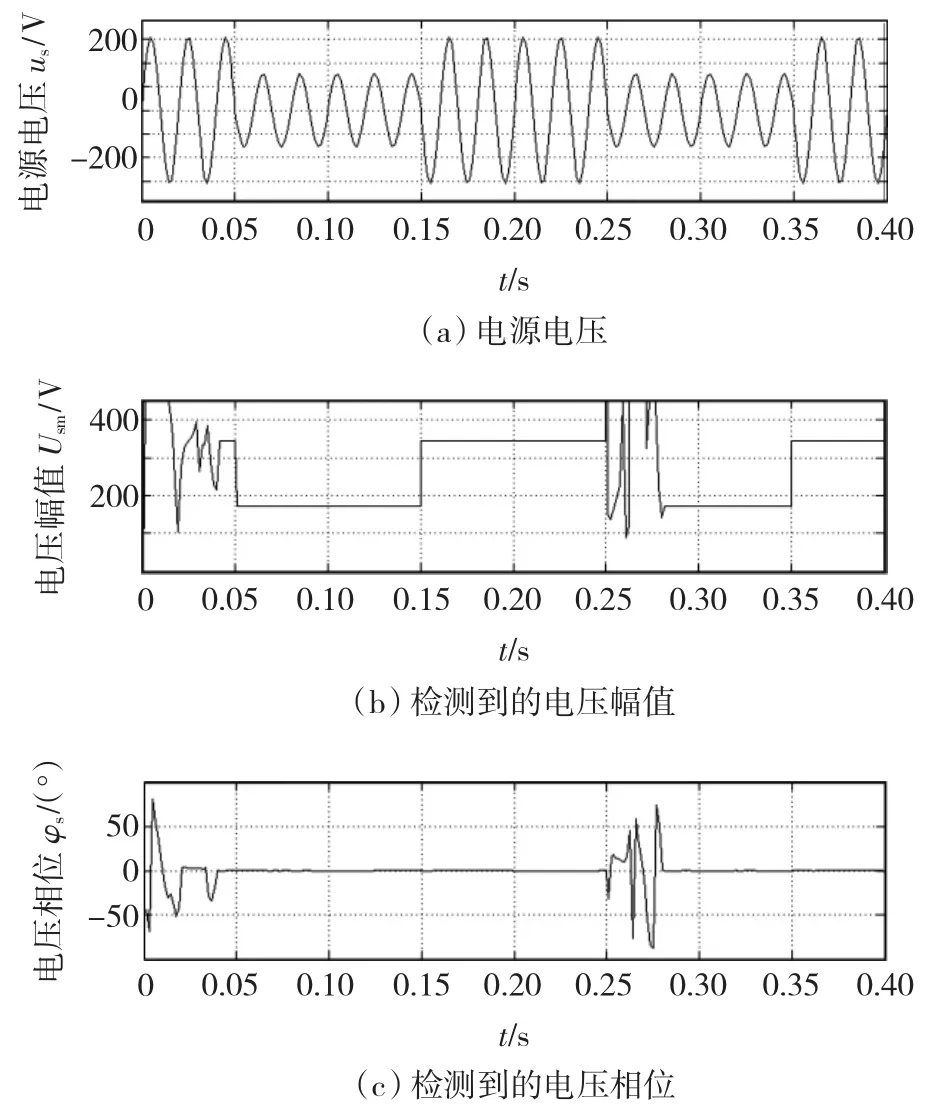
图5 Δφs=0时的仿真结果Fig．5 Waveforms of simulation at Δφs=0

2.2 延迟平均反馈神经网络仿真实验结果与分析

采用图3或图4所示的延迟平均检测模型进行仿真实验，仿真实验条件分别为η=0.11，N=2，延迟时间Δt=1×10－8s，其他仿真实验参数分别为仿真时间为电源电压的20个周期，即0.4 s;电源电压正常时为us（t）= 220sin（100πt）V，在 0.05～0.15 s和0.25～0.35 s间;电源电压两次发生暂降，暂降的幅下降为原来幅值的50%，即降为us（t）=110■ 2sin（100πt）V。在幅度发生暂降时，对相位变化分别为 Δφs=0°、Δφs=45°和 Δφs=90°的 3 种情况进行了仿真，仿真波形如图6、图7和图8所示。

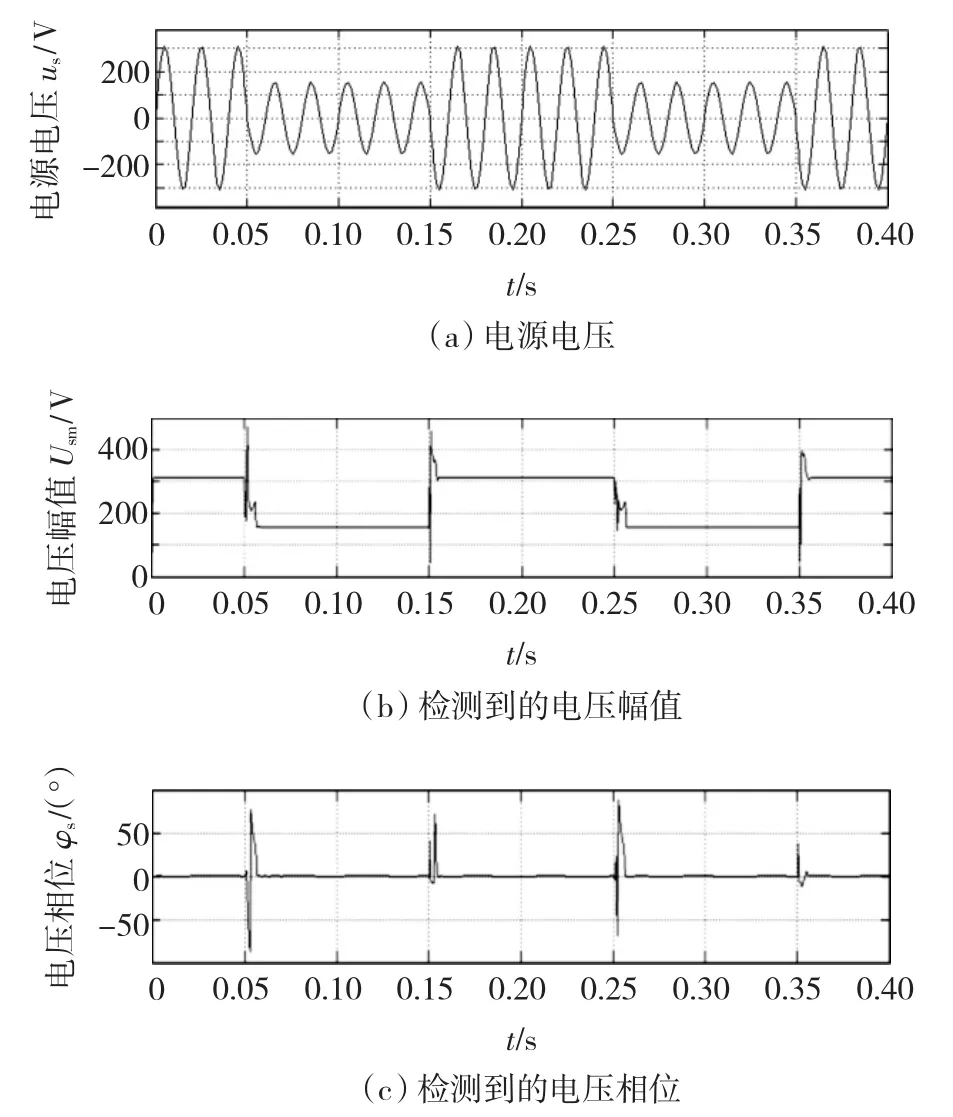
图6 Δφs=0°时的波形Fig．6 Waveforms of simulation at Δφs=0°

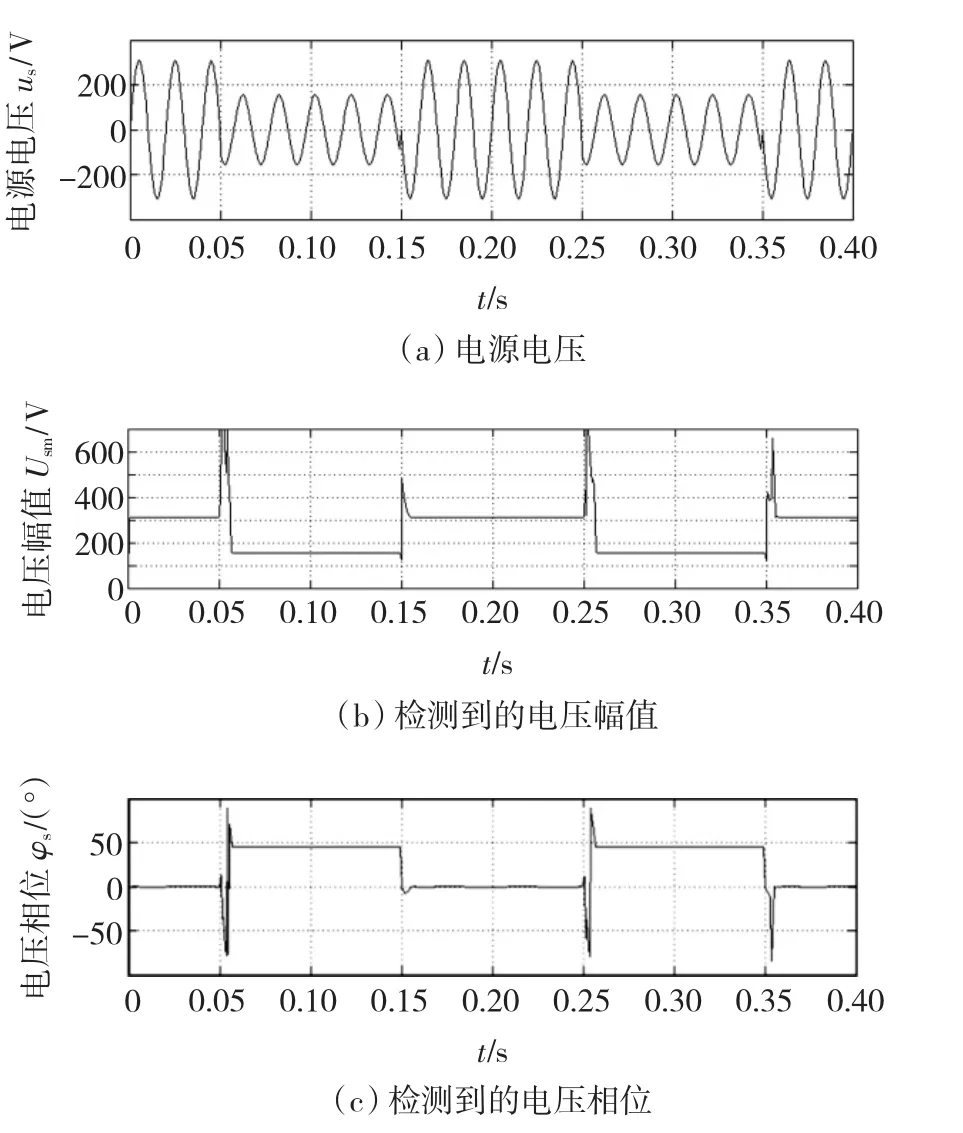
图7 Δφs=－45°时的波形Fig．7 Waveforms of simulation at Δφs= －60°

由图6、图7和图8可以看到:

1）网络实时得到的波形与理论分析一致。对于电源电压us发生暂降并伴有相位不同的变化（φs分别为 0°、60°、90°），网络都可以实时地检测到电压暂降的幅值与相位。

2）仿真实验波形还可以看到，网络对电压暂降的检测不仅有很好的静态精度，也有快速的动态跟踪与响应能力。

3）延迟平均检测模型比基本检测模型运行时稳定性要好，这表现为电压跳变时，检测结果振荡小得多。

4）在电压跳变时，网络检测结果出现短暂的暂态尖峰过程，但时间很短，最长不超过5 ms。

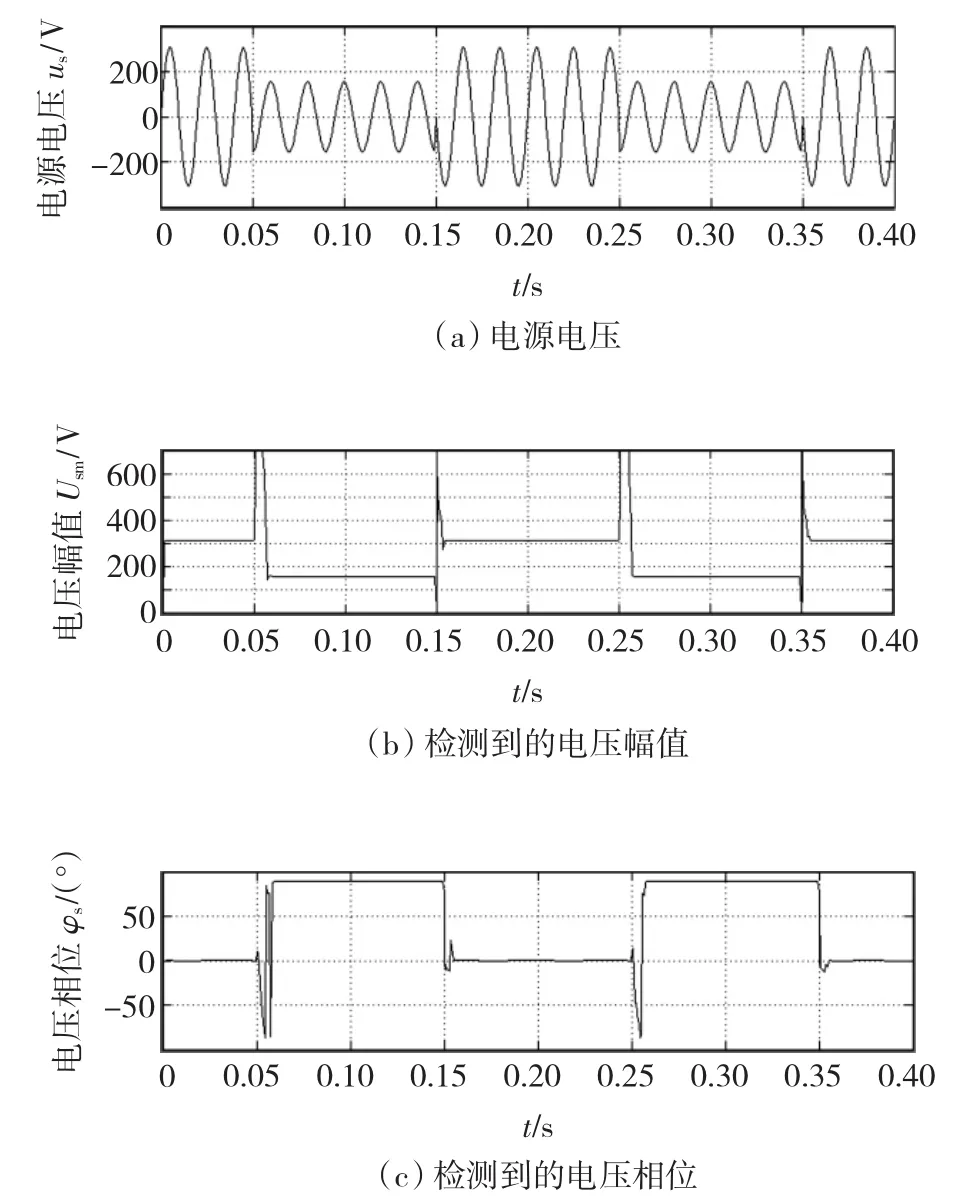
图8 Δφs=－90°时的波形Fig．8 Waveforms of simulation at Δφs= －90°

产生尖峰过程的原因在于网络对信号的微分把跳变大大地放大了。从式（11）和式（29）可以知道，网络的输出A、B在模型中做了微分运算，而A、B直接生成电压幅值Um和相位φs。当幅值和相位发生跳变时，A、B也发生跳变，加之微分运算，此时会产生较大的ΔA、ΔB;因此，在仿真波形中引起尖峰过程是必然的。

尽管网络检测过程已经很快，但要是能够去掉尖峰过程，还可以进一步提高检测速度，缩短检测所需的时间。

另外，当供电电源中有谐波时，检测结果会有误差。图9所示为供电电压包含4%的3次谐波和1%的5次谐波时的仿真结果。图9中可见，检测到的幅值和相位都有波动。

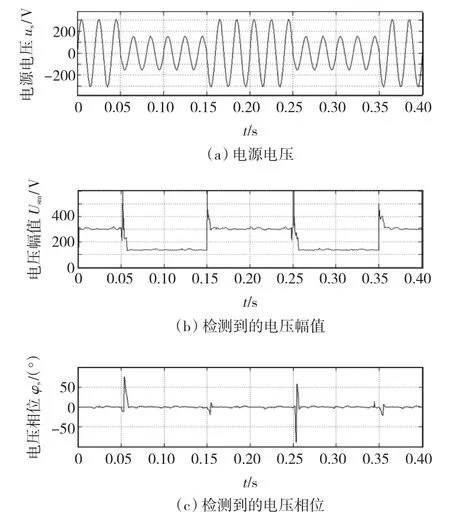
图9 电源中包含3次和5次谐波，Δφs=0°时的波形Fig．9 Waveforms of simulation at Δφs=0°with 3rd and 5th harmonics in supply voltage

3 结论

对于本文提出的基于反馈神经网络的电压暂降实时检测模型，从理论分析论证和仿真实验验证，可以得到以下结论。

1）本文提出的两种基于反馈型神经网络电压暂降实时检测模型原理正确，方案可行。

2）两种检测模型中，延迟平均具有较好的稳定性。对幅值暂降同时伴有相位跳变等情况，能够快速检测到电压暂降的特征值。

3）网络运行过程中，始终可以满足均方误差最小条件下的电压暂降检测，动态响应快、稳态精度高。

4）由于神经网络的并行运算能力非常强，使检测实时性好。仿真实验的波形表明，检测动态过程小于5 ms。

对于如何消除电压暂降时出现的尖峰过程问题，还有待进一步研究与改进。如能够去掉尖峰过程，还可以进一步提高检测速度，缩短检测所需的时间。

［1］WOODLEY N H，MOORGAN L，SUNDARAM A．Experience with an inverter-based dynamic voltage restorer［J］．IEEE Trans．on Power Delivery，1999，14（3）:1181 －1186．

［2］EDWARD R W．Power quality issues-standard and guidelines［J］．IEEE Trans．on Industry Application，1996，32（3）:625 －632．

［3］姜齐荣，沈斐，韩英铎．现代电能控制技术［J］．电力电子技术，2004，38（6）:1－7．

JIANG Qirong，SHEN Fei，HAN Yingduo．Development of modern custom power technology［J］．Power Electronics，2004，38（6）:1－7．

［4］李承，邹云屏，范婕．动态电压恢复器单周控制的建模与仿真研究［J］．电力自动化设备，2006，26（4）:7－10．

LI Cheng，ZOU Yunping，FAN Jie．Modeling and simulation of single-phase DVR based on one-cycle control［J］．Electric Power Automation Equipment，2006，26（4）:7 －10．

［5］XIAO Xiangning，XU Yonghai，LIU Liangguang．Simulation and analysis of voltage sag mitigation using active series voltage injection［C］∥Proceedings of the2000International Conference on Power System Technology（POWERCON2000）．Perth，Australia:IEEE，2000:1317－1322．

［6］肖湘宁，徐永海．电能质量问题剖析［J］．电网技术，2001，25（3）:66－69．

XIAO Xiangning，XU Yonghai．Power quality analysis and development［J］．Power System Technology，2001，25（3）:66 －69．

［7］肖湘宁，徐永海，刘昊．电压凹陷特征量检测算法研究［J］．电力自动化设备，2002，22（1）:19－22．

XIAO Xiangning，XU Yonghai，LIU Hao．Research on the detection method of voltage sag characteristics［J］．Electric Power Automation Equipment，2006，26（4）:7 －10．

［8］KARA A，DAHLER P．Power supply quality improvement with a dynamic voltage restorer（DVR）［C］∥Thirteenth Annual Applied Power Electronics Conference and Exposition（APEC'98）．Anaheim，CA，USA:IEEE，1998:986－993．

［9］李承，林红，杨红权．基于三相全桥逆变器的DVR单周控制策略研究［J］．电力自动化设备，2007，27（6）:8－12，21．

LI Cheng，LIN Hong，YANG Hongquan．Study on one-cycle control of DVR based on three-phase full-bridge inverter［J］．Electric Power Automation Equipment，2006，27（6）:8 －12，21．

［10］杨亚飞，颜湘武，娄尧林．一种新的电压骤降特征量检测方法［J］．电力系统自动化，2004，28（4）:41－44．

YANG Yafei，YAN Xiangwu，LOU Raoling．A new method to detect voltage sag characteristics［J］．Automation of Electric Power Systems，2004，28（4）:41－44．

［11］阎平凡，张长水．人工神经网珞与模拟进化计算［M］．北京:清华大学出版社，2000:101－129．

［12］焦李成．神将网络计算［M］．西安:西安电子科技大学出版社，1993:238－245．

（编辑:张静）