三次谐波电压注入的五相感应电机SVM-DTC方法

朱鹏， 张晓锋， 乔鸣忠， 张成胜，2， 蔡巍

（1．海军工程大学 电气工程系，湖北 武汉 430033;2．94878部队，安徽 芜湖 241009）

0 引言

与三相变频调速系统相比，多相系统减小了转矩脉动，降低了对功率器件容量的要求，相数的增加还有利于提高低速区的运行特性。此外，多相H桥系统冗余性好，当多相中的一相或几相发生故障时，通过适当的控制，电机可以降功率运行。五相感应电机系统是其中的典型代表。

感应电机直接转矩控制有控制简单、动态响应快，无需旋转坐标变换和电流调节环节等优点［1］，因而日益受到重视。目前，有关五相感应电机直接转矩控制的研究基本上都是采用基于开关表的滞环控制方法［2－3］，这种方法在开关频率相对较低时，表现出较大的电流和转矩脉动，对电机的低速运行有较大影响。近年来，许多文献提出将采用空间矢量调制技术的直接转矩控制，该方法可以有效减小电流和转矩脉动，提高系统的运行性能［4－5］。

对于采用集中整距绕组的多相感应电机来说，通过非正弦电压和电流供电，可以降低基波磁势及磁密峰值并使得气隙磁密波形为准方波，从而提高铁心材料利用率、转矩密度和功率密度。目前，对于集中整距绕组电机控制，主要采用的是基于转子磁场定向的矢量控制方式［6］。本文将空间电压矢量调制（SVM）与直接转矩控制（DTC）相结合，并根据集中整距绕组的特点，提出了三次谐波电压注入的五相感应电机SVM-DTC方法。由于被控对象为定子磁链和转矩，相对于转子磁场定向的矢量控制方式，该方法具有更好的动、稳态性能，且易于满足气隙磁密波形为准方波的控制要求。

1 三次谐波注入的五相感应电机SVM-DTC原理

1.1 三次谐波注入的五相感应电机直接转矩控制

原理

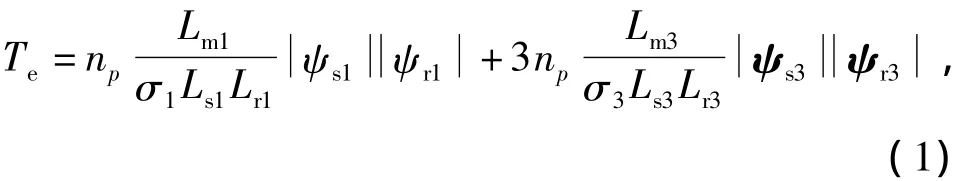
由式（1）可知，如果定子磁链的基波和三次谐波幅值恒定，且 －π/2≤δ1，δ3≤π/2，则通过改变 δ1和δ3可实现对电磁转矩的直接控制，其中δ1为定转子磁链基波分量之间的夹角，δ3为定转子磁链三次谐波分量之间的夹角，称δ1和δ3为转矩角、磁通角或负载角。

根据电机电压方程

其中i=1，3，分别对应基波和三次谐波分量。在忽略定子电阻rs上的压降情况下，定子磁链变化量Δψsi近似为

由式（3）可知，Δψsi的大小与作用于定子的电压矢量大小及其作用时间成正比，且Δψsi的变化方向与该电压矢量的方向一致。

根据电机电压和磁链方程，得

地面三维激光扫描技术在建立三维模型中的应用，主要有两大部分，一是纹理映射，二是模型建立。模型建立是结合点云数据信息来建立的，重点运用3Dsmax形式来构建模型的，保证其标准化。纹理映射主要是采用数码相机，并且安装到扫描仪上，进而搜集大量的纹理信息，科学的建立建筑工程模型。

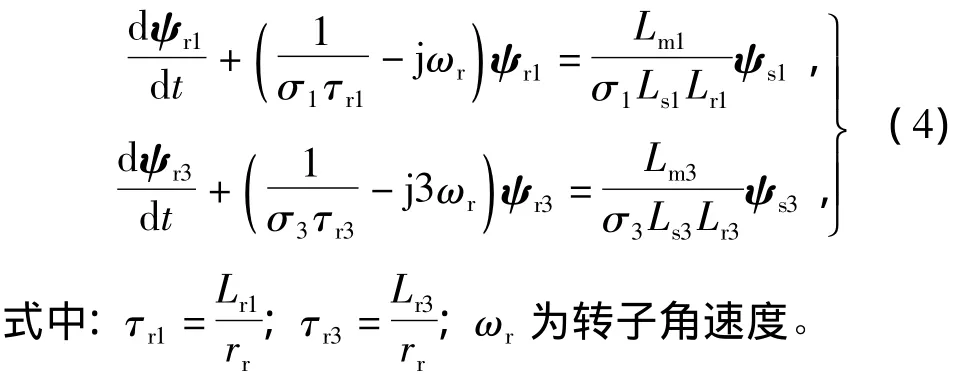
式（4）表明，转子磁链在定子磁链作用下的动态响应具有一阶低通滤波特性。在Δt内，随着定子电压矢量的作用，定子磁链的旋转速度迅速变化，而转子磁链旋转速度保持不变，从而使δ1和δ3迅速改变。

综上所述，五相集中整距绕组感应电机直接转矩控制的原理是，通过改变作用于定子的基波和三次谐波电压矢量，从而同时改变定子磁链基波和三次谐波矢量的夹角以及电磁转矩，使得定子磁链的基波和三次谐波幅值保持恒定，且电磁转矩随负载而变化［4－5］。

1.2 三次谐波电压注入的五相感应电机SVMDTC方法

基于空间矢量调制直接转矩控制的关键在于空间参考电压矢量生成的计算，这个参考电压矢量必须包含转矩控制与磁链控制的信息。图1所示为定子输入电压矢量对定子磁链影响示意图（图1中θs1、θr1为定、转子相绕组磁链基波分量与轴 α1夹角;θs3、θr3为定、转子磁链三次谐波分量与轴 α3夹角;ω为同步角速度）。

图1中，在当前时刻 tk，定子磁链 ψs1、ψs3与转子磁链 ψr1、ψr3之间的夹角分别为 δ1、δ3;下一时刻tk+1，转矩角的变化量Δδ1和Δδ3根据转矩闭环得到，同时考虑定、转子磁链在Δt=tk+1－tk内旋转过的角度以及定子磁链幅值不变，即可得到下一时刻定子磁链矢量和。分别在 α1β1和 α3β3平面进行分解，则定子磁链在Δt内的变化量为

图1 定子电压矢量对磁链的影响Fig．1 Effect of stator voltage vector on stator flux linkage

其中Δt一般选择为一个开关周期Ts。

通过式（9）和（10）得到的参考电压矢量，不仅可以消除转矩误差，同时还可控制定子磁链幅值保持恒定。最后根据参考电压，由SVPWM发生器产生逆变器的触发脉冲。

1.3 三次谐波电压注入的五相感应电机SVMDTC方法的3种实现方案

以上在对五相感应电机SVM-DTC方法的分析中，是将基波和三次谐波分量分开讨论的。下面介绍3种具体实现三次谐波电压注入的方法，协调基波和三次谐波电压之间的关系，使得气隙磁密波形为所要求的准方波，从而提高电机的性能指标。

方法1只对基波电压进行闭环控制，三次谐波电压根据气隙磁密的要求，按基波电压的一定比例给定。图2示出速度环输出为总电磁转矩的给定值T*

e，基波磁场产生的电磁转矩按比例取为=k1，该转矩与观测值的误差经PI调节得到Δδ1，再由定子基波磁链幅值的给定值以及同步转速，可得到基波电压的参考值和 u。三次谐波电压的参考值按比例取为=ku，=ku，其中k1和ku是实现该方法的关键。

图2 三次谐波电压注入的五相感应电机SVM-DTC方法1Fig．2 Five-phase induction motor SVM-DTC Method 1 with third harmonic voltage injection

方法2对基波和三次谐波电压分别进行闭环控制（见图3）。图3中，给定转矩、与观测值Te1、Te3的误差分别经 PI调节得到 Δδ1和 Δδ3，再分别由磁链基波幅值和三次磁链幅值的给定值，根据式（9）和（10）得到基波和三次谐波电压的参考值，其中k1、k3的确定同方法1。

方法2中的Δδ1和Δδ3分别由各自的转矩闭环得到，但由于转矩观测的误差不可避免，导致定子磁链的基波与三次谐波相位关系不断变化。虽然其幅值能保证一定比例，但两者之间不确定的相位关系会造成合成磁密的波形不断变化;因此，需要对方法2进行优化，即方法3——优化方法（具体控制方法见图4）。

图3 三次谐波电压注入的五相感应电机SVM-DTC方法2Fig．3 Five-phase induction motor SVM-DTC Method 2 with third harmonic voltage injection

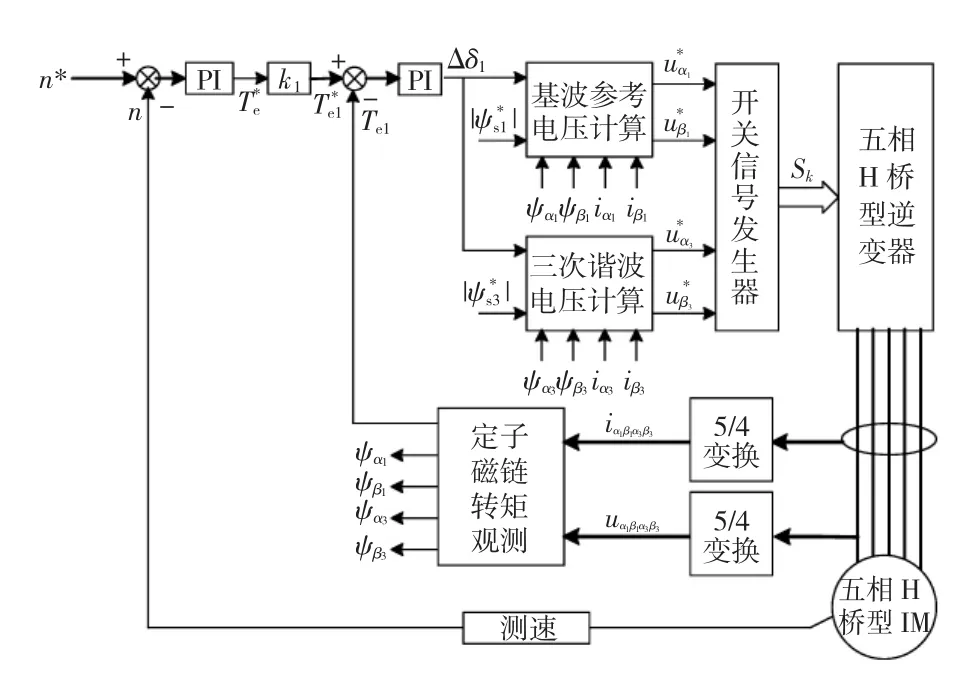
图4 三次谐波电压注入的五相感应电机SVM-DTC优化方法Fig．4 Five-phase induction motor SVM-DTC optimized method with third harmonic voltage injection

在优化方法中，取定子磁链三次谐波分量的转矩角变化量为Δδ3=3Δδ1，这样就保证了磁链三次谐波与基波之间的相位关系恒定。

2 基于电平合成的五相三电平PWM方法

文中驱动五相感应电机逆变器采用三电平H桥型结构，如图5所示。

图5 五相三电平H桥型逆变器主电路Fig．5 Main circuit of five-phase three-level H bridge inverter

逆变器每相H桥的左右桥臂均采用二极管钳位，每个桥臂分别有3个输出状态:上两管导通，下两管截止时，输出电压为Udc/2;中间两管导通，上下两管截止时，输出电压为0;下两管导通，上两管截止时，输出电压为－Udc/2。故每相输出电压为五个电平:±Udc、±Udc/2以及0。为方便分析计算，将每相输出电压以最小电平台阶，即Udc/2为基值进行标幺化，得到每相输出的五个电平:±2、±1以及 0。第 i（i=a，b，c，d，e）相输出电压与开关状态及开关函数的对应关系如表1所示。

表1 相电压与开关状态和开关函数的关系Table 1 Relationships between phase-voltage，switching state and switching function

假设开关周期Ts内第i相参考电压的标幺值为u*i，则在调制比 m∈［0，1］时，u*i必是介于两个相邻电平之间，根据伏秒平衡原则，u*i即可由这两个电平合成。为此，首先要确定与参考相电压相邻的上下两个电平，然后分别计算这两个电平的作用时间，最后根据这两个电平的作用顺序确定开关信号。令两个相邻的上下电平分别为Li+1和Li，且Li=int（u*i），int（）为向下取整运算。电平Li+1和Li的作用时间分别为tiH和tiL，满足

以上确定了合成参考相电压的两个电平及其作用时间，进一步可以确定各功率器件的开关状态。

3 仿真与实验研究

由文献［7］可知，对于多相集中整距绕组感应电机，当气隙磁密的基波分量与三次谐波分量的峰值之比为6、相位关系为“峰谷相对”时，其合成的波形最接近方波。在此条件下，定子磁链的基波与三次谐波的峰值之比为18，相位关系为“峰峰相对”。由此可得Te1/Te3≈36，据此即可确定k1=36/37和k3=1/37。

为验证理论分析，对一台额定功率为5.5 kW的五相集中整距绕组感应电机进行了仿真和试验，该电机额定运行时的电气及绕组参数如表2所示。

表2 五相感应电机参数Table 2 Parameters of five-phase induction motor

图6 电机空载定子反电势仿真与实验波形Fig．6 Simulated and experimental waveforms of back EMF of induction motor at no load

图6为采用不同控制方案下，电机空载、同步频率为50 Hz时，定子a相反电势的仿真与实验波形。从图中可以看出，实验结果与仿真结果相吻合。

图6（a）、（b）为方法1的仿真与实验波形，由于是空载运行，a相反电势与输入的相电压之间的误差较小;但随着负载的增大，两者之间的差距将明显增大。图6（c）、（d）为方法2的仿真与实验波形，由于基波和三次谐波磁链的相位关系受Δδ1和Δδ3影响较大，导致气隙磁密不符合控制要求，且磁密的最大值较大，额定运行时容易使磁场饱和。图6（e）、（f）为优化方法的仿真与实验波形，由于基波和三次谐波磁链间的相位关系不受任何参数影响，满足了电机气隙磁密的控制要求。

图7和图8分别为采用优化控制方案时，电机启动过程中的转速、转矩波形和额定工况时的相电流实验波形。实验结果表明，电机启动过程平稳，稳态相电流波动较小，满足控制要求。

图7 启动过程转速转矩实验波形Fig．7 Experimental waveforms of starting-up process

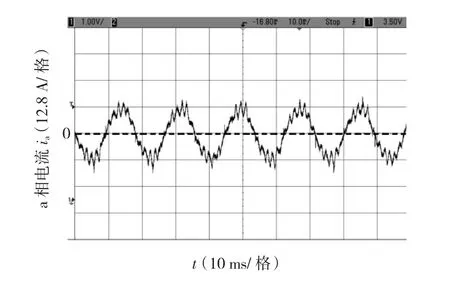
图8 额定工况时的相电流实验波形Fig．8 Experimental waveform of phase current under rated condition

4 结论

根据五相集中整距绕组感应电机的特点和控制要求，提出了3种实现三次谐波注入的五相感应电机的SVM-DTC方法，其中，方法1实现简单，但气隙磁密波形会随负载的变化而改变，不能完全满足控制要求。方法2对基波和三次谐波电压分别进行闭环控制，但由于磁链和转矩观测误差，造成磁链基波和三次谐波的相位关系不断变化，影响了控制性能。方法3——优化方法给定磁链三次谐波与基波之间的相位，在实现基波和三次谐波电压的闭环控制的同时，保证了磁链基波和三次谐波的幅值与相位的恒定，是可行的方案。仿真和实验结果验证了理论的正确性。

［1］DEPENBROCK M．Direct self-control（DSC）of inverter-fed induction machine［J］．IEEE Trans on Power Electronics，1988，3（4）:420－429．

［2］XU H S，TOLIYAT H A，PETERSEN L J．Five-phase induction motor drives with DSP-based control system［J］．IEEE Trans on Power Electronics，2002，17（4）:524 －533．

［3］TOLIYAT H A．Analysis and simulation of five-phase variable speed induction motor drives under asymmetrical connections［J］．IEEE Trans on Power Electronics，1998，13（4）:748－756．

［4］ 金爱娟，李航天，李少龙．五相异步电机的SVPWM控制技术［J］．电机与控制学报，2004，8（4）:377－381．

JIN Aijuan，LI Hangtian，LI Shaolong．SVPWM control of fivephase induction machine ［J］．Electric Machines and Control，2004，8（4）:377－381．

［5］ 张成胜，张晓锋，乔鸣忠，等．基于SVPWM五相感应电机直接转矩控制研究［J］．电机与控制学报，2008，5（12）:304－308．

ZHANG Chengsheng，ZHANG Xiaofeng，QIAO Mingzhong，et al．SVPWM method of five-phase induction motor direct torque control［J］．Electric Machines and Control，2008，5（12）:304 －308．

［6］SOSTHENSE F K．Dynamics and Control of a Five-phase Induction Motor［D］．Tennessee:Tennessee Technological University，2008．

［7］王东，吴新振，马伟明，等．非正弦供电十五相感应电机气隙磁势分析［J］．中国电机工程学报，2009，29（15）:88－94．

WANG Dong，WU Xinzheng，MA Weiming，et al．Air-gap MMF analysis of fifteen induction motor with non-sinusoidal supply［J］．Proceedings of the CSEE，2009，29（15）:88－94．

（编辑:张静）