空间网架结构整体工作性能的分析

袁 木炎,马乐为,张明文

(西安建筑科技大学土木工程学院,陕西西安710055)

空间网架结构下部多为混凝土框架结构、剪力墙结构或钢框架结构,而上部屋盖为钢网架结构。目前在设计计算此类结构时,我国由于结构设计软件功能的不足,通常将结构体系分为上下两部分独立进行建模计算,未考虑两部分结构的整体工作情况。实际上,由于钢结构和混凝土结构阻尼比不同,二者构成了非比例阻尼结构系统。上部钢网架除受直接作用的荷载外,下部体系的位移变形对其也有一定的影响,所以在计算分析过程中应考虑上下体系的整体工作性能。

本文采用有限元分析软件对该网架进行模态分析,验证结构整体建模与上部单独建模受整体稳定性和温度作用的不同结果,为类似网架结构设计提供依据。

1 工程概况

以某大学体育馆为研究模型,网架长70.6 m,宽57.6 m,顶标高22.6 m。下部采用钢筋混凝土框架结构,上部采用平板网架结构,节点采用螺栓球节点形式,场地为2类,抗震设防烈度为8度。

网架结构体系主要受力构件采用Q235B钢,其主要钢管规格为：Φ 60×3.5、Φ 75×4、Φ 88.5×4、Φ 114×4、Φ 140×4、Φ 159×6、Φ 159×8、Φ 159×10、Φ 180×8、Φ 219×8,工程结构模型如图1。

图1 某大学体育馆结构模型

2 有限元模型的建立

2.1 计算假定

网架结构的计算基本假定可归纳为：

⑴节点设为铰接,杆件只考虑轴向内力;

⑵依据小挠度计算理论进行计算;

⑶网架只承受节点荷载。

2.2 建立模型

该工程采用MIDAS/Gen软件建模分析,上部钢网架杆件以及下部结构中长细比较大的构件采用梁单元模拟,下部支承结构中的平面构件采用板单元模拟,得到单独的上部网架模型如图2所示,上下结构体系整体结构模型如图3所示。

图2 上部网架模型

图3 网架结构整体模型

3 稳定性对比分析

3.1 极限承载力对比

3.1.1 加载恒荷载

体系在网架跨中主节点竖向位移进行控制下进行恒荷载均布加载,分析单独上部结构模型和整体结构模型中上部网架的承载力变化,如图4所示。

⑴发展曲线在整体结构模型中控制位移在225 mm之前,随着控制位移的增加结构的承载力基本呈线性增长。控制位移超过225 mm后,结构的承载力迅速减小至零附近网架结构发生脆性失稳。随后,由于网架中杆件的应力表现为拉应力,随着控制位移继续增加承载力又缓慢增长,而在实际结构设计过程中控制位移超过225 mm时认为已经发生脆性破坏。

⑵控制位移达在225 mm之前,单独网架结构模型中结构的承载力呈线性增长。控制位移超过225 mm后,随着位移的增加结构的承载力呈现非线性缓慢增长。

⑶两模型承载力在结构极限承载力之前,单独网架结构模型比整体结构模型大8%～26%。超过结构极限承载力后,比值急剧增大3倍以上。所以在恒荷载作用下整体结构模型比单独网架结构模型设计安全。

3.1.2 加载活荷载

网架跨中主节点竖向位移进控制下加载均布活荷载,分析单独网架结构模型与整体结构模型中上部网架的承载力变化,如图5所示。

图4 恒荷载作用下分析模型的承载力发展曲线

图5 活荷载作用下分析模型的承载力发展曲线

⑴整体结构模型中,控制位移在225 mm之前结构的承载力线性增长。控制位移超过225mm后,随着其增加呈非线性缓慢增长,随后迅速下降。承载力由于网架中的类似薄膜应力的影响,在控制位移超过450 mm后而又稳步增长。

⑵单独网架结构模型中,结构的承载力在控制位移达到225mm之前同样线性增长。控制位移超过225 mm后,结构的承载力缓慢增长,随后迅速下降。结构的承载力在控制位移达到525 mm时稳步增长。

⑶均布活荷载作用下单独网架结构模型比网架整体结构模型承载力在达到极限承载力之前大7%～12%。结构屈服后,单独网架结构模型分析结果大。因而活荷载作用下若采用单独网架结构模型将使设计偏于不安全。

3.2 塑性铰分布对比

3.2.1 加载恒荷载

⑴接近极限承载力前整体结构模型第2、3、4位移子步对应的塑性铰分布如图6所示。

⑵达到极限承载力前,单独上部网架结构模型第2、3、4位移子步对应的塑性铰分布如图7所示。

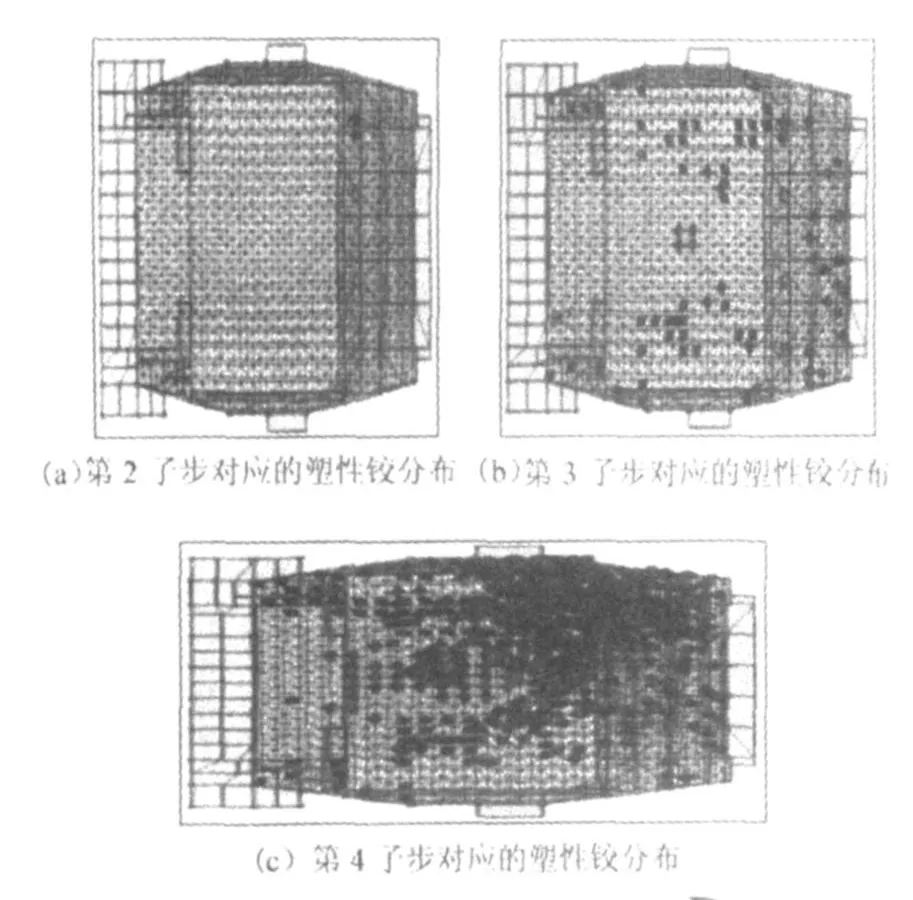
图6 恒荷载工况下网架整体结构模型的塑性铰分布

图7 恒荷载工况下单独网架结构模型的塑性铰分布

由上图示可得：①在均布恒荷载下,支座附近上弦杆首先达到屈服状态。随着控制位移继续增加,大部分上弦杆、腹杆和部分下弦杆屈服,整个上部网架接近极限破坏状态。②塑性铰在均布恒荷载下,在整体结构模型的分布比单独网架结构模型中较集中,说明上部杆件受下部支承结构的影响。

3.2.2 加载活荷载

⑴在活荷载加载下,接近极限承载力前整体结构模型第2、3、4位移子步对应的塑性铰分布如图8所示。

⑵接近极限承载力前单独上部网架模型第2、3、4位移子步对应的塑性铰分布如图9所示。由图8、图9可得：

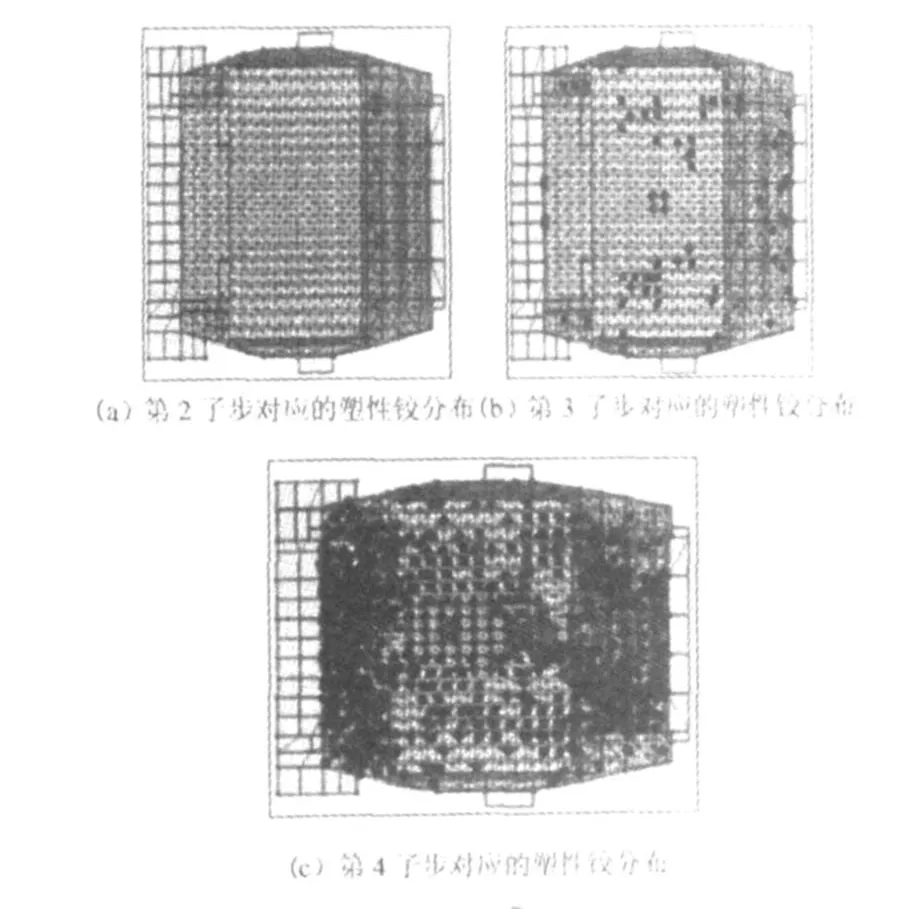
图8 活荷载工况下网架整体结构模型的塑性铰分布

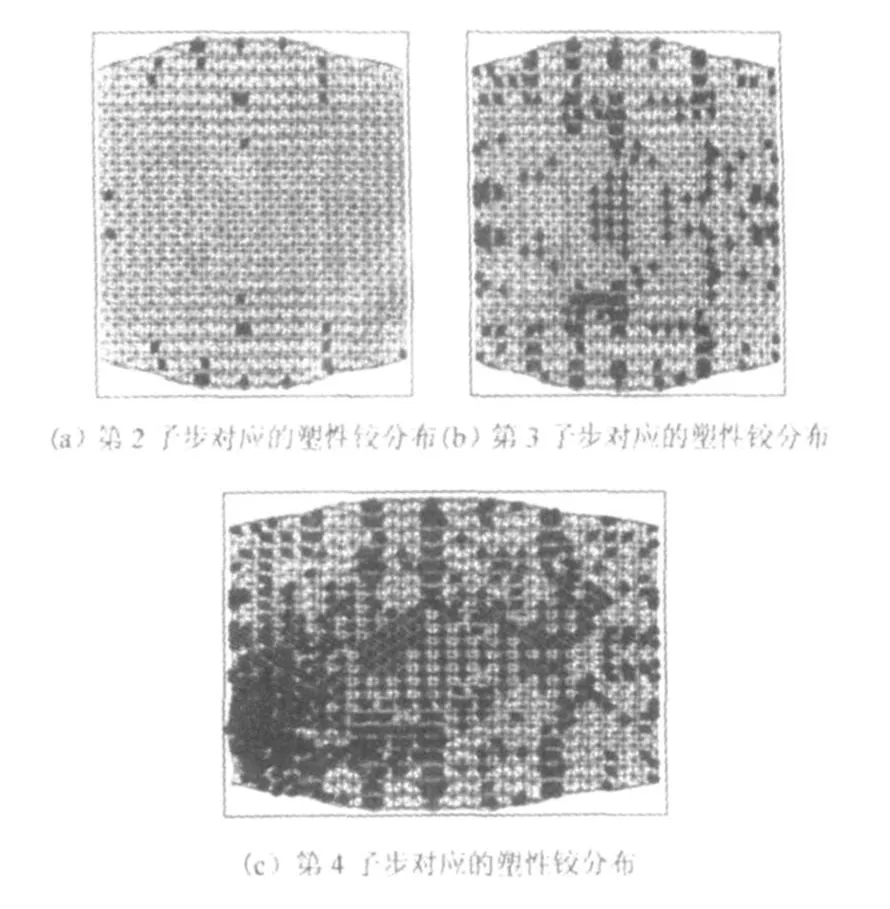
图9 活荷载工况下单独网架结构模型的塑性铰分布

4 温差作用影响下的对比分析

4.1 控制应力的选取

⑴网架支座轴线上弦杆轴向应力选取为：横向上弦杆由下到上依次分为23段;纵向上弦杆从左到右分为22段。

⑵网架支座节间上弦杆轴向应力提取为：横向上弦杆由下到上共有23段;纵向上弦杆从左到右共有22段。

⑶网架下弦杆轴向应力提取为：横向下弦杆由下到上共有22段依次编号;纵向上弦杆由左到右共有21段。

4.2 温差作用对网架杆件的影响

考虑工程所在地的实际气候特征以及该网架结构的保温隔热构造措施等影响因素,在分析过程中取30℃作为温差作用工况。

4.2.1 网架支座轴线上弦杆轴向应力

通过曲线的形式表示由整体结构分析和单独网架分析所得网架支座轴线上弦杆轴向应力数值,可得其在温差作用工况下的应力分布曲线,见图10和图11。

图10 支座轴线横向上弦杆应力分布

图11 支座轴线纵向上弦杆应力分布

由图10和图11可得：①单独网架分析模型计算的轴向应力两端大跨中小,并且应力值变化较大。②整体结构分析模型计算的轴向应力为：两端最大但数值大小远远小于杆件的屈服应力,而在跨中最小[11],同时从两端到跨中大部分应力数值在3MPa～30 MPa的正常范围之内变化较为平缓。③支座轴线横向上弦杆轴向应力采用单独网架分析比整体结构分析所得结果高10倍以上,纵向上弦杆轴向应力也相差3倍以上,说明单独网架模型夸大了温差作用的影响。

4.2.2 网架支座节间上弦杆轴向应力

由曲线的形式表示整体结构分析和单独网架分析两种方法所得网架支座节间上弦杆轴向应力数值,可得到温差作用工况下的应力分布曲线,见图12和图13。

图12 支座节间横向上弦杆应力分布

图13 支座节间纵向上弦杆应力分布

从图12、图13中可以看出：①单独网架分析模型计算的支座节间横向和纵向上弦杆轴向应力为：两端接近零,跨中较大。轴向应力总体较小,横向上弦杆轴向应力在25 MPa以内,而纵向上弦杆轴向应力在50 MPa以内。②整体结构分析模型计算轴向应力分布规律基本等同单独网架分析模型,横向上弦杆轴向应力维持在5 MPa以内,纵向上弦杆轴向应力维持在25 MPa以内,整个跨度范围内变化较为平缓,没有大幅度的应力突变情况。③单独网架分析所得结果比整体结构分析高,其中支座节间横向上弦杆大多数杆件的轴向应力数值高4倍以上,支座节间纵向上弦杆轴向应力在1.94～2.55倍,故上部网架单独建模分析夸大了温度对支座节间上弦杆的影响。

4.2.3 网架下弦杆轴向应力

曲线的形式表示采用整体结构模型和单独网架模型两种分析方法所得网架横向和纵向下弦杆轴向应力数值,可得温差作用工况下下弦杆轴向应力分布曲线,见图14和图15。

由图14、图15可得：①采用单独网架建模分析横向下弦杆应力数值在8MPa以内,纵向下弦杆的应力最大值在跨中。②整体结构分析横向下弦杆轴向应力数值维持在3 MPa以内,纵向下弦杆轴向应力数值维持在17.36 MPa以内。③单独网架分析比整体结构分析横向下弦杆大多数杆件轴向应力高1倍以上,纵向下弦杆多数杆件应力数值高40%以上。

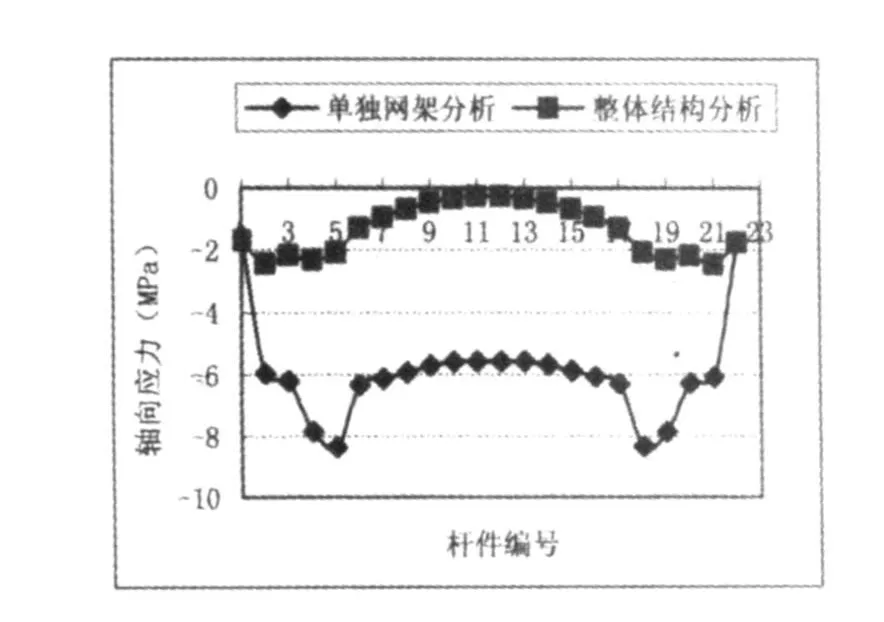
图14 横向下弦杆应力分布

图15 纵向下弦杆应力分布

5 结论

本文从整体稳定性、温差作用两方面对网架结构的整体结构模型和单独上部网架模型进行了对比分析,可以得出如下结论：

⑴网架竖向位移加载模式下,采用单独网架模型比整体结构模型分析所得稳定承载力数值大7%～26%,因而若采用单独网架结构模型将使设计偏于不安全,有必要考虑网架结构的整体工作性能。

⑵网架结构稳定性分析过程中,上部网架的杆件受下部支承结构的影响较大,建议在设计过程中对类似网架结构加强支座附近杆件的构造措施。

⑶温差作用下,单独上部网架分析模型夸大了网架杆件内力的温差作用,使杆件温度应力值偏大。

⑷两种分析模型在考虑温差作用下计算所得支座轴线上弦杆的轴向应力均为两端较大跨中较小分布状态,因此为防止上部网架因局部杆件屈曲而失稳破坏应适当加大网架支座附近上弦杆的截面面积,并加强与支承柱的连接。

[1] 刘大海,杨萃茹,钟锡根.空旷房屋抗震设计[M].北京：地震出版社,1989.

[2] Kenichi Kawaguchi.A Report on Large Roof Structures Damaged by the Great Hanshin-Awaji Earthquake[J].International Journal of Space Structures,1997(3)：135-147.

[3] 梁发强.非比例阻尼混凝土框剪及顶上钢塔结构弹性抗震分析[D].天津大学,2007.

[4] 程荣,殷志祥,李传增.网架结构损伤的数值模拟分析[C]//第七届全国现代结构工程学术研讨会论文集,2007.

[5] 张明文.空间网架与下部支承结构整体工作分析研究[D].西安建筑科技大学,2010.

[6] 刘文顺,苏德力,付明春,等.螺栓连接极限状态分析[J].平顶山工学院学报,2008,17(1)：62-64.

[7] 陈友泉.高强度螺栓连接的应用问题探讨[J].钢结构,2004,19(4)：23-25.

[8] 董石麟,钱若军.空间网格结构分析理论与计算方法[M].北京：中国建筑工业出版社,2000.

[9] 王昌兴.MIDAS/GEN实用实例教程及疑难解答[M].北京：中国建筑工业出版社,2009.

[10] 李青芳,李云.天津无缝钢管厂管加工车间网架设计[J].钢结构,1994,9(2)：88-93.

[11] 郑君华,黄呈伟.温差作用下空间网架的有限元计算[J].昆明理工大学学报,2002,28(6)：112-116.