中国人口增长中短期预测模型探讨

姚志鹏,陈盛双

(1华中师范大学汉口分校公共数学部,武汉430212;2武汉理工大学理学院,武汉430063)

人口问题是本世纪我国面临的最重大的问题之一.用数学建模的方法对人口发展的过程进行描述、分析和预测,进而研究控制人口增长和人口性别比例失调问题,早已引起各有关方面的极大关注,并成为系统科学、经济科学和人口科学应用研究中的重要交叉领域[1].

最早的人口预测模型是马尔萨斯模型.马尔萨斯模型的缺点在于没有考虑物种之间的竞争,自然界的平衡和人文环境因素.后来人们对马尔萨斯模型进行修正,提出了阻滞增长模型,此模型在一定时期内也取得了比较满意的结果.以上两种模型都是确定性的,只考虑了影响人口总数变化的时间因素.在此之后,人们又提出了考虑人口年龄分布状况的随机性模型[2].

由《中国人口统计年鉴》可得2001～2005年的城市、城镇和乡村的详细资料,包括各个区域的男性、女性的年龄人口分布、死亡率分布和生育率分布以及近10年来的整体性别比例和总体生育水平.本文就是从这些详细的资料中找出中国人口层次结构的特点,通过对现有特点的分析来建立适合我国的中短期模型.

1 基本假设

(1)假设数据是基本准确可靠的,不存在巨大偏差和误报;

(2)假定我国在近期的死亡率、生育率和性别比例是按目前发展趋势变化的,不会出现巨大的意外(重大灾害、政策等)造成大幅度数据变动;

(3)在中短期预测中,不考虑老龄化的急剧增加和计划生育政策的变动;

(4)不考虑生存空间等自然资源制约,也不考虑意外灾难、战争等非可抗力因素对人口数量的影响.

2 简单模型的建立

2.1 问题的引入

根据近年人口调查的相关数据和关于人口战略的研究报告,建立数学模型来预测中国未来的人口增长趋势.对于该问题我们着重从影响人口发展的死亡率、生育率以及性别比3个主要因素进行分析.

对于本问题,首先在一个完全理想的环境中进行分析并建立简单模型.假设1:在某个封闭的环境下,人口没有迁入或迁出情况;假设2:所有的统计数据都是正确的,不存在测量误差;假设3:整个模型的人口演变只由生育、老化和死亡引起,没有其他意外因素.

通过考虑n年i岁的人口数量F(n,i)、死亡率B(n,i)、新生人口数量N(n),得到n+1年i+1岁的人口数量为:

其含义是:n+1年的0岁人口数量是n年新出生的人口、i+1岁的人口数量是n年i岁人口中存活的数量,其中90岁以上的人口数量是n年中89岁和90岁以上的人口中存活的数量.

2.2 简单模型的建立

假设时间以年为单位,年龄按周岁来计算,记M i(t)为t年i岁的男性人口数量,W i(t)为t年i岁的女性人口数量,i=0,1,2,…,90.有

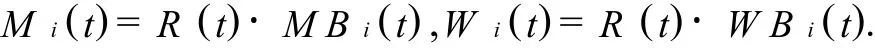
其中:R(t)为t年的总人口数量,M B i(t)为t年i岁男性的比例,W B i(t)为t年i岁女性的比例.

BM i(t)为t年i岁男性人口的死亡率,BW i(t)为t年i岁女性人口的死亡率,即:

于是,M i+1(t+1)=(1-BM i(t))M i(t),

记hi(t)为t年i岁女性生育率,根据统计数据,i=[15,49]为育龄区间,则t+1年新增人口(0岁人口)为:设S(t)为t年新出生人口的男女比例,则t年新生小孩中男性人口数为:

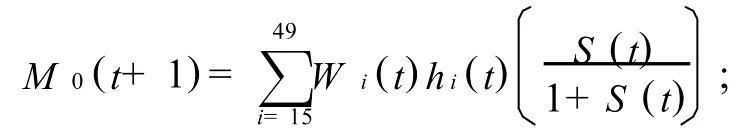
t年新生小孩中女性人口数为:

当i=89时,有:

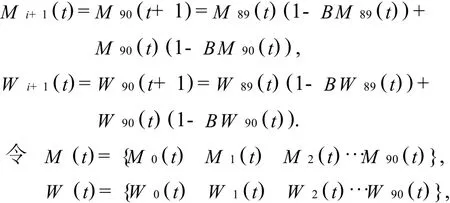
则t+1年男性总数量为:

其中,矩阵A(t)是由t年各个年龄层的男性存活率构成,矩阵B(t)由15～49岁间女性生育率构成:

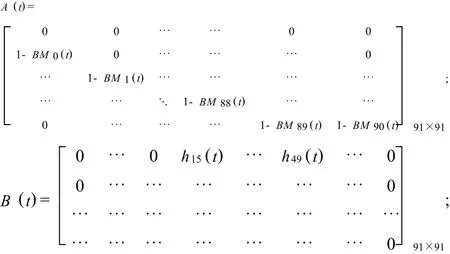
同理t+1年女性总数量为:

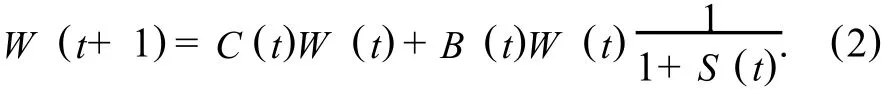
矩阵C(t)是由t年各个年龄层的女性存活率构成,C(t)=

式(1)和(2)的一阶差分方程就是人口预测的基本数学模型.其中A(t)和C(t)是依赖每年死亡率的矩阵,B(t)是依赖每年生育率的矩阵.

利用此简单模型,将相关数据代入进行计算,将城市、城镇和乡村作为3个独立的系统分别考虑,计算出各个系统的总人口数量,最后相加得到我国的总人口数量.

根据官方提供的我国人口资料,可查得2001～2006年的中国总人口数.通过M atlab利用第n年的数据来预测第n+1年的总人口数(见表1).

根据得到的数据,发现预测数据和实际数据存在出入,这表示此简单模型还无法精确地预测我国的人口,还需要对此模型进行进一步优化,得到更精确的模型.

3 中短期预测模型的建立

3.1 中短期模型的基本问题

中短期预测和长期预测不同,中短期预测可以根据前一年的数据来预测未来几年的数据.中短期预测的特点是未来的发展基本遵循当前的增长规律,不会出现太大的数据变动.

要建立预测模型,首先要确定第2部分中提及的A(t)、B(t)、C(t)矩阵,而这3 个矩阵,是依赖于生育率和死亡率的.

每年的总体生育水平是会发生变化的,这受到政策、经济状况等方面的影响,分析2001～2005年的数据发现,虽然整体生育水平不同,但在一年中各个年龄的生育率是遵从一定规律的.

3.2 每年总体生育率和死亡率的预测模型

总体生育率和总体死亡率是反映在一年中整个区域内的人口生育比率和死亡比率,这受许多因素影响,无法根据所给的资料进行计算.

灰色预测模型GM(1,1)是单变量一阶线性模型[3],它是灰色预测模型中最基本的模型.它比多变量多阶预测模型或其他模型计算简单,预测效果较好,且兼有对样本容量和概率分布无严格要求的特点.该模型广泛应用于不可知因素的预测.

本文对总体生育率、总体死亡率和出生男女比例的预测均采用灰色预测模型,此模型GM(1,1)对于短期无规则数据预测效果较好,但不适用于长期预测.

灰色预测模型的基本原理和计算方法详见文[4].

利用M atlab对灰色预测模型GM(1,1)进行编程[5],由《中国人口统计年鉴》(2001～2006)的生育率、死亡率和新生男女比例录入到程序中,预测出未来几年的生育率(见表2)、死亡率(见表3)和男女比例(见表4).

表2 2006～2010年总体生育率的预测Tab.2 2006～2010 to tal fertility rate p red iction %

表3 2006～2010年男女死亡率的预测Tab.3 2006～2010m en andw om en death rate p red iction %

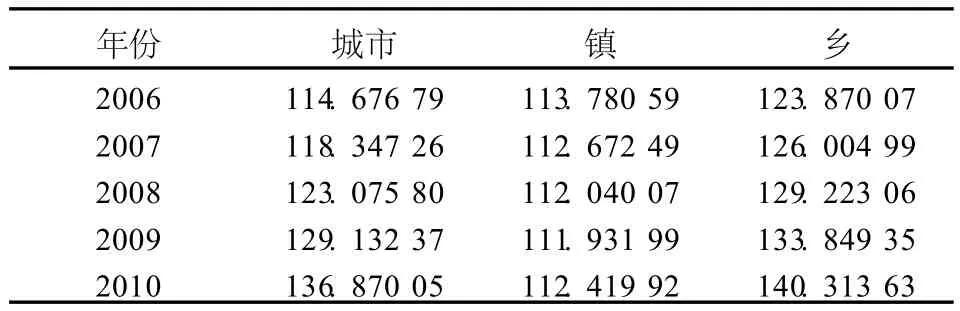
表4 2006～2010年男女比例的预测Tab.4 2006～2010m en and w om en p ropo rtion p red iction

3.3 分年龄生育率模型

分年龄生育率可以描述不同年龄妇女的生育力差别,是分析人口年龄结构变化趋势的重要数据[5].妇女生育率随年龄变化的趋势接近于正态分布,其数学形式可以描述为:

其中i为妇女生育年龄,f(i)为生育率,h(i)为特定的随机分布,k为尺度变换因子,与总体生育水平有关.

基于对数正态分布的分年龄生育率模型为:

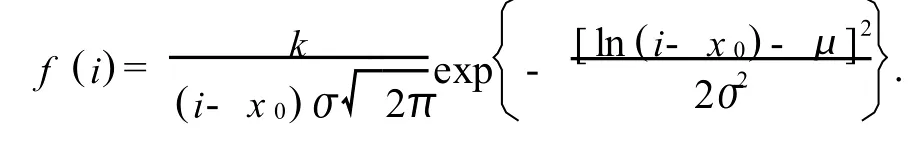
式中x0为起始生育年龄,根据本文数据,令x0=15;k为对数正态分布函数所对应的尺度变换因子.

泊松分布近似于正态分布,基于泊松分布的分年龄生育率模型为:

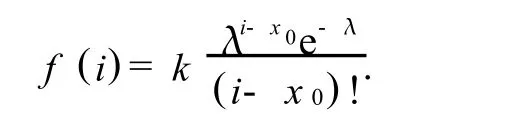
式中:起始生育年龄x0也取15岁,k为泊松分布函数所对应的尺度变换因子;λ是决定因素,表示从起始年龄x0到平均生育年龄的时间长度.

综合正态分布和泊松分布,得到组合的分年龄生育率模型:

其中参数μ,σ,λ与对数正态分布、泊松分布模型中的参数相同,α为权值,k为尺度变换因子,即总体生育率.

将2001～2005年的数据作为统计值进行检验,以此5年的误差值作为目标函数,使其最小:

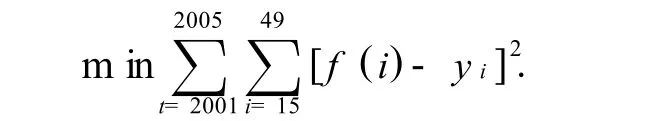
需要说明的是,每年的k是随每年的总体生育率而变化的,yi为实际生育率.

表5是根据5年的数据估计出来的参数,因篇幅原因,每年通过函数计算得到的生育率不在此列出,将2005年的生育率和函数计算得到的生育率拟合可得图1.

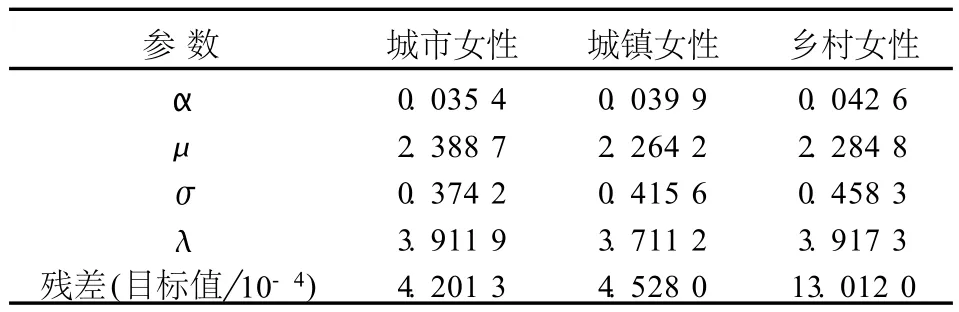
表5 生育率分布模型参数Tab.5 Fertility d istributionm odelparam eter

图1 2005年的实际分年龄生育率和函数计算得到的分年龄生育率比较图Fig.1 Com pare g raph o f the actua l and the calcu lative fertility rate o f each age

由图1和残差数据可以看出,估计的参数基本满足条件,因此,假设第t年城市生育率为k,则t年i岁的生育率为:

其中α、μ、σ和λ为表5中所估计出来的参数值.

3.4 分年龄死亡率模型

死亡率根据年龄的分布也是服从一定规律的,除0岁的新生儿因其他非可抗力的影响死亡率偏大外,其他年龄的死亡率服从一定规律.分析数据后可知,随着年龄的增长,死亡率逐渐增大.

本文对分年龄死亡率模型使用如下函数:

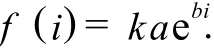
其中k为该年的总死亡率,a和b是此函数的参数,表示死亡率随年龄增长的趋势和年龄的死亡率参数.

只选取1～90岁进行分析,定义目标函数:

它表示5年内的死亡率误差的平方和,求解参数a和b,使总误差最小.yi为实际死亡率.

表6是根据5年数据估计出来的参数,以及利用函数计算得到的死亡率分布.

表6 死亡率分布模型参数Tab.6 Death d istributionm odelparam eter

3.5 预测模型求解

根据上面的求解,已经能够将ht(i),BM i(t),BW i(t)以及S(t)求出,因此可以预测对应的A(t),B(t),C(t),然后代入(1)式和(2)式中,即可预测今后几年的人口结构和年龄分布.

表7为根据预测模型预测的2006～2010年人口总体预测结果(人口年龄和死亡率结构及生育率结构数据略).

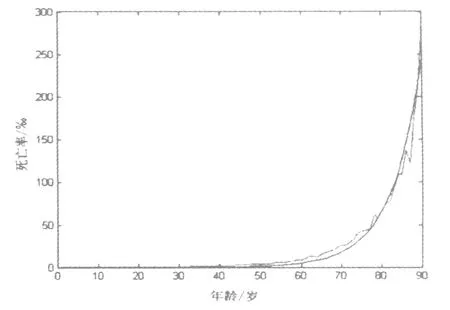
图2 2005年拟合图与实际死亡率的比较图Fig.2 Fitting g raph of the actualand the calcu lative death rate o f each age

因篇幅原因,每年通过函数计算得到的死亡率不在此列出,将2005年的死亡率和函数计算得到的死亡率拟合如图2所示.

由图2和残差数据可以看出,估计的参数基本满足条件,因此,假设第t年城市男性死亡率为k,则t年i岁的男性死亡率为BM t(i)=kaebi.其中a和b为表6中所估计出来的参数值.

表7 2006～2010年人口总体预测结果Tab.7 2006～ 2010 to talpopu lation p redictive resu lt 104 人

4 结果与优缺点分析

本文在模型设计时,考虑了大部分因素,以求预测结果的精确性.

在中短期预测中,主要是利用拟合方法来对生育率和死亡率的年龄分布进行预测,且拟合效果都比较理想.利用灰色预测理论对未来几年的总体生育率、死亡率和性别比例进行预测,是在大量条件未知的情况下最理想的预测方法.

本文所建立的模型,对生育率和死亡率进行了准确的拟合和预测,并对未来几年的人口年龄层次进行了详细的预测,使人们对未来的人口结构有更清晰的认识.

本文的中短期预测模型建立在递归基础上的,具有数据可靠、推算精确等特点,而灰色预测理论和拟合方法,更是提高了预测数据的精确性.

但本文建立的模型由于各个方面的影响,仍然有许多不足,特别是在中短期模型上,没有考虑到城市、城镇和乡村之间的人口迁移和结构变化,以及人口老龄化(年龄结构分布的变化)以及生育年龄推迟(正态分布的曲线右移)等因素,这些因素将在以后的研究中详细考虑.

[1] 蒋正华.人口分析与规划[M].西安:陕西科学出版社,1984.

[2] 宋 健.人口预测和控制[M].北京:人民出版社,1980.

[3] 邓聚龙.灰色系统基本方法[M].武汉:华中理工大学出版社,1987.

[4] 赫永红.灰色动态模型及其在人口预测中的应用[J].数学的实践与认识,2002(9):74-79.

[5] 李勇胜.人口预测中的模型选择与参数认定[J].财经科学,2004(2):68-72.