基于燃气射流控制的可调进气道数学模型研究①

冯喜平,林志远,郑 亚,单建胜

(1.西北工业大学燃烧、流动与热结构国家级重点实验室,西安 710072;2.中国航天科技集团公司四院四十七所,西安 710025)

0 引言

固冲发动机的固有优点使其成为战术导弹的理想动力装置。导弹在机动飞行过程中,飞行状态发生变化,通过进气道进入燃烧室的空气流量和流动参量也相应发生变化,随之二次燃烧偏离理想状态,燃烧效率会降低。为保证二次燃烧条件不过大偏离理想状态,需进行一次燃气或冲压空气的调节。由于一次燃气流量调节存在一定困难,进气道调节有可能成为提高燃烧效率的途径。

可调进气道研究工作可分为机械式调节方案、磁控进气道方案、附面层控制技术及二次流体控制方案等[1-7]。其中,二次流体控制方案具有调节结构简单、所需几何空间小等优点,有望成为固冲发动机进气道调节的理想方案。

建立可调进气道数学模型对可调进气道研究具有重要的指导意义。国内对进气道的数学模型进行了一些研究工作,卢燕等[8]以数值模拟结果为基础,归纳出进气道主要性能参数、状态参数和几何调节参数之间的关系,建立了二元超声速进气道的数学模型。利用此数学模型,可确定进气道在不同状态下的性能参数。时瑞军等[9]以数值仿真结果为基础,利用B样条理论建立了反映攻角、马赫数及可调斜板角度变化的超声速进气道数学模型。这些数学模型大多针对进气道斜板角度可调建立的,反应的是机械式可调进气道的性能参数。

继前期研究工作[10],文中以燃气射流控制可调超声速进气道为研究对象,对其内流场进行数值模拟,并以流场计算结果为基础,归纳出进气道性能参数与状态参数和射流喷射条件之间的关系,从而建立燃气射流控制可调进气道的数学模型。利用此数学模型,可确定进气道的综合性能随射流喷射条件的变化关系,作为燃气射流控制系统研究的基础。

1 燃气射流控制可调进气道方案

固冲发动机由于几何空间限制,一般采用不可调进气道。定几何进气道在非设计状态下性能品质会降低。针对此问题,文献[10]提出了一种射流控制可调进气道方案。首先,在进气道设计时选择了较低马赫数封口的方案,进气道工作时其调节过程为当工作马赫数低于封口马赫数时不进行调节;当工作马赫数高于封口马赫数时,从固冲发动机补燃室(或燃气发生器)引入一股气流,通过管路输送到进气道各级压缩面和喉道附近,再通过布置于压缩面和喉道下壁面的多孔板(孔设计成小型喷管)将气流加速后喷入。

图1为进气道调节机理示意图。文中对调节机理进行了进一步研究。进气道调节机理基于喷射射流对激波的干扰原理,借助射流去影响主流状态,使其改变方向:

(1)进气道第1、第2道压缩波调节机理建立于向超音速主气流中喷入二次气流时,二次喷流对主流流场作用原理。

当进气道工作于超额定状态时,在进气道压缩斜面前部喷入第二股气流,这股气流迅速膨胀,并转折附面流动,对超音速来流形成障碍,其流动情况相当于超音速气流绕钝头问题的流动,超音速气流受喷射气流的干扰在喷射点上游形成一系列激波,与进气道斜压缩波交汇并相互作用,使得压缩波产生弯曲。

在适当位置布置喷流孔,并调节二次流参数,可改变二次流所形成激波的强度和角度,这样二次流形成的激波和进气道压缩波的相互作用会发生变化,主流偏斜随之改变,压缩波角度也会发生变化。射流的喷入使主流转折角增大,斜激波向外偏折,最终保持在封口附近,这样就实现了对进气道口部波系的控制。

二次射流和主流之间的相互作用非常复杂。2股气流会发生混合、进行热和动量的交换,主流气流的温度、压力和速度场都会发生变化。

(2)喉道面积的调节机理也是基于射流对流场的干扰原理。注入射流后,使主流气动边界向外偏折,进而控制有效喉道面积。改变喷射条件就可实现有效喉道面积的调节,进而减小喉道出口马赫数。

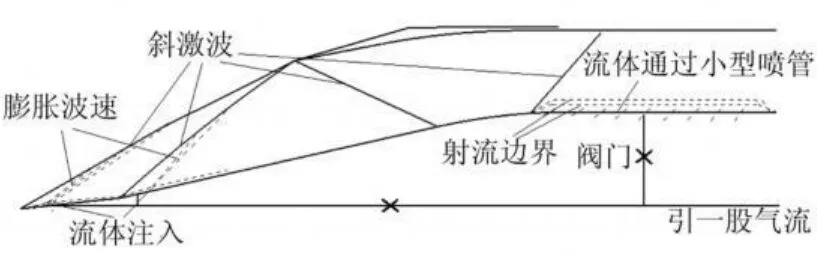
图1 射流控制可调进气道示意图Fig.1 Jet controll inlet

2 可调进气道物理模型及流场数值计算方法

2.1 物理模型

(1)冲压发动机工作要求飞行高度10 km;设计点Ma=2.5;设计状态无溢流,流量3 kg/s;起动Ma=2.2;最大飞行Ma=3.5。根据总体性能要求确定进气道长1 080 mm,高98mm;高宽比1∶1。

(2)采用三斜一正四波系结构,外压缩部分压缩角分别为6°、7°,外罩内壁面和水平线夹角8°,内收缩比1.16。选取大半径弯曲唇口构形,采用等截面积直喉道段,喉道之后采用等面积比扩压,扩张角5°。基本结构如图2所示。

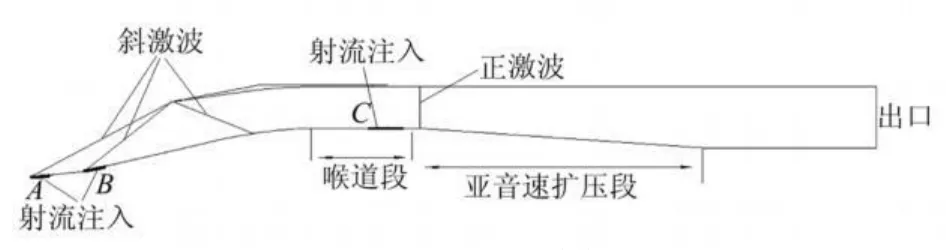
图2 进气道结构简图Fig.2 Con figuration o f the inlet

(3)调节时A、B、C处是射流注入区;A处布置10个射流入口,B处8个,宽度均为1 mm,入口间隔1 mm;C处布置10个宽度2 mm入口,入口间隔4 mm。

2.2 数值计算方法

控制方程选用二维定常的雷诺时均Navier-Stokes方程,湍流模型采用RNG k-ε湍流模型,采用基于Simple算法的有限体积法求解进气道流场。近壁面区域采用壁面函数法处理。

计算网格为结构化网格,在壁面附近进行了网格加密(图3)。计算中,将NM、LK和JI处布置的小孔简化为入口边界以供应射流,简化射流为热空气。采用的边界条件如下:

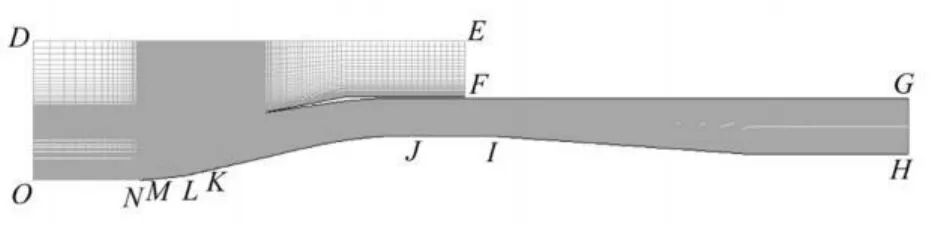
图3 计算域网格Fig.3 Grids of calculation domain

(1)OD、DE为压力远场边界,NM、LK和JI处布置的射流入口简化为压力入口边界;

(2)EF、GH为压力出口边界,EF设置反压为零;

(3)ON为绝热滑移壁面,进气道壁面选择绝热无滑移壁面条件。

3 可调进气道数学模型的建立

可调进气道数学模型是燃气射流控制技术研究的基础。准确可靠的数学模型,可快速预估进气道性能参数,可方便进行进气道影响因素分析,从而大大减小可调进气道设计时间,并提高工作效率。

样条函数具有用低阶项较好逼近各种非线性的特点,且生成曲线(曲面)具有较高的光滑度,在非线性问题的研究中得到广泛应用。B样条具有计算稳定、快速的特点,是目前应用较广的曲线/曲面拟合方法。文中采用B样条最小二乘曲面拟合方法,建立燃气射流控制可调进气道数学模型。

3.1 B样条最小二乘曲面拟合方法[9]

B样条曲面表达式为

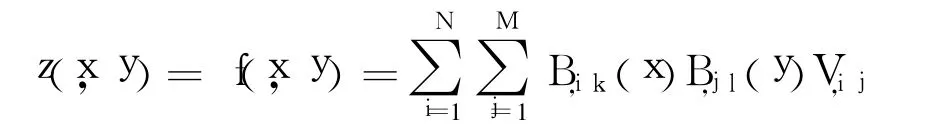
B样条最小二乘曲面拟合的思想是设曲面F(x,y)在网格点(xu,yv)上的函数值已知。其中,u=0,1,…,n-1,v=0,1,…,m-1。用最小二乘法求逼近参数使得f(x,y)与F(x,y)在网格点(xu,yv)上误差的平方和最小,即

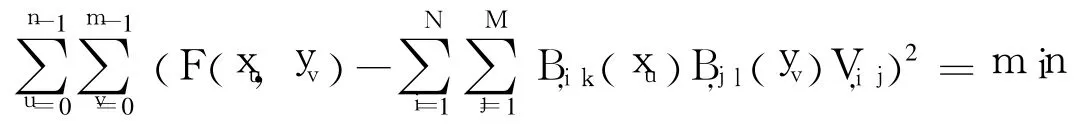
3.2 燃气射流控制可调进气道数学模型

射流控制进气道基于定几何进气道,通过射流干扰流场而实现进气控制,影响进气道主要因素是射流特性(射流物性、入射位置和入射点分布、流量和入射角等),选择入射角和入射流量为控制参数,进气道特性关系可表示为

式中 l1表示第1道斜激波和唇口距离;l2表示第2道斜激波和唇口距离;σ表示进气道出口总压恢复系数;φ1、ϑ1分别表示第1级斜板喷射的射流流量和射流入射角;φ2、ϑ2表示第2级斜板喷射的射流流量和射流入射角;φ3、ϑ3表示喉道喷射的射流流量和射流入射角。

根据进气道流场数值模拟结果,利用B样条曲面拟合建立燃气射流控制可调进气道数学模型。第1道斜激波拟合条件:射流入射角15°、17°、19°,马赫数2.6、2.7、2.8、2.9、3.0共5个点,射流流量0.000、0.006、0.014、0.028、0.041、0.050、0.069 kg/s。根据以上拟合理论,得到第1级压缩面射流入射角15°时,系数矩阵:

射流入射角17°时,系数矩阵:

射流入射角19°时,系数矩阵:

第2道斜激波的函数关系和第1道斜激波相似。在第1道斜激波已经调节封口的条件下,数值计算了(第2级压缩面射流入射角21°,来流马赫数分别为2.6、2.7、2.8、2.9、3.0,第2级压缩面射流流量分别为0、0.001 72、0.006、0.011、0.02、0.030、0.042、0.048 kg/s时)第2道斜激波距唇口位置和来流马赫数的流场,得到系数矩阵:

喉部调节拟合条件:喉道射流入射角8°,来流马赫数2.6、2.7、2.8、2.9、3.0,喉道射流流量0、0.080 14、0.105 9、0.125 9、0.144 7、0.161 4 kg/s,拟合后的系数矩阵:

3.3 射流控制可调进气道数学模型分析

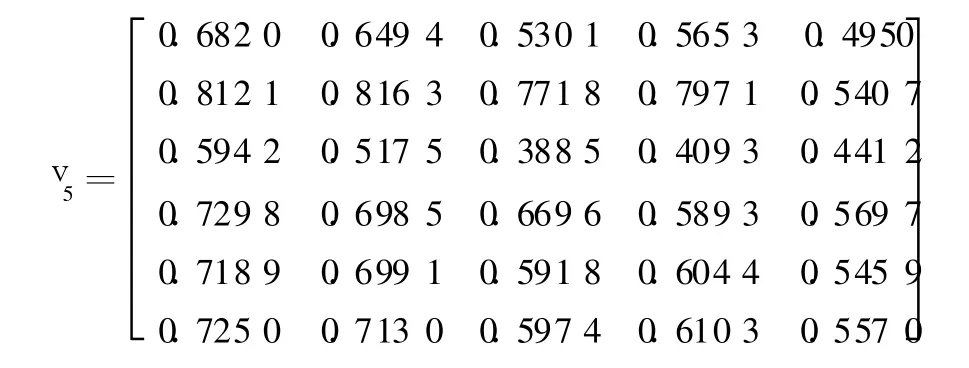
由图4可见,随着射流流量增加,第1道斜激波距唇口位置随射流流量呈减小趋势。这是因为射流流量增大时,射流喷射动量增加,射流穿透深度增加,射流和主流形成的“接触面”和第1道压缩面夹角增大,主流经过的压缩角增大。因此,激波角也相应增大,斜激波向靠近唇口移动。

图4 不同入射角条件下Ma、射流流量和第1道激波位置三维函数关系Fig.4 3D functional relation of M a,jetmass rate with position of the first shock at different jet angle

随着射流入射角的增大,射流水平方向速度减小,垂直方向速度增加,垂直方向喷射动量增大,射流在垂直方向的影响区域相应增大。因此,对主气流的阻碍作用增大,射流和主流相互作用形成的“接触面”和水平方向夹角增大,主流进过的压缩角增加,斜激波向外偏折,向靠近唇口移动。

图5为第1道斜激波调节封口条件下第2道斜激波的调节规律,其变化趋势与第1道斜激波相同。

图6表示喉道注入射流后进气道总压恢复随射流流量的变化曲面。可看出,随着射流流量的增加,进气道总压恢复呈增大趋势。

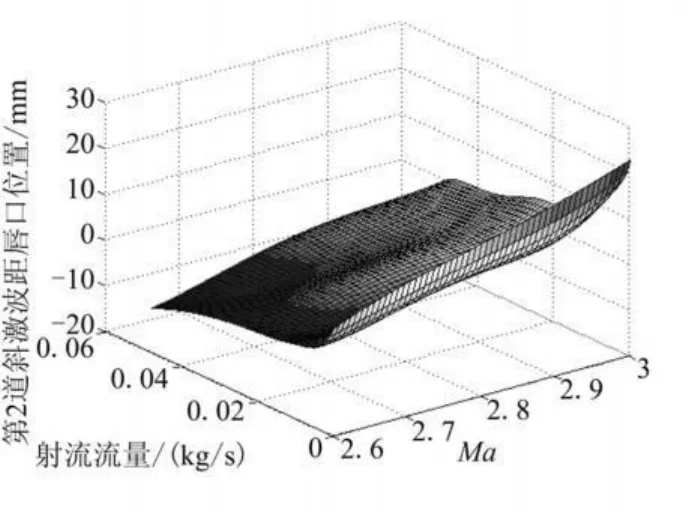
图5 第1道斜激波调节封口条件下Ma、射流流量和第2道激波位置三维函数关系Fig.5 3D functional relation o f Ma,jetm ass rate with position of the second shock at condition of the first shock on lip

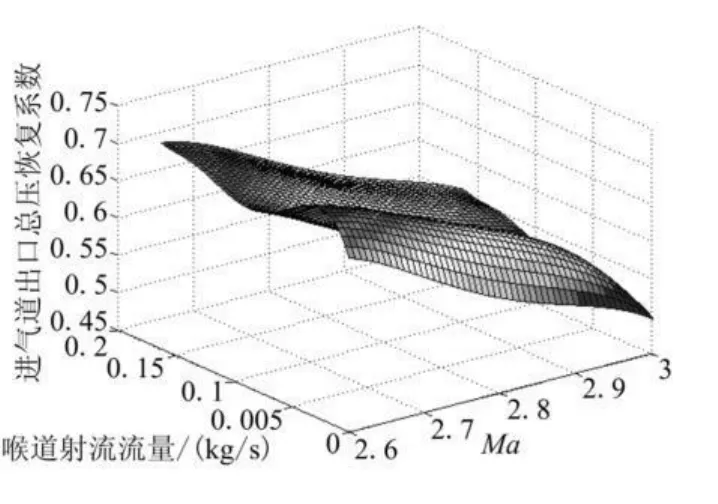
图6 喉道射流入射角8°条件下Ma、喉道射流流量和进气道出口总压恢复系数三维函数关系Fig.6 3D functional relation of Ma,jetm ass rate of throat with TPR at condition of 8°throat jet angle

为验证该数学模型的准确性,对比了一系列马赫数工况下流场模拟结果和数学模型计算结果。如在工作Ma=2.75工况下,流场计算结果和数学模型计算结果对比如下:在第1级压缩面射流入射角17°条件下,第1道斜激波调节封口所需射流流量流场计算结果为0.021 0 kg/s,数学模型计算结果为0.021 6 kg/s,相对误差为3%;第2道斜激波调节封口所需射流流量为0.009 1 kg/s,数学模型计算结果为0.008 8 kg/s,相对误差为3.3%;喉道射流入射角8°,射流流量0.161 7 kg/s,总压恢复系数流场计算结果为0.645,数学模型计算结果为0.651,相对误差为0.9%。计算发现,该燃气射流控制可调进气道数学模型拟合精度较高,与数值模拟结果误差较小。

4 结论

(1)针对燃气射流进气道调节方案,以飞行马赫数变化时不同流量和入射角的流场计算结果为基础,采用B样条最小二乘理论,建立了燃气射流控制可调进气道数学模型。由模型可看出,当进气道工作在超额定状态时,增大射流喷射角和喷射量,外部斜激波激波角增大,进气道出口总压恢复系数也有增加趋势。

(2)该模型可计算出当进气道工作于超额定状态时,调节外部波系封口所需射流条件随飞行马赫数的变化规律,并可计算出飞行马赫数变化时进气道出口总压恢复系数随喉道射流喷射条件的变化规律。因此,可作为燃气射流进气道调节系统设计的基础。

[1] Ryan P.Off-design performance characterization ofa variable geometry scramjet[R].AIAA 2005-3711.

[2] Yusuke M.Multi-row disk arrangement concept for spike of axisymmetric air inlet[R].AIAA 2004-3407.

[3] Macheret SO,Mikhail N S,Richard BM.Magnetohydrodynam ic control of hypersonic flows and scram jet inlets using electron beam ionization[J].AIAA Journal,2002,40(1):74-81.

[4] Bobashev S V,Erofeev A V,Lapushkina T A.Recent results on MHD flow control at Ioffe institute[R].AIAA 2006-8012.

[5] David D Young,Stewart A Jenkins and Daniel N Miller.A investigation of active flow field contol for in let shock/boundary layer interaction[R].AIAA 2005-4020.

[6] Richard G Haws,Jeff SNoall,Russell L Daines.Computational investigation ofa method to compress air fluidically in supersonic inlets[J].Journal of Spacecraft and Rockets,2001,38(1):51-59.

[7] 谭慧俊,陈智,李光胜.基于激波控制的定几何高超声速可调进气道概念及初步验证[J].中国科学E辑,2007,37(11):1469-1479.

[8] 卢燕,樊思齐,马会民,等.超声速进气道数学模型研究[J].推进技术,2002,23(6):468-471.

[9] 时瑞军,卢贤锋,樊思齐.超音速进气道建模方法研究[J].航空动力学报,2004,19(4):466-471.

[10] 冯喜平,林志远,郑亚,等.固冲发动机射流控制可调进气道研究[J].固体火箭技术,2010,33(4):396-400.