应用6σ质量控制方法的空射巡航导弹概念设计①

马 英,何麟书,邓家褆

(1.北京航空航天大学机械工程及自动化学院,北京 100191;2.北京航空航天大学宇航学院,北京 100191)

0 引言

在现代产品概念设计阶段,多学科设计优化方法(Multidisciplinary Design Optimization-MDO)被广泛用以确定设计参数。由实际经验可知,确定性最优化的结果经常处于可行域的边界上,这种设计方法并未考虑设计参数的波动。实际上,导弹在储藏、转运、温度变化、湿度变化和震动等因素会引起装药参数、舵面形状等偏离最优设计结果,从而引起设计失效,因此,通过确定性优化方法得到的最优方案并不意味着在实际工程中可行。为了解决这一问题,还需要找到系统的稳健解,即对设计参数波动非常“迟钝”的解。找到这样解的过程就是稳健性设计(Robust Design-RD)过程。RD将产品质量控制融合至产品设计阶段,是实现现代工业产品质量控制的重要手段之一。对于空射巡航导弹而言,为了确保产品质量,就不能只停留在寻求最优性能方案上。

文中将一种现代质量控制方法,即面向6σ的稳健性优化方法用于空射巡航导弹的概念设计中,目的是找到一种对设计参数波动具有较强抗干扰能力的总体方案。

1 质量控制方法概述

1.1 传统稳健性设计方法及其应用难点

传统稳健性设计方法的代表为田口方法,其特色之一是将系统质量衡量标准转换为信噪比函数。田口方法为质量控制提供了一个强有力的工具,它改变了过去只能通过对产品做实验进行质量控制的被动方法,将质量控制直接结合到产品设计中,是产品质量控制领域的一大进步。传统的田口方法在应用中也遇到了一些困难,总的来说有以下几点:

(1)信噪比函数的有效性是有条件的,那些影响系统均值的控制因素和影响系统性能方差的因素必须互不干扰、相互独立。信噪比能作为有效的系统质量衡量标准的前提是用于调整系统均值的尺度系数必须存在,而且质量指标的均值和方差成比例变化[1]。这样的条件是十分苛刻的,因为真实系统中影响这二者的因素往往无法实现这种分离。

(2)传统的田口方法需要的试验次数较大,一般至少为Nin×Nout,其中Nin和Nout分别代表内设计试验次数和外设计试验次数。

(3)田口方法会遇到著名的“维数灾难”瓶颈[2],对1个n维2水平的设计向量而言,需进行的分析次数会达到2n次,这往往造成计算量增长过快,也正是这个特点,决定了田口方法是将稳健设计的设计变量定义在离散空间上,很难处理大范围设计变量。

(4)田口方法不能直接处理有约束问题,必须采取相应措施,例如定义罚函数,将有约束问题转换为无约束问题处理[1]。

1.2 面向6σ的产品质量控制

为了解决上述传统质量控制方法的缺点,研究人员想到了将稳健性设计问题与优化问题相结合的方法,从而产生了稳健性优化(Robust Optimization-RO)。RO的优点包括可直接处理连续设计空间、直接处理设计约束和综合考虑各控制因素、噪声因素对设计目标均值和方差的影响。文中采用的面向6σ的质量控制方法就属于这种类型的稳健性优化方法。

传统认为,系统性能和约束对设计变量波动的敏感性达到3σ保证可行的水平,就已足够稳健了。航空航天领域对稳健性[3]的表述为稳健系统被设计和验证为有承受参数波动3σ的能力,并具有操作费用、可靠性、维修性和性能的最佳组合。

然而,文献[4]表明,在3σ质量水平下,产品长期百万次失效率将达到66 803次,而在6σ质量水平下,该值为3.4。因此,3σ水平在现代质量管理中仍被认为是不够的,6σ质量控制的思想逐渐扩展到了整个工程设计领域。文献[5]就是一个在航空航天领域的产品设计中应用6σ质量管理的例子。

2 空射巡航导弹稳健性设计实施过程

2.1 导弹多学科模型的建立

文中研究的空射巡航导弹采用常规圆柱体气动布局,X型舵面。多学科模型分为结构外形、动力、质量、气动和弹道5个子学科,每个学科采用相应的建模工具建立分析模型。其中,结构、质量和动力学科采用CAD三维建模软件进行参数化建模,计算导弹和发动机的外形尺寸、质心、转动惯量等特性参数。结构学科部件划分如图1所示。

图1 结构学科部件示意图Fig.1 Com ponents of them issile

气动学科采用气动分析软件进行分析,基本原理为将弹体划分为基本部件,根据工程经验公式分别计算各部件启动特性,从而得到整体气动特性,计算出各种气动系数及其导数。

动力学科则负责根据燃料特性等发动机设计参数,计算发动机推力、工作时间等性能参数。

弹道学科采用simulink工具进行仿真,计算飞行过载、射程、最大速度等参数。由于在质量、结构和动力学科均采用了CAD参数化建模,因此计算资源消耗很大,在先前的研究中,已基于现代实验设计技术和支持向量回归机建立了相应学科的近似模型[6],用于替代耗时的高精度模型,替代模型的建立过程和有效性检验均在文献[6]中作了详细描述,文中不再重复叙述。

2.2 导弹学科模型的集成

要将5个学科集成到多学科设计优化框架中,必须对学科间数据流进行详细分析。各学科间数据流向关系如图2所示。

结构外形学科根据任务需求确定导弹各部件的尺寸极限,作为该子学科的设计约束,用以确定这些设计尺寸,同时输出弹体的三维模型。

优化框架将这些设计尺寸参数将作为质量学科的输入参数,以确定起飞质量、燃料质量、质心位置等质量特性相关信息。其中,起飞质量将作为系统级设计目标。

图2 学科间数据流关系Fig.2 Data flow between discip lines

外形参数和质量特性信息将被优化框架输入动力模型中,动力模型根据外形尺寸约束发动机主要尺寸参数的设计,根据燃料质量和特性,计算发动机推力、工作时间等性能参数。

同时,外形尺寸和质心位置信息可输入气动学科进行气动分析计算,确定导弹的升力、阻力系数和力矩系数等气动参数。

至此,通过各学科的分析计算,弹道分析所需数据已经准备完毕,优化框架将其输入弹道学科后进行弹道仿真计算,可确定最大飞行过载、最大舵偏角、最大飞行速度、射程等信息,这些信息将作为系统级的设计约束。通过数据流输入输出分析,就可将这5个学科集成为统一的多学科优化模型,通过优化算法决定设计参数在每一个设计轮次的取值,计算分析系统目标和约束,从而改进下一个轮次的设计,直到优化算法找到全局最优解。

5个学科共确定了17个设计变量,如表1所示。系统性能目标为发射质量最小,系统约束分别为发射质量不超过设计上限,射程不低于设计下限,最大飞行速度不低于设计下限,最大轴向、法向过载不高于设计上限。

2.3 6σ质量控制方法的应用

设X为17维设计向量,并且全部是服从正态分布的随机变量,它们的均值和方差向量分别为U和Δ。根据6σ质量控制理论,非确定性系统性能和约束可表述为

式中 um0为发射质量;σL、σvmax、σNx、σNy分别为下标对应变量的方差;L为射程;vmax为最大飞行速度;Nx和Ny分别为轴向飞行过载和法向飞行过载;下标Llim代表各变量的设计极限。

表1 系统设计变量Tab le 1 Design varab les

3 计算结果

首先,对文中算例进行传统的多学科优化,而后考虑模型的非确定性,进行6σ稳健性优化。文中算例稳健性优化的输入设计参数均值为最优化方案的解,方差为各变量值的1%。根据给定的上下限而言,最优解输入设计变量已满足6σ质量水平,进行6σ稳健性优化后,输入变量依然全部满足6σ质量标准。输出响应结果经过归一化处理后,对比如表2所示。由表2结果可看出,在最优方案下,射程L和最大飞行速度σ水平均未达到要求,其中射程L的σ水平甚至未达到3。因此,从稳健设计的意义上讲并未达标,其长期质量不过关。经过采用6σ质量控制方法进行稳健性设计优化后,这些参数质量均达到了6σ水平。其中,射程方差在最优解的基础上减小了约61%,最大飞行速度方差减小了约57%。

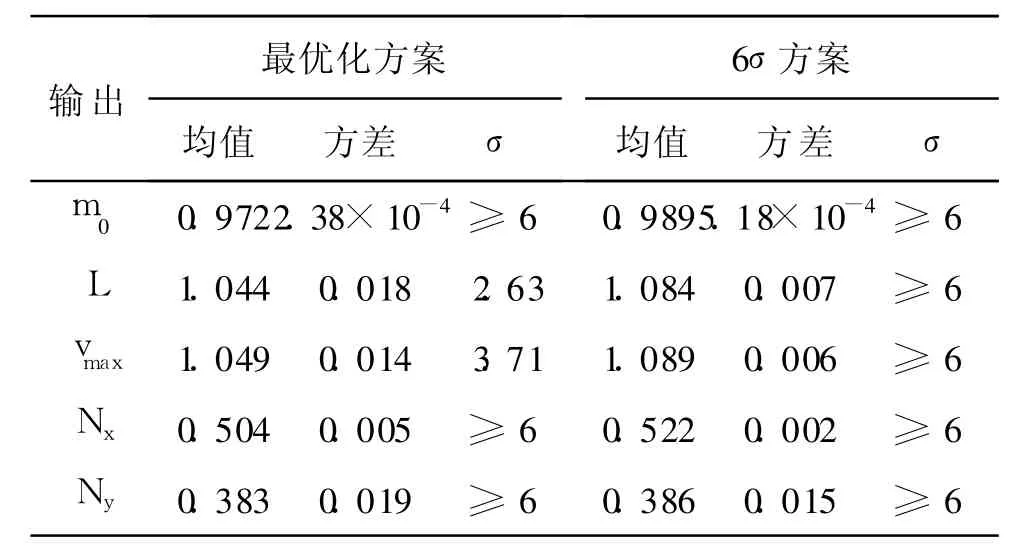
表2 最优化和6σ设计结果输出对比Table 2 Comparision between outputs of op timum and 6σdesign

同时,稳健方案的系统目标均值较最优方案有所提高。可看出,稳健方案与最优方案追求的是完全不同的。6σ质量控制方法为了追求系统的稳健性,适度增加了少量起飞重量,其规范均值由0.972提高到了0.989,这意味着本算例设计目标性能较最优情况降低了设计极限值的1.7%,但却增强了系统对于设计参数波动的承受能力,使系统变得更加可靠,减少了设计失效的可能性。

为了验证结果的实际效果,采用蒙特卡洛方法对2种方案进行1 000次随机仿真试验,假设所有设计变量在均值的基础上有5%的波动,射程和最大飞行速度的响应对比如图3所示。

从图3可见,追求设计目标最优化的方案有大量的设计失效发生,但稳健性方案100%满足了可行性约束。虽然起飞质量稍有增加,也就是放弃了单纯寻找最优目标性能,但却增强了系统的稳健性,使所有产品都达到了设计要求。这在实践中意味着所有的产品可以更好地适应设计参数发生的变化。因此,这样的设计思想应该更具有实际意义。在保证设计可行的前提下,对比可靠性与稳健性的增加,少量的目标性能损失完全可获得更大的效益。

4 结论

(1)对空射巡航导弹概念模型进行最优化设计后,射程和最大飞行速度没有达到质量要求,其σ水平均低于6。经过基于6σ思想的稳健性优化改进后,质量水平全部达标,产品质量趋于稳定。因此,6σ质量控制的思想可有效提高产品设计质量,增强产品质量对设计参数波动的抵抗能力,提高产品的可靠性,更有利于保证产品质量的长期稳定。

(2)在现代国防产品概念设计阶段中尽早引入质量控制方法,从产品设计阶段就开始就考虑产品质量的稳定性,而不是单纯追求系统某些性能的最优,这种思想将有助于提高产品的精细设计水平,尤其在国防工业产品设计中具有一定的推广价值。

图3 最优方案与6σ方案射程及最大速度响应对比Fig.3 Comparision between optimum scheme and 6σ scheme for output range and maximum velocity

[1] Park G,Lee T,Lee K H,et al.Robust design-an overview[J].AIAA Journal,2006,44(1):181-191.

[2] Beyer H,Sendhoff B.Robust optimization-a comprehensive survey[J].Computermethods in app lied mechanics and engineering,2007,196(33-34):3190-3218.

[3] 崔玉莲,刘泌.关于稳健性设计的评述[J].质量与可靠性,1999,79:34-35.

[4] Koch PN.Probabilistic design-optim izing for six sigmaquality[C]//43rd AIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynam ics and Materials Con ference.Denver,Colorado:2002.

[5] Shimoyama K,Oyama A,Fu jii K.Mu lti-objective six sigma approach applied to robust airfoil design for mars airplane[C]//48th AIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics,and Materials Conference.Honolulu,Hawaii:2007.

[6] 马英,何麟书,段勇.基于现代实验设计技术的巡航导弹概念设计[J].北京航空航天大学学报,2008,34(10):1121-1125.