火箭引射模态下一次火箭流量优化方法研究①

吕 翔,刘佩进,何国强,刘 洋

(西北工业大学燃烧、流动和热结构国家级重点实验室,西安 710072)

0 引言

为了保证较高的空气捕获量及良好的发动机性能,火箭基组合循环(Rocket Based Combined Cycle,RBCC)发动机在火箭引射模态下,采用一次火箭对来流空气进行引射增压。在飞行过程中,一次火箭流量将随飞行状态的变化而发生改变[1]。低马赫数飞行时,由于来流空气总压较低,发动机需较大的一次火箭流量,以保证较高的空气引射量;随着飞行马赫数提高,来流空气总压逐渐增大,引射增压所需的一次火箭流量将逐渐降低。因此,获得与飞行状态相匹配的一次火箭流量变化规律,对开展RBCC发动机设计优化、提升发动机性能具有重要意义。

在一次火箭流量变化规律研究方面,国内外研究人员对一次火箭流量与发动机的匹配性及一次火箭流量对发动机性能的影响开展了众多基础研究,获得了一次火箭流量变化对发动机引射性能、推力性能和比冲性能的影响规律,并得到了众多对发动机设计具有指导意义的结论[1-6]。但对实际飞行状态下的一次火箭流量变化规律,目前还缺乏相关研究。文中将从发动机性能最优化角度出发,建立一次火箭流量优化方法,分析飞行条件下一次火箭流量变化规律,为开展一次火箭流量设计提供参考依据。

1 发动机性能优化目标

图1给出了典型飞行状态下一次火箭流量变化对RBCC发动机性能的影响[7]。一次火箭流量为0.1 kg/s时,发动机比冲为482.5 N·s/kg、推力为0.473 kN。尽管比冲为正常情况下火箭发动机比冲的1.5倍左右,但推力却远小于飞行器的气动阻力,飞行器无法实现正常的加速飞行。一次火箭流量为1.5 kg/s时,发动机比冲为209.4 N·s/kg,推力为3.079 kN,尽管发动机推力接近飞行器气动阻力的5倍,飞行器具有良好的加速性能,比冲却低于火箭发动机比冲,无法体现出RBCC推进系统的比冲优势。由此可见,采用比冲或推力作为单一优化目标存在很大的不足,同时也说明了采用比冲和推力进行多目标优化设计时折衷处理的难度。

文献[8]将RBCC飞行工作过程分为多个比冲成线性变化的速度区间[vi,vi+1],并采用式(1)对推进剂质量需求进行计算。

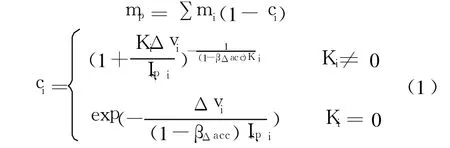
式(1)表明,在速度增量Δvi一定的情况下,影响推进剂质量消耗的关键因素是(1-βΔacc)Isp,即有效比冲。若忽略重力和弹道爬升等因素引起的损失,有效比冲可进一步表示为

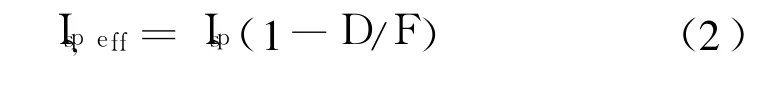
式中 D为飞行器阻力;F为发动机推力。

推进剂质量最小是常用的飞行器总体优化目标之一。根据式(1)可知,对任意弹道实现推进剂质量消耗最小的必要条件是有效比冲最大和飞行弹道最优。因此,以有效比冲作为单目标,开展火箭引射模态下一次火箭流量优化是较合理的选择。

图1给出了有效比冲随一次火箭流量的变化规律。一次火箭流量为0.3 kg/s时,有效比冲最大为206.2N·s/kg,此时发动机比冲为441.4 N·s/kg,推力为1.229 kN,推阻比达到1.88。由此可看出,以有效比冲作为单优化目标,所获得的发动机性能兼顾了高比冲和高推力的设计要求,是替代以推力和比冲进行多目标优化的有效途径。

图1 一次火箭流量对发动机性能的影响Fig.1 Effect of p rim ary rocket mass flow rate on RBCC engine performance

2 一次火箭流量优化方法

式(2)中有效比冲的定义表明,需针对特定飞行弹道和飞行器气动阻力特性,对一次火箭流量进行优化。然而,优化结果得到的发动机性能,将影响飞行弹道分析结果。由此可见,以有效比冲作为优化目标,将导致一次火箭流量优化与飞行弹道计算相互耦合,增加了优化的难度。文中采用试验设计方法,对飞行包线内特定飞行状态进行一次火箭流量优化,建立发动机优化性能表,为开展飞行弹道分析提供性能数据,并根据弹道分析结果,给出了飞行过程中一次火箭流量的变化规律。

实验结果表明[10],空气引射量和二次燃料流量(假定处于氧燃化学恰当比)之间相互影响,存在匹配性问题。对于任意给定的一次火箭流量都存在唯一的二次燃料流量,使燃烧室内达到氧燃恰当比状态,因而进行一次火箭流量优化的同时,必须求解与之相匹配的二次燃料流量。为保证良好的燃烧性能,一次火箭通常处于富燃状态,求解二次燃料流量需充分考虑一次火箭富燃对计算结果的影响。文中采用的计算方法是首先对无二次燃料喷注时发动机内流动状态进行计算分析(所采用的发动机性能分析方法见参考文献[11,12]),获得燃烧室内富氧量m·oxid,rich,并求出与之相对应的二次燃料流量最大值为

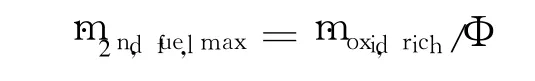
然后,采用如下的比例控制方法,求解出与一次火箭流量相匹配的二次燃料流量。

式中 Υ为氧燃化学恰当比,对于JP-10燃料来说Υ=3.294;K1和K2为增益系数。

过大的增益系数有助于计算结果快速收敛,但易导致计算过程出现振荡或发散;而过小的增益系数,则保证了计算收敛过程的鲁棒性,但缺点是响应较慢。根据大量计算结果,文中取K1=0.4、K2=0.8。

基于上述分析,文中建立了如图2所示的一次火箭流量优化流程。

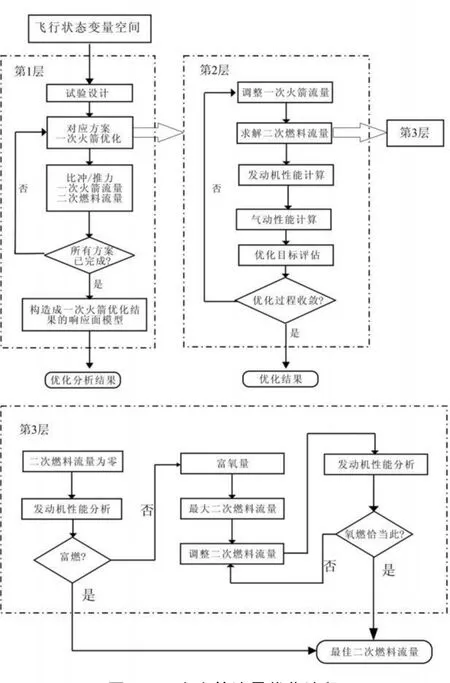
图2 一次火箭流量优化流程Fig.2 Flowchart for primary rocket mass flow rate optimization

优化过程共分为3层:第1层为飞行状态变量空间内一次火箭流量优化,对由试验设计所确定的所有飞行状态(不同的飞行高度H、马赫数Ma和攻角AOA)分别求解最佳一次火箭流量、发动机推力/比冲性能和二次燃料流量;第2层为第1层核心过程的展开,对某一给定的飞行状态进行一次火箭流量优化,并计算发动机各性能参数;第3层则是在给定一次火箭流量条件下,求解与之相匹配的二次燃料流量。其中,第3层求解二次燃料流量采用了如式(3)所示的比例控制方法,第2层进行一次火箭流量优化,则使用了目前广为采用的遗传算法[13],其遗传种群个体数为50,最大遗传代数为2 000,交叉因子为0.9,变异因子为0.2。

3 优化结果分析

对空中载机发射的RBCC飞行器进行了火箭引射模态下一次火箭流量优化及弹道分析[7],该飞行器发射高度为10 km,发射速度Ma0=0.8,火箭引射/亚燃模态转换马赫数为3.0。

整个优化过程分为3步:首先,基于试验设计理论对一次火箭流量优化的计算方案进行了设计(设计结果见表1),各变量的取值范围如下:

第2步,利用图2所示的优化计算流程对每一个计算工况进行了一次火箭流量优化,优化结果如表1所示;最后,利用获得的优化结果进行了飞行弹道分析。

图3给出了弹道分析结果;图4给出了与飞行弹道相对应的单模块发动机一次火箭流量变化规律。

图3 飞行弹道Fig.3 Trajectory for air-launching RBCC

由图4结果可看出,发射初期一次火箭流量较低(0.25 kg/s),随着飞行速度接近于Ma=1.0,一次火箭流量迅速增加至最大(0.75 kg/s),而后开始不断降低。一次火箭流量降低过程所包含的2个较为显著的分界点(即图4中流量曲线斜率较大的点),分别位于Ma=1.0和Ma=1.5附近。由于飞行器跨声速飞行时存在“声障”现象,飞行阻力要高于正常工作条件(阻力系数可高达正常值的2倍[14])。无论是从满足飞行加速度要求,还是从保证有效比冲最大的角度考虑,均需增大发动机推力,一旦突破声障后,发动机推力即可调节为正常工作状态。因此,在Ma=1.0附近形成一次火箭流量最大值。文献[7]的理论分析和文献[2]的实验研究表明,在Ma=1.5附近来流冲压作用占主导地位,对一次火箭流量的需求逐渐降低。与此同时,降低一次火箭流量,还可提高发动机比冲性能,因而在Ma=1.5附近形成了流量骤减现象。超过Ma=1.5后,一次火箭则以较小流量工作(0.22～0.15 kg/s)。根据上述分析及图4所示计算结果,对于文中研究的空中载机发射RBCC方案,选取一次火箭设计状态为最大流量0.75 kg/s、最小流量0.15 kg/s,即流量调节比为5.0。

图4 一次火箭流量Fig.4 Primary rocketmass flow rate

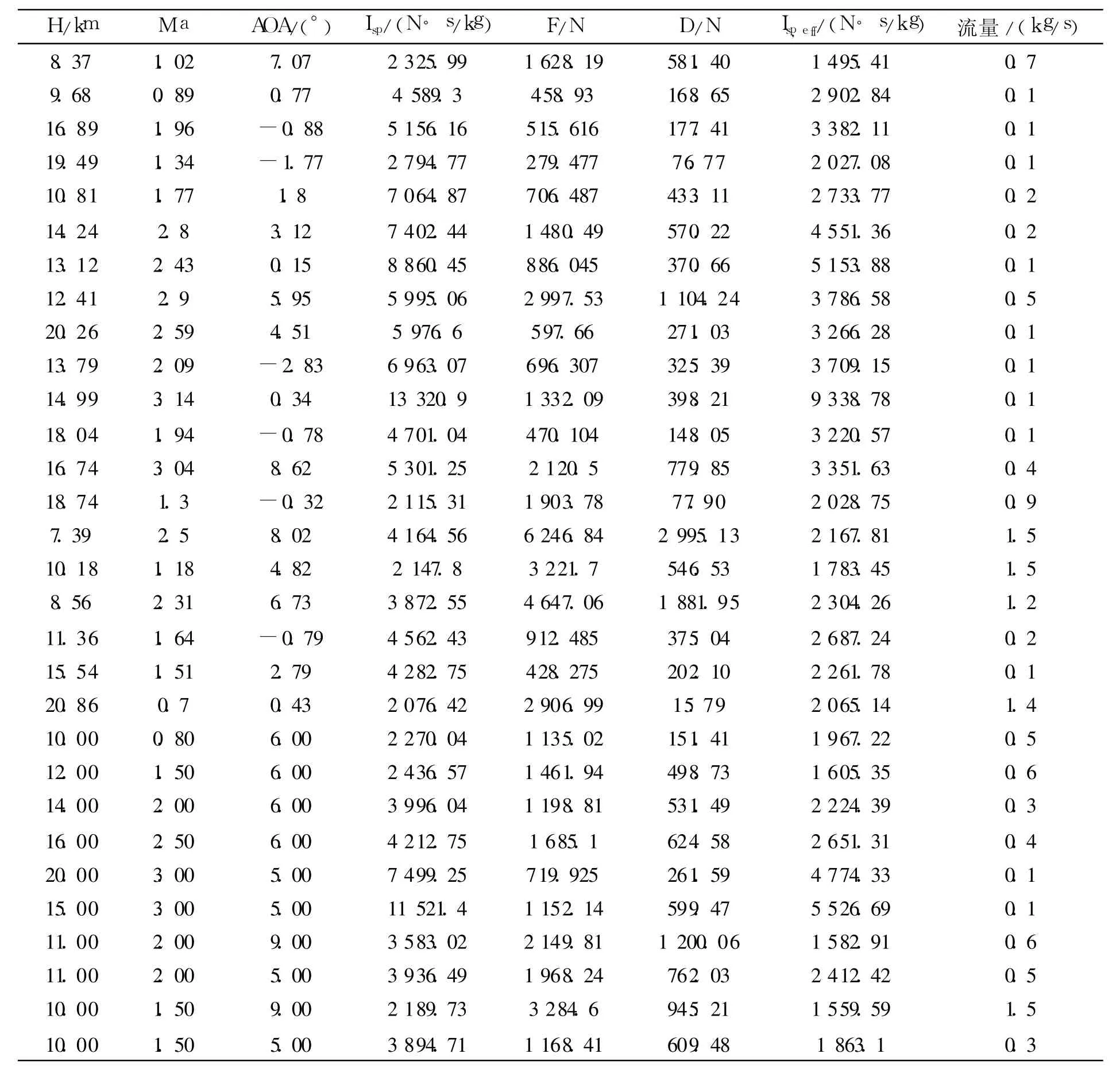
表1 引射模态下一次火箭流量优化结果Tab le 1 Optim ization resu lts o f primary rocketmass flow rate

4 结论

(1)采用有效比冲进行火箭引射模态下一次火箭流量的单目标优化,兼顾了对发动机高推力和高比冲性能的设计需求,并能保证飞行器实现最小的推进剂质量消耗。

(2)建立的一次火箭流量优化方法,考虑了发动机性能优化与飞行弹道分析的相互耦合作用,能有效实现一次火箭流量优化,并给出飞行条件下一次火箭流量的变化规律。

(3)为了克服飞行过程中声障阻力,一次火箭流量在1.0Ma附近达到最大。此时,对发动机提出了较高的推力设计要求。

(4)在1.5 Ma附近,来流空气的冲压作用占主导地位,一次火箭流量出现较大程度的节流。此时,对发动机提出了较高的比冲设计要求。超过1.5Ma后,一次火箭以较小流量工作。

[1] 刘洋,何国强,刘佩进,等.一次火箭流量对RBCC性能影响的数值和实验研究[J].固体火箭技术,2008,31(5).

[2] 李强,刘佩进,李江,等.来流马赫数对引射火箭引射量的影响研究[J].固体火箭技术,2009,32(3).

[3] Line berry D.Fluid mechanics in a non-axisym metric cold flow ejector system[R].AIAA Paper 2004-293.

[4] Namkoung H,Hong C,Moon C,et al.Numerical and experimental investigations on a variable sonic ejector[R].AIAA Paper 2007-5749.

[5] Geunhong Park,Sejin Kwon.The flow p roperties of axissym metric annular bell typeejector-jets[R].Beijing China:Proceedings of the 3rd Asian Joint Con ference on Propulsion and Power,2006.

[6] Jason Etele,Sislian JP,Bernard Parent.Variable area ejectors for increasing the compression factor of an RBCC engine[R].AIAA 2004-3651.

[7] 吕翔.RBCC推进系统总体设计方法研究[D].西北工业大学,2008.

[8] 吕翔,何国强,刘佩进,等.RBCC推进系统总体设计要求评估方法研究[J].宇航学报,2008,29(5).

[9] Thomas M Krivanek,Joseph M Roche and John P Riehl.Affordable flight demonstration of the GTX air-breathing SSTO vehicle concept[R].NASA TM-2003-212315.

[10] 刘佩进,何国强,李宇飞.RBCC引射火箭模态二次燃烧实验[J].推进技术,2004,25(1).

[11] 吕翔,刘佩进,何国强.RBCC发动机性能分析方法研究[J].固体火箭技术,2007,30(2).

[12] 吕翔,何国强,刘佩进,等.RBCC发动机性能分析模型改进方法研究[J].固体火箭技术,2010,33(4):387-390.

[13] 周明,孙树栋.遗传算法原理及应用[M].北京:国防工业出版社,1999.

[14] Brock M.Performance study of two-stage-to-orbit reusable launch vehicle propulsion alternatives[D].Aeronautics and Astronautics Dept.,AFIT,Wright-Patterson AFB,2004.