基于优化RBF神经网络的缝纫平整度客观评价
2010-01-25吴懋刚潘永惠
吴懋刚,潘永惠,范 蕤
(江阴职业技术学院 计算机科学系,江苏 无锡 214405)
服装缝纫平整度是影响服装外观质量的重要因素,随着服装生产自动化程度的加强和市场对服装生产企业快速反应能力要求的日益提高,服装缝纫性能的客观评价也逐步成为纺织服装界关注和研究的重点[1-2].目前在大多数商业行为中仍然以主观评定法AATCC—88B作为服装缝纫平整性能的主要评价标准.该评价方法的特点是直接、简单、投入少、易掌握,然而这种方法是在参考样品的基础上目视评级,易受到评价者个人的不确定因素的影响而有失客观性.随着计算机技术的飞速发展,图像处理及计算机模拟技术开始应用于缝纫外观的识别和评价模型[3-4].由于丝织物缝纫对小负荷区域的力学性能很敏感,其在低应力下的各项力学性能与加工生产有着密切的关系.本文主要研究了丝织物的各项FAST力学性能指标与缝纫平整度等级之间的关系,并提出了一种基于优化RBF神经网络的丝织物缝纫平整度客观评价方法.
1 RBF神经网络
1.1 RBF神经网络学习算法
RBF神经网络的结构如图1所示.它由输入层、隐层和输出层三层结构组成[4].网络的输出按如下公式计算:
(1)
其中,x∈Rn是一个输入向量,φk(·)是从R+(所有正实数的集合)到R的函数.wik是输出层权值,N是隐含层的神经元数目,ck是输入向量空间的RBFNN中心.公式(1)可以写为:
(2)
其中,‖·‖2表示欧几里德范数.对于隐含层的节点神经元,需要计算与它相关的中心和网络输入之间的欧几里德距离.隐含层节点的输出是距离的一个非线性函数.网络的最后输出为隐含层每个节点输出的加权和.
RBF神经网络隐层节点的非线性函数φk(·)的取值一般为高斯径向基函数:
φk(x)=exp(-‖x-vk‖2/ 2σk2)
(3)
其中vk和σk分别是第k个隐层节点的中心向量和宽度.由于高斯函数是一中径向对称函数,当输入信号越靠近基函数中心时,隐层节点的输出值就越大,越远离中心时,节点的输出就越小.从第k个隐层节点输出的最大值到最小值的收敛半径也称为基函数的宽度是由σk控制的.
RBF神经网络隐层节点非线性函数的特点很好模拟了人类大脑皮层中局部调节和交叠的感受野的反应特点,使网络的输入信号可以在局部产生响应,因此,RBF神经网络具有局部逼近能力[5].
φi(xk)=φ(‖xk-vi‖)
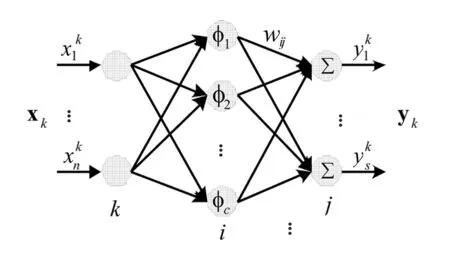
图1 RBF神经网络结构
1.2 优化RBF神经网络算法
在RBF神经网络中隐层节点的基函数确定后,重要的就是确定基函数的中心vk(中心向量)、基函数的宽度σk和输出层权值wik[6].经典的RBF神经网络的中心确定有三种常见的方法,即根据经验选择可以代表训练样本分布性能的基函数中心、利用聚类的方法选择基函数中心和运用误差纠正算法进行可监督学习.当中心确定好之后,经典径向基网络的基函数宽度σ通常按如下公式计算:
(4)
其中,其中dmax是选择的中心之间最大欧几里德距离,K是中心的数目.
本文在对经典的RBF径向基网络运用的过程中对其进行优化,以改善神经网络对丝织物缝纫性能预测的效果.优化神经网络算法如图2所示.
使用MATLAB实现算法的基本步骤如下:
1)初始化.运用模糊核聚类算法(KFCM)计算得到模糊聚类中心和模糊分割矩阵,将其作为RBF网络的基函数中心和宽度调节的输入.
2)利用高斯函数公式(3)计算隐层节点的输出权值.
3)运用伪逆算法计算隐层节点到输出层的连接权值.
4)计算网络的输出结果,即缝纫性能客观评价等级值.
优化的径向基神经网络运用聚类算法(KFCM)得到基函数的中心C和模糊分割矩阵μ,并将μ作为RBF网络控制基函数宽度的调节参数,从而使网络隐层节点具有更好的受控感受野.
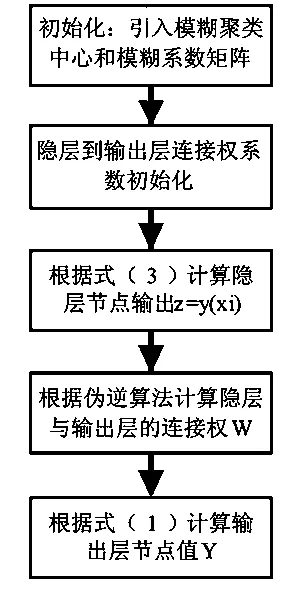
图2 RBF神经网络算法
2 实验结果
本文采用FAST(Fabric Assurance by Simple Testing)一起对丝织物25项物理力学性能进行测试,对其成形性、加工型和尺寸稳定性等性能进行预测.选用了30块常用薄型丝织物作为试验样品,基本规格参数如表1所示.
将测试样品裁成尺寸为30cm×6cm的缝条,上下缝条沿同一丝缕方向从中间进行缝纫,仅考虑上下缝条为同丝缕方向时的缝纫平整度评级.
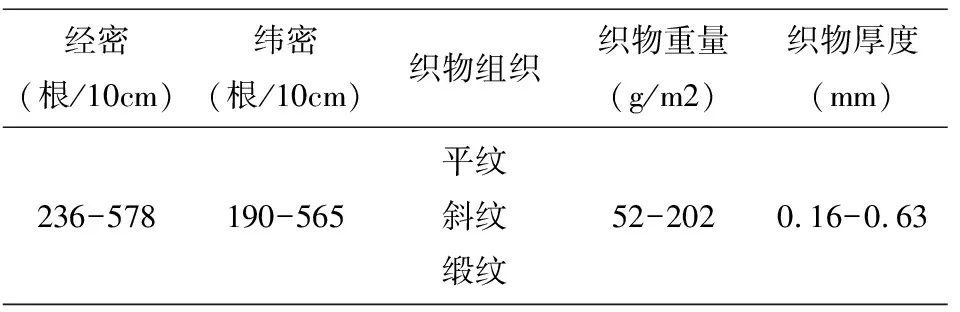
表1 实验样品的基本参数
本文主要考察薄型丝织物的力学性能参数对缝纫性能的影响关系[3],不考虑缝纫条件的变化对面料的缝纫性能的影响.样品的缝制由服装厂的熟练技术工人采用相应的工业平缝机进行缝制,所采用的各项缝制条件见表2所示.

表2 样品缝制时针、线配用标准
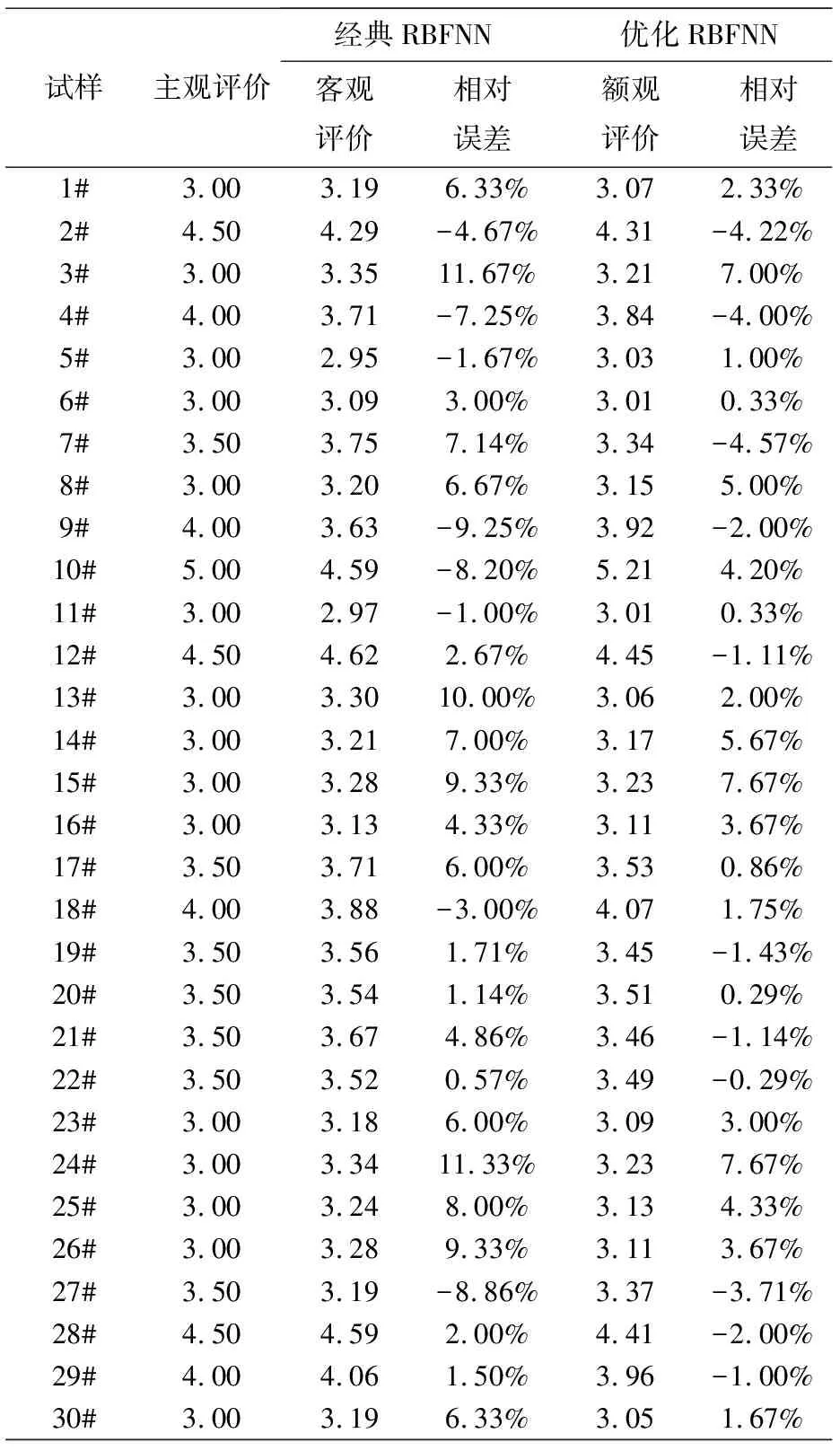
表3 经典RBF与优化RBF神经网络预测结果
在对样品缝条进行缝纫时,根据工厂实际生产经验,采用相应缝纫条件对不同缝条进行缝制加工.对缝纫好的样品经过标准洗涤晾干后参照AATCC-88B标准由两位专家对每块缝条进行主观评级,取其平均值.分别沿5个不同方向(经向到纬向:0°,30°,45°,60°,90°)进行缝纫评级,并测量计算相应的力学性能指标值,每类面料得到150组实验数据,其中120组作为网络训练建模,另外30组用于模型精度检验.分别采用经典RBF网络和优化RBF网络对丝织物面料缝纫平整性能的主客观评价结果进行分析,如表3所示.
为了更清楚表示两种网络预测的效果,对表3中的实验结果进行相关性分析,如图3所示.
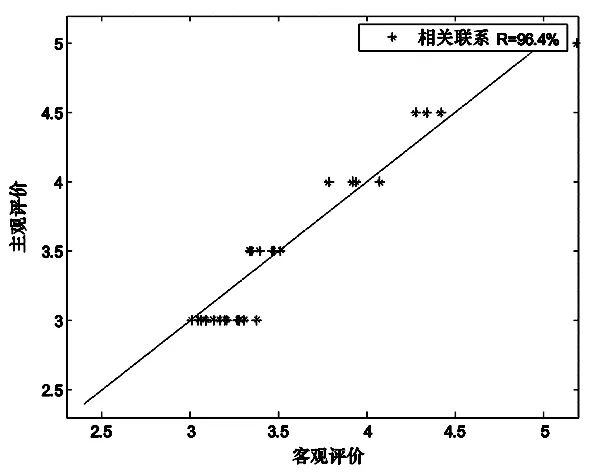
图3 优化RBFNN的主客观评价相关性分析
图中显示基于优化RBF神经网络对丝织物面料缝纫性能的主客观预测的相关性数据,该方法的整体预测精度达到96.4%,表明本文所提出的基于优化RBF神经网络具有较好的预测能力.
3 结束语
本文综合运用聚类的模式识别方法和径向基神经网络学习算法提出了一种优化的RBF神经网络模型.该模型在对丝织物面料的缝纫平整度客观评价系统应用中,体现出其客观、快速、高效的评价性能.但是,由于本文实验所用试样的数量仍不够丰富和全面,丝织物材料种类众多,结构复杂,选样时不可能做到面面俱到,大多数试样为常用材料和常用结构,所建系统的应用范围也仅局限于和测试用面料同类或相近的面料,因此如何提高本文模糊辩识系统的泛化能力,将是今后进一步研究工作的重点.
参考文献:
[1]刘侃.面料缝纫平整度客观评价新方法[J].纺织导报,2007(12):96-97.
[2]Pan Y H,Bao F,Wang S T.Objective evaluation of seam pucker using SFC-RBFNN[J].DCABES 2007 Proceedings,2007,1:592-596.
[3]杨建忠,王善元.轻薄织物斜向力学性能与缝纫起皱关系的研究[J].西北纺织工学院学报,2001,15(3):15-20.
[4]Yang Y P,Xu X M,Zhang W Y.Design neural networks based fuzzy logic[J].Fuzzy Sets and Systems,2000,114:325-328.
[5]沈谦,王涛.结构优化的RBF神经网络学习算法[J].微电子学与计算机,2000(4):14-18.
[6]Yan S,MaSaHaru Mizumoto.A new approach of neuro-fuzzy learning algorithm for tunning fuzzy rules[J].Fuzzy Sets and Systems,2000,112:99-116.
