二维同心圆环弹子球体系的量子谱分析
2010-01-25张业兵张延惠
张业兵,张延惠
(1.淄博师范专科学校 物理系,山东 淄博 255130;2.山东师范大学 物理与电子学院系)
激光理论和技术的发展极大地改变了原子、分子物理学的面貌,人们研究介观物理领域的焦点由侧重体系能级结构转向其相关动力学性质的研究,自从Gutzwiller提出态密度的周期轨道理论以来[1],用半经典的方法来研究粒子的经典运动已成为处理某些量子问题必不可少的工具.近年来,纳米器件、微腔结构及其输运问题[2]已经成为人们研究的前沿课题.而量子台球可以作为研究它们的理想模型,在可积或量子混沌系统中,对理论和实验都具有很好的指导作用.人们应用周期轨道理论已经研究了许多体系中一个粒子量子化的本征值谱和经典轨道之间的对应关系[3-5].本文应用半经典周期轨道理论的思想,通过定义量子谱函数,研究了量子台球在二维圆环无限深势阱体系中的经典轨道与量子谱的关系,并把这些轨道和体系的傅立叶变换量子谱的峰值位置一一对照.
1 量子谱函数
一个质量为μ的粒子(为了避免与大家熟悉的量子数相混淆,此处用μ来表示粒子的质量),假设体系的Hamiltonian是:
(1)
在无限深圆环体系势阱中(如图1),设外半径为Rout=R,内半径为Rin=R(0<<1),
其对应的势能可表示成:
(2)
对应的定态Schrödinger方程是:

图1 同心圆环
(3)
其中本征能量和本征函数分别为En和ψn,n为标记量子态量子数.由于满足边界条件,在边界处:
(4)
在周期轨道理论中,最主要的物理量是量子能态密度:
(5)
式(5)中的求和包括所有的定态的能量本征值.周期轨道理论的一个主要结论是,量子能态密度可以写成半经典形式:
(6)
式中的第一项ρ0(E)是一个平滑的背景项,随能量E的变化,ρ0(E)变化非常缓慢,因此这一项对态密度的贡献为常数.第二项是最关心的振荡项,Sr(E)为轨道的经典作用量,对应着所有的基本轨道(γ=1,…,∞),ρ表示基本轨道的多次回归(p=1,…,∞).φr是在路径积分过程中引入的相位修正.
假设势阱的面积为A,势阱的周长为L,在边界上体系的波函数ψ=0,这样平滑的背景项ρ0(E)就可以表述为:

(7)
利用公式(5),在动量空间中,忽略一些不重要的因素,可以得到相等的态密度:
(8)
与公式(6)相应的表示,在动量空间中就可以写成:
(9)
上式两边同时乘以eikL,并对整个动量空间积分,可以得到离散的能量项:
(10)
对于半经典的振荡项,经过傅立叶变换之后,得到:
(11)
从上式可以看到在δ函数的峰值出现的地方,对应着经典轨道L=ρLr的长度.
在(10)式中,因为计算量的限制,不可能取无穷多的数值,只能取有限量的数值来计算.因此(11)写成:
(12)
2 二维圆环弹子球体系的量子表达
一个质量为μ的弹子球在两维圆环体系中运动,在极坐标系下定态Schrödinger方程为:
(13)
假设分离变量解的形式是ψ(r,θ)=R(r)Θ(θ),由此得到角向方程和径向方程分别为:
(14)
(15)

归一化的角向方程解的形式是:
(16)
角动量本征的值为:L=mħ
(17)
其中m=0,±1,±2,±3,…是角动量量子数,“+”和“-分别表示弹子球沿逆时针和顺时针运动.
令z=kr,径向方程变为:
(18)
此方程为m阶柱贝塞耳方程,通解是第一类贝塞耳函数和第二类贝塞耳函数的线性组合:
R(z)=αJm(z)+βNm(z)=αJm(kr)+βNm(kr)
(19)
其中Jm(z)称为m阶第一类贝塞耳函数(又叫柱贝塞耳函数),Nm(z)称为m阶第二类贝塞耳函数(又称诺依曼函数),αβ为线性系数.
由Dirichlet边界条件,
可以得到:
R(km,nrfR)=αJm(km,nrfR)+βNm(km,nrfR))=0
R(km,nrR)=αJm(km,nrR)+βNm(km,nrR))=0
(20)
消去系数α、β得径向本征方程:
Jm(km,nrfR)Nm(km,nrR)-Jm(km,nrR)Nm(km,nrfR)=0
(21)
从而可得本征能量为:
(22)
其中,a(m,nr)=km,nr/R是方程(21)m阶的第nr个零点.
由此得到径向波函数:
(23)
此处归一化系数Am,nr满足:
(24)
由此就可以得到圆环体系势阱中弹子球的能量本征波函数:
(25)
3 二维圆环弹子球体系运动的经典表达
一个质量为μ的弹子球,在二维无限深圆环体系势阱中运动,γmin表示运动的路径与圆心的最短距离,弹子球与内圆和外圆发生碰撞时遵循反射定律,则经典的周期轨道的长度可以用n,p,q三个整数表示,其中n=1,2,3…为回归的次数,p=1,2,3…为粒子与外圆碰撞的次数,q=1,2,3…为粒子第一次回到初始点粒子转的圈数,要求p≥2q.粒子运动的经典的周期轨道的长度,可以分下列两种情况讨论:
(1)第一种情况,粒子没跟内圆发生碰撞:
γmin表示路径到圆心的最短距离,这种情况与势阱为圆的情况相同,(图2为p=5,q=1的情况),此时的要求为:
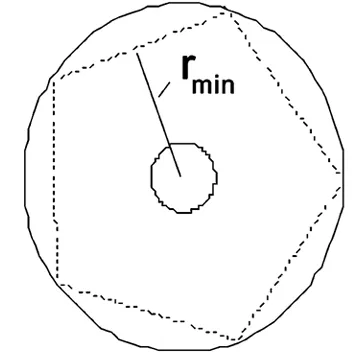
[5,1]

(26)
此时轨道的长度为:
(27)
如果q不变,p无限增大,当p→∞时,运动接近圆周运动,当q=1时,其轨道的总长度就是圆的周长,q≠1,其轨道的总长度就是圆的周长整数倍即2πR,4πR,6πR……:
L1(n;p→∞,q)=n2πR
(28)
(2)第二种情况,粒子跟内圆发生碰撞,又分为两种情况.

(29)
图3为p=5,q=-1,负号表示粒子与内圆发生了碰撞,p,q与图2值相同,但是与内圆发生碰撞的.
几种特殊情况:第一,粒子运动路径与内圆相切,f=cos(πq/p),则此种情况的轨道长度也为(27)即:
L2(n;p,q,f=cos(πq/p))=L1(n;p,q)
(30)
第二,粒子由外圆上的某点出发,经内圆反射后直接按原路径返回到出发点(对应着[p,q]=[2,1])以及这种方式的多次回归情况(back-and-forth),此时角动量的粒子数为零,即m=0,这种

[5,-1]
情况轨道的长度为:
L3(n;f)=n[2(1-f)R]=L2(n;2,1,f)
(31)

(32)
如果q不变,p→∞时,对应着弹子球回到初始点在内外圆之间经过了无限次碰撞,其轨道的总长度为:

(33)
4 量子谱与经典轨道的对应
通过上面的讨论,写出了粒子在二维圆环体系几种典型情况经典运动的轨道长度,求出了粒子在二维圆环势阱体系量子波函数和能量本征值,又利用周期轨道理论和傅利叶变换写出了量子谱函数的表达式,下面通过计算来寻找经典与量子的对应.

经典具体轨道如图5所示,方括号内两个值中第一个为弹子球与外圆碰撞的次数,后面一个值为粒子从初始点出发第一次回到初始点所转的圈数,有负号表示与内圆发生了碰撞:

图4 f=0.2时圆环体系量子谱与经典轨道的对应

图5 f=0.2圆环体系,弹子球运动的部分经典轨道
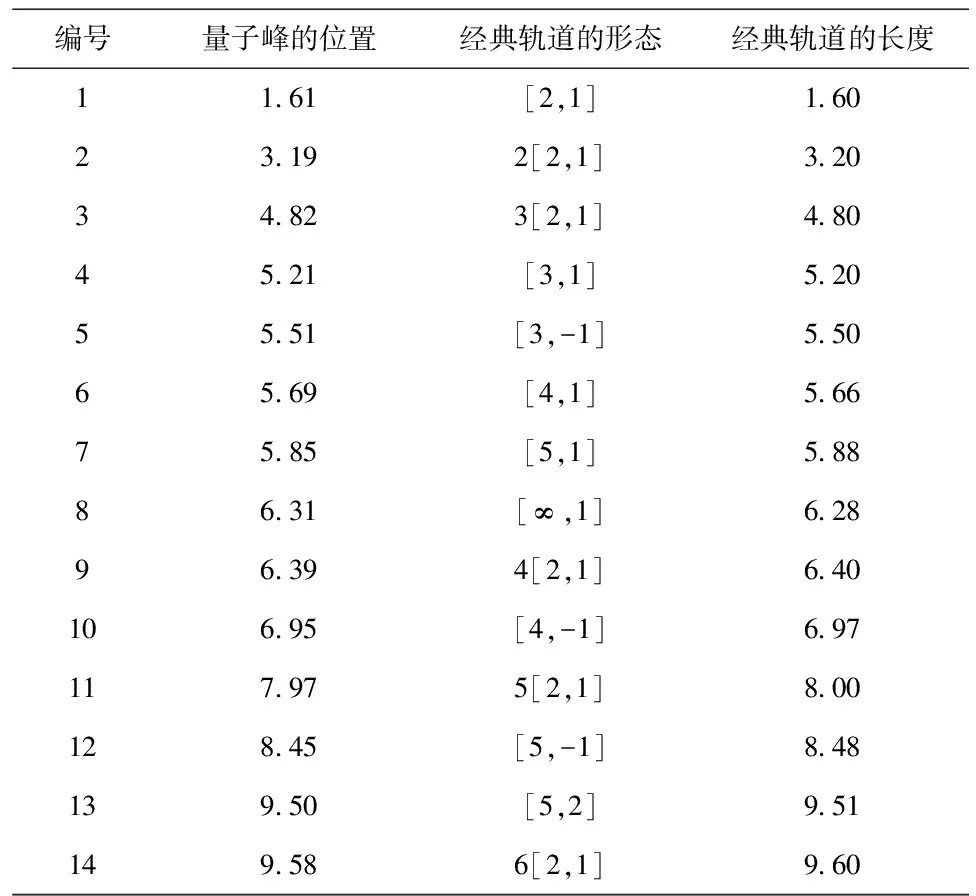
编号量子峰的位置经典轨道的形态经典轨道的长度11.61[2,1]1.6023.192[2,1]3.2034.823[2,1]4.8045.21[3,1]5.2055.51[3,-1]5.5065.69[4,1]5.6675.85[5,1]5.8886.31[∞,1]6.2896.394[2,1]6.40106.95[4,-1]6.97117.975[2,1]8.00128.45[5,-1]8.48139.50[5,2]9.51149.586[2,1]9.60
表1是圆环中弹子球体系的量子谱傅立叶变换峰的位置与经典轨道的对照,从图4,图5和表1可以看出,把经典轨道与傅立叶变换量子谱进行对照,在误差允许的范围内,经典轨道与傅立叶变换量子谱有很好的对应,每条峰都对应着一条和几条经典的轨道.各种量子峰的高度是不同的,量子峰的高低反映其对应经典轨道的条数的多少.
5 结论
本文利用分离变量法求出了二维无限深势阱圆环弹子球体系的本征值和本征函数,给出精确的数值解.应用几何的方法根据不同情况,分别给出了经典轨道的信息(形状、轨道长度),并把这些轨道和体系的傅立叶变换的量子谱的峰值一一对照.又计算出了当Rin=0.2时,不同情况的经典轨道的长度,通过比较它们的傅立叶变换谱和经典轨道,结果发现量子谱的峰位置与经典轨道的长度在误差允许的范围内符合的很好,为了便于理解,分别画出了量子谱的图像、经典运动的轨道图像,列出了二者的对应表,这些特点可以通过这些表和图清晰、直观的显现出来.从而证明了周期轨道理论的正确性,进一步说明半经典理论为经典和量子力学提供了很好的桥梁作用.这种理论可以用来解释光谱学中强电磁场中的原子结构,微腔输运中的相关技术,半导体微结设计的连接,尤其在是两维或是三维弹子球系统中[6-8],由于半导体器件中电子的输运性质依赖于腔体的形状,因此对圆环弹子球体系的动力学性质的研究,在未来还有较高的应用价值.
参考文献:
[1]Gutzwiller M C.Periodic orbits and classical quantization conditions[J].J.Math.Phys.,1971,12:343.
[2]T.Blomquist,et al.Time-resolved dynamics of electron wave packets in chaotic and regular quantum billiards with leads[J].Phys.Rev.,2002,E66:026217.
[3]R.W.Robinett.Visualizing classical periodic orbit from the quantum energy spectrum via the Fourier transform:simple infinite well examples[J].Am. J.Phys,1997,65:1167-1175.
[4]R.W.Robinett.Visualizing the solutions for the circular infinite well in quantum and classical mechanics[J].Am.J.Phys.,1996,64:440-445.
[5]R.W.Robinett.Periodic orbit theory analysis fo the circular disk or annular billiard:Nonclassical effects and the distribution of energy eigenvalues[J].Am.J.Phys.1999,67:67-77.
[6]陆军,杜孟利.从量子谱到经典轨道:矩形腔中的弹子球[J].物理学报,2004,53(8):2450-2453.
[7]Lin Sheng-Lu,Gao Feng,et.al.Quantum Spectra and Classical Orbits in Two-dimensional Equilateral Triangular Billiards[J].Chin.Phys.Lett.,2005,22:9-11.
[8]Zhang Y H,Zhang L Q,Xu X Y,Ge M H,Lin S L,Du M L.The quantum spectra analysis of the circular billiards in well[J].Chin Phys,2005,15(3):502-506.
