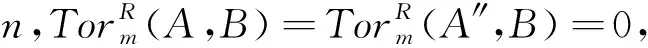探研极大平坦维数

于梅菊,方咏梅

(通化师范学院 数学系,吉林 通化 134002)

1 引言

维数的研究是同调代数的一个主要内容,其研究对环与模的结构都十分重要,给定一个环或者模,我们可以通过它们的维数对它们的特征进行刻画.伴随同调理论的形成，同调维数便一直成为同调代数中研究的焦点.受文献[1-3]中提出的极大投射模、极大内射模和极大平坦模的概念启发，本文引入了R-模M的极大平坦维数(记作max.fd(M))的概念,证明了R-模M是极大平坦模的充分必要条件是max.fd(M)=0,并且研究了极大平坦维数的一些性质,得到了一些比平坦维数更好的结论，在此基础上给出了对半遗传环、遗传环、正则环的刻画.

本文所讨论的环都是带有单位元1的结合环，模指酉模，M*=HomZ(M,Q/Z).

2 主要结果

定义1[3]设M是右R-模,若对任意左R-模正合列0→A→B→C→0,其中C是单模,有0→M⊗A→M⊗B→M⊗C→0正合,则称M是极大平坦模.

显然，平坦模是极大平坦模；环R作为右R-模是极大平坦模.

由于每个右R-模M都有平坦分解,而平坦模是极大平坦模,所以每个右R-模M都有一个极大平坦分解,即存在正合列…→Fn→…→F1→F0→M→0,其中每个Fn都是极大平坦模.

定义2 设右R-模M有如下形状的极大平坦分解

…→Fn→…→F1→F0→M→0,

则在M的所有这种形状的极大平坦分解中,必有一个极大平坦分解,其中的非负整数n是最小的,这个最小的n称为右R-模M的极大平坦维数,记为max.fd(M)=n.若上述的n不存在,则记为max.fd(M)=∞.

显然，对任意的右R-模M,有max.fd(M)≤fd(M).

定义3 称r.max.fd(R)=sup{max.fd(M)/ ∀M∈MR}为环R的右极大平坦维数,同理可以定义左极大平坦维数l.max.fd(R)=sup{max.fd(M)/∀M∈RM}.

显然，对任意环R,有r.max.fd(R)≤r.fd(R).

定理1 若右R-模M是极大平坦模⟺max.fd(M)=0.

证明 因为M是极大平坦模,则M有极大平坦分解0→…→0→F0→M→0,其中F0=M,Fi=0(i≥1),那么max.fd(M)=0；反之设max.fd(M)=0,则M有一个极大平坦分解0→…→0→F0→M→0,其中Fi=0(i≥1),因此F0≅M,故M是极大平坦模.

定理2 设M是任一右R-模,则下列条件是等价的:(1)max.fd(M)≤1;(2)极大平坦模的子模是极大平坦模;(3)有极大平坦模F0,F1使M≅F0/F1.

证明 (1)⟹(2) 对任一右R-模M,有max.fd(M)≤1,设F0是极大平坦模,F1是F0的子模,则有正合列0→F1→F0→F0/F1→0,由于max.fd(F0/F1)≤1,则F1是极大平坦模.

(2)⟹(1)设M是任意右R-模,则有自由模F0,使正合列0→F1→F0→M→0成立,因为F0是极大平坦模,由条件(2)可知F1也是极大平坦模,则有max.fd(M)≤1.

(1)⟺(3)显然.

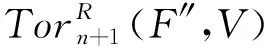
证明 用函子-⊗V作用正合列,0→F′→F→F″→0得长正合列

定理5 设M是一个右R-模,则下列叙述是等价的:

(4)⟹(3)显然.

(3)⟹(2)令As=Im(Fs→Fs-1),由序列0→X→Fn-1→…→F1→F0→M→0正合,使得以下正合序列

0→A1→F0→M→0,
0→A2→F1→A1→0,…,
0→An-1→Fn-1→An-2→0,
0→X→Fn-1→An-1→0,

正合，因为每个Fi都是极大平坦模,由定理3可知有下面的正合列

于是有

由引理1可知X是极大平坦模.

(2)⟹(1)对于任意右R-模M,可以构造正合列0→X→Fn-1→…→F1→F0→M→0,其中X=ker(Fn-1→Fn-2)，且每个Fi皆是极大平坦模,由已知X也是极大平坦模,故max.fd(M)≤n.

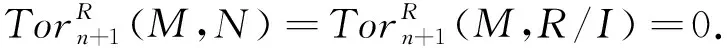
由定理5可以得到如下推论.

定理6 对任意环R,rmax.fd(R)=sup{fd(R/I)/I是R的极大左理想}.

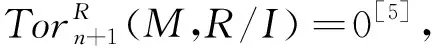
定理7 设0→A→A′→A″→0是右R-模正合列,则

(1)若max.fdA,max.fdA′,max.fdA″中有两个是有限的,则第三个也是有限的,并且若max.fdA>max.fdA″，必有max.fdA′=max.fdA.若max.fdA

(2)若A.A″是极大平坦模,则A′也是极大平坦模；若A是极大平坦模,A″不是极大平坦模且max.fdA″有限,则max.fdA″=max.fdA′+1.

证明 (1)对任意单左R-模B,任意n≥0,有正合列

因此,若max.fd(A)，max.fd(A′)，max.fd(A″)中有两个是有限的,则第三个也是有限的.

(2)若A，A″都是极大平坦模,则max.fd(A)=max.fd(A″)=0,由(1)得max.fd(A′)≤max.fd(A″)即max.fd(A′)≤0,所以max.fd(A′)=0,即A′是极大平坦模；若A是极大平坦模,A′不是极大平坦模,则max.fd(A)

定理8 对任意环R,max.fd(R)≤WD(R).

证明 对任意右R-模M,若fd(M)=n,则存在M的一个平坦分解0→Fn→Fn-1→…→F1→F0→M→0,又因为平坦模是极大平坦模,因此上述平坦分解也是极大平坦分解,从而由极大平坦维数的定义有max.fd(M)≤fd(M)=n,所以max.fd(R)=sup{max}.fd(M)/∀M∈MR}≤WD(R)=sup{fd(M)/∀M∈MR}.

定理9 设R是遗传环,则max.fd(R)≤1.

证明因为R是遗传环,则由文献[8]可知WD(R)≤1,又由定理8知max.fd(R)≤WD(R),所以max.fd(R)≤1.

定理10 设R是半遗传环,则max.fd(R)≤1.

证明 同定理9.

定理11 设R是Von Neuman正则环,则max.fd(R)=0.

证明 因为R是正则环,则由文献[8]可知WD(R)=0,再由定理8可知max.fd(R)=0.

参考文献：

[1]罗荣,汪明义.关于极大投射模[J].四川师范大学学报,2000,28(4):405-408.

[2]ZHAO Guo,WANG Ming-yi.Some Notes On Maximal Injectivity[J].四川大学学报,2005,42(5):859-866.

[3]王良.极大平坦模与极大平坦维数[J].湖南人文科技学院学报,2006,90(3):18-20.

[4]程福长,易忠.环的同调维数[M].桂林:广西师范大学出版社,2000.

[5]周伯埙.同调代数[M].北京:科学出版社,1999.

[6]Anderson F.W.,Fuller K.R.Rings and categories of modules[M].New York:Sp ringer2Verlag,1974.

[7]Rotman J.J..An introduction to Homological Algebra[M].New York: Academic press,1979.

[8]张力宏.基础环论[M].长春:吉林大学出版社,1993.