小攻角条件下动能弹体高速侵彻混凝土靶的弹体弯曲*

王一楠，黄风雷，段卓平

（北京理工大学爆炸科学与技术国家重点实验室，北京 100081）

小攻角条件下动能弹体高速侵彻混凝土靶的弹体弯曲*

王一楠，黄风雷，段卓平

（北京理工大学爆炸科学与技术国家重点实验室，北京 100081）

将高速侵彻混凝土靶板的弹体简化为自由梁，应用弹体侵彻阻力和梁动态弯曲内力分析了由小攻角产生的横向载荷导致的弹体弯曲。结果表明，弹体理论弯曲条件受弹体着靶前状态、弹体结构和材料控制。理论计算证实弹体高速侵彻混凝土靶板时由于小攻角的存在会发生弹体弯曲变形，弹体侵彻实验结果表明弹体弯曲位置和弯曲条件与理论分析结果相符。

爆炸力学；弹体弯曲；高速侵彻；动能弹体；混凝土靶

1 引 言

侵地武器是打击摧毁重要地下军事目标的有效武器，战斗部通过侵入地下并在预定深度爆炸以摧毁深层目标。由于许多地下工事采用混凝土作为防护手段，因此动能弹体深侵彻混凝土成为研制侵地武器的重要方向之一，同时也是冲击工程界的热门课题。

随着防护手段与军事需求的发展，对侵地武器的要求也不断提高，研究重点逐渐由一般动能侵彻弹（弹体初速度vs≤1km／s）向高速侵彻弹（1km／s＜vs≤2km／s）过渡。由于侵彻弹体材料与混凝土之间跨数量级的强度差异，常把初速度低于1km／s的动能弹体近似为刚体进行分析。学者们［1－11］在该领域进行了大量的研究工作，建立了弹体侵彻靶板的理论分析模型。X.W.Chen等［12－15］在M.J.Forrestal等工作的基础上提出了控制弹体侵彻靶板的2个量纲一参数，扩展了Forrestal侵彻模型的应用范围，进一步发展了刚性弹体侵彻／穿甲动力学。然而当弹体初速度高于1km／s后，出现了弹体头部严重侵蚀，弹身弯曲，终点弹道偏转以及弹体破裂等现象，刚性弹体的假设不再有效。由文献［16］关于侵地武器的研究范围，对于高速侵彻弹，应把弹体作为可变形／侵蚀弹体进行分析。

本文中，在刚性弹体受力模型的基础上，对动能弹体高速侵彻混凝土靶板出现的弹身弯曲现象进行理论分析，并与实验结果进行对比，验证结果的有效性。

2 弹体侵彻阻力模型

基于混凝土材料的动态球形空腔膨胀分析［17］，刚性弹体正侵彻混凝土靶板的侵彻阻力

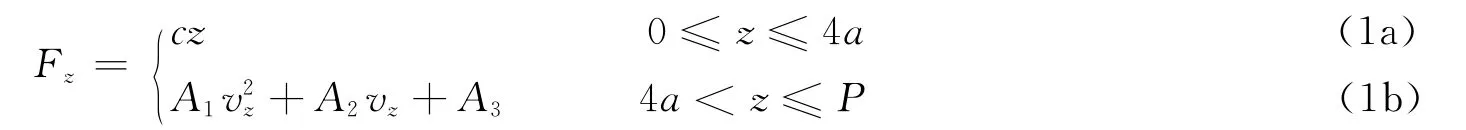
式（1a）、（1b）分别对应动能弹体正侵彻混凝土靶板过程的开坑阶段与孔道阶段［5，12－13］，如图1所示。式中：z是弹体运动方向的位移坐标；c是常数，表示开坑阶段的阻力随侵彻深度增加而升高；vz是弹体的即时速度；A1、A2和A3是混凝土动态球形空腔膨胀压力参数与弹体头部形状积分获得的正侵彻阻力参数。图1中的v1和t1分别表示开坑阶段结束或孔道阶段开始的弹体速度和时刻，P是总的侵彻深度。如图2所示，对于弹体头部轮廓函数为y＝y（x）的任意头部形状弹体，阻力参数为［12］

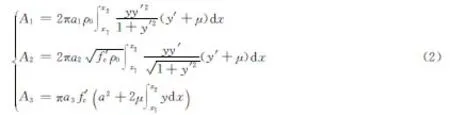
式中：a1、a2和a3是动态球形空腔膨胀压力参数［17］；a是弹体半径；f′c是混凝土的无围压单轴抗压强度；ρ0是混凝土的初始密度；μ是弹体与混凝土之间的动摩擦因数；y′＝dy／dx。式（1）、（2）涵盖了侵彻弹体常用的卵形头部的阻力模型。图2中x1和x2是弹体头部的轴向坐标，b是弹体头部长度。

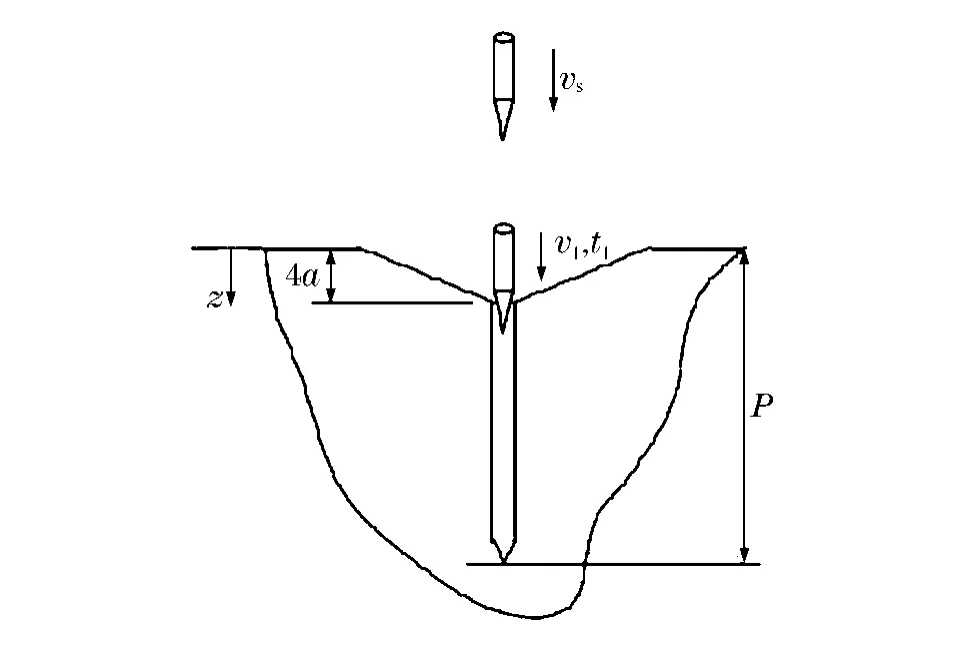
图1 弹体侵彻混凝土过程示意图Fig.1Penetration process of concrete

3 弹体弯曲理论分析

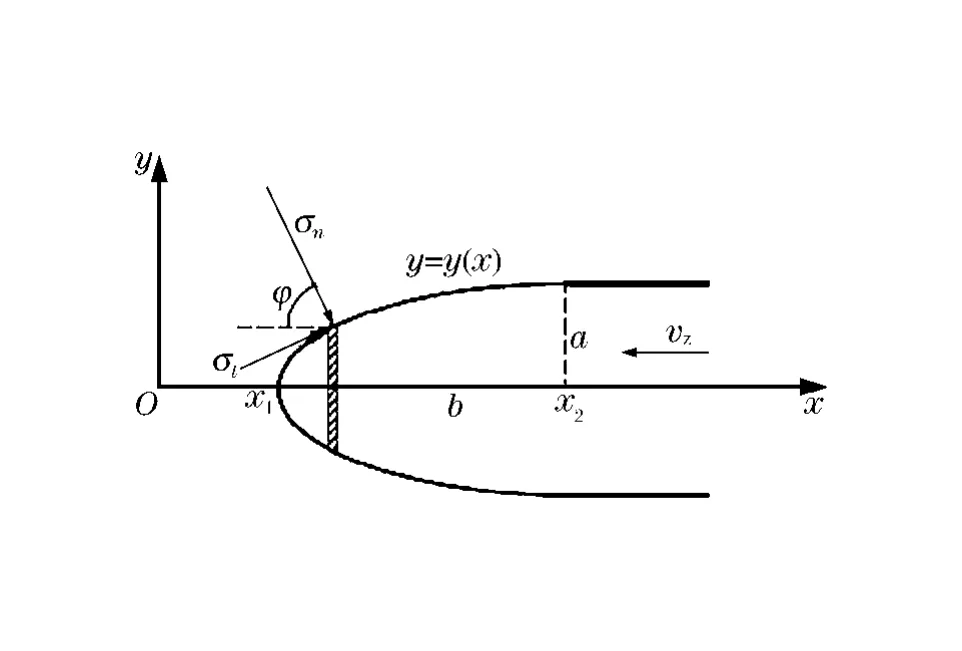
图2 任意头部形状弹体的受力分析Fig.2 Force analysis for any nose profile

弹体倾角侵彻／攻角侵彻靶板的问题中，弹体轴线与靶板表面法线夹角带来的横向载荷对弹体结构的影响十分显著。横向载荷在弹体内会产生剪切力与弯矩，因此为保证在侵彻过程中弹体结构不发生塑性弯曲，对于以一定初速度斜侵彻靶板的弹体存在最大理论着角［18］。斜侵彻弹体横向载荷随初速度的增加而增大，相应最大理论着角随弹体初速度增加而减小。当弹体以很高的初速度撞击靶板时，对着角的要求就十分苛刻。实验中发射的弹体，由于脱壳、气动等因素的影响，很难有完全理想状态的垂直着靶姿态，因此正侵彻靶板的弹体通常都带有微小的攻角βa。根据文献［5-11］，弹体正侵彻时均带有微小攻角，绝大部分实验微小攻角的变化范围为0°≤βa≤1.0°。因此对于高速侵彻弹体，微小攻角产生的横向载荷可能对弹体结构造成严重的影响，出现高速侵彻弹体弹身弯曲的现象。

3.1 问题的简化

侵彻过程中弹体的过载加速度测试结果［10－11］与弹体的受力分析［5，17］表明，弹体侵彻混凝土靶板所受阻力的最大值出现在开坑阶段结束和孔道阶段开始的时刻t1，即

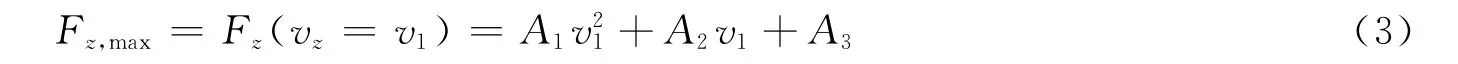
此刻弹体头部尖端距离靶板表面为开坑深度4a，头部完全嵌入靶板内。如图3所示，若弹体着靶前带有小攻角βa，设其变化范围为0～1.0°，可以近似认为由弹体头部产生的侵彻阻力与垂直侵彻条件下相等。将弹体头部产生的侵彻阻力依据材料力学中对于轴向内力的分析方法等效作用于弹身部分，引入除弹体头部质量的等效参数k，将该参数定义为k＝mb／m，其中mb是弹身部分的质量，m是弹体总质量。则等效后的阻力按正交分解方法简化分解为作用于弹身部分的最大横向与轴向载荷

弹体受力如图3所示，等效后的轴向与横向载荷作用于弹体的圆柱（圆筒）弹身部分，将弹身简化为一个一端受横向与轴向载荷的自由梁（质量为mb），直径和长度与弹身部分相等。图4为卵形头部弹体的结构示意图。简化所得自由梁的直径为d，长度为Ls，如图5所示。忽略侵彻过程中的弹体自身重力作用，按图5中的受力情况，利用梁的平衡方程，对弹身所受载荷进行分析。

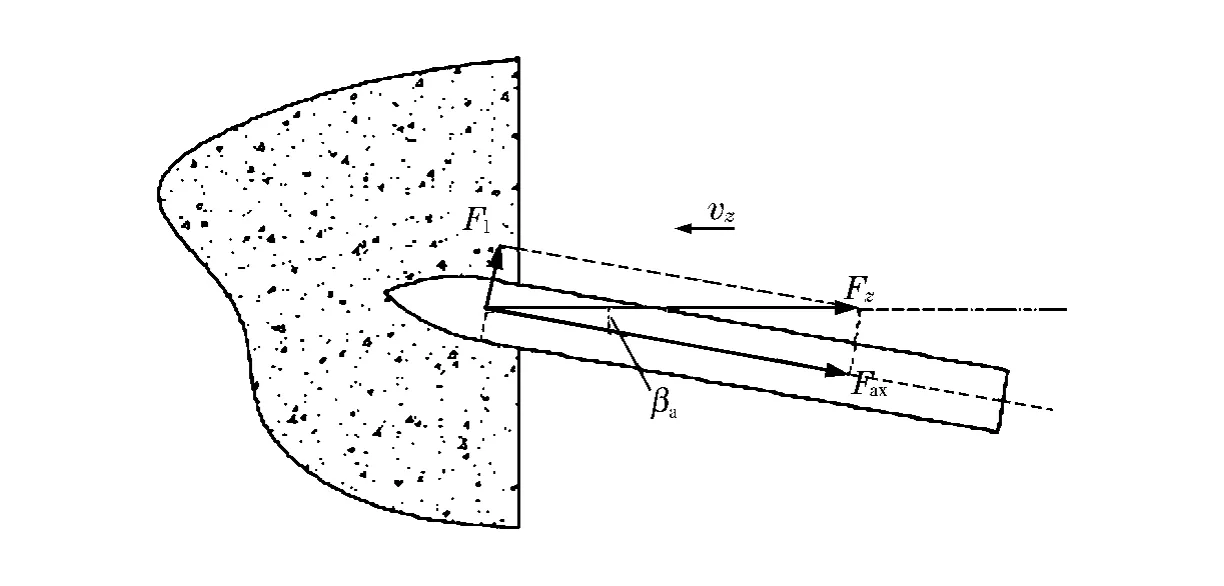
图3 带有小攻角的弹体侵彻示意图Fig.3 Penetration with small angle of attack

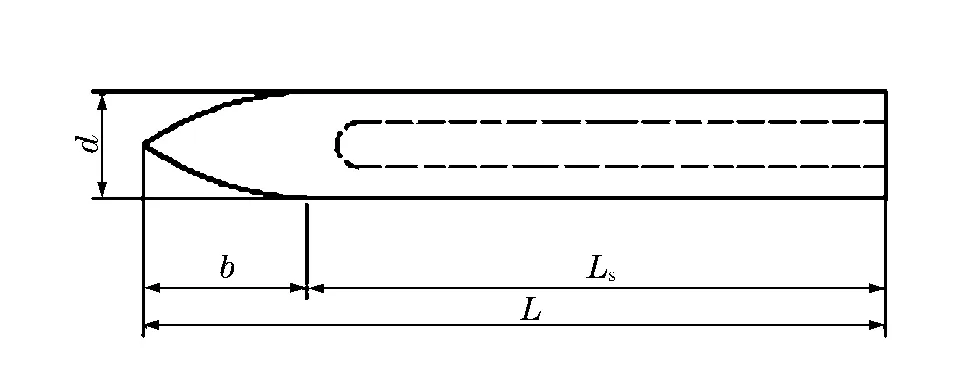
图4 弹体结构示意图Fig.4 Projectile geometry

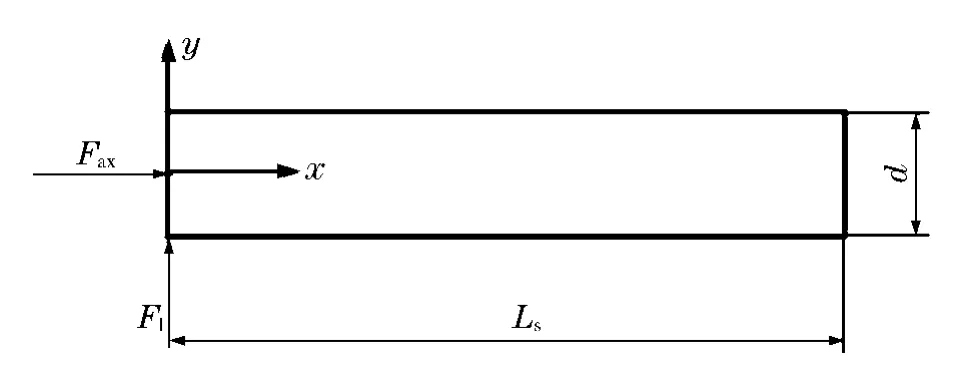
图5 弹体简化后的自由梁Fig.5 Free-free beam simplified from projectile

3.2 载荷分析

3.2.1 轴向载荷

梁的轴向载荷分析相对简单，取x位置截面左侧的部分，由x方向受力平衡和牛顿定律可得

式中：Fax／mb是弹体的加速度，Fx是轴向载荷分布函数，则有

从式（6）可以看出梁的轴向载荷随着x增加而线性递减，其中左端（x＝0）所受的轴向载荷最大，与等效载荷Fax相等。轴向载荷主要使弹体作减速运动，几乎不对弹体结构造成影响。

3.2.2 横向载荷

横向载荷会在梁中产生剪切力与弯矩，对结构影响显著。在梁弯曲的平截面假设的基础上，进行梁的横向载荷分析。已知梁的横向运动平衡方程为

式中：Q表示梁的剪切力，Y表示梁的横向位移，m′b是梁的线质量。设梁的质心位于其几何中心，则梁的横向运动加速度与旋转角加速度分别为

由式（8）可以得到梁任意位置x处的横向加速度为

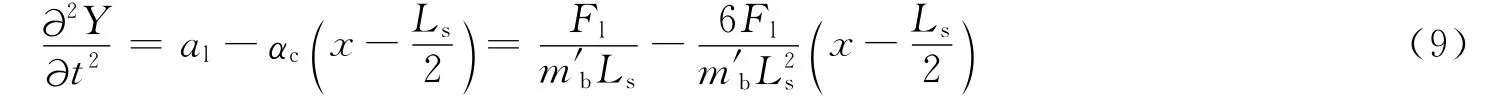
将式（9）代入平衡方程（7），结合梁右端剪切力为零的边界条件可得微分方程

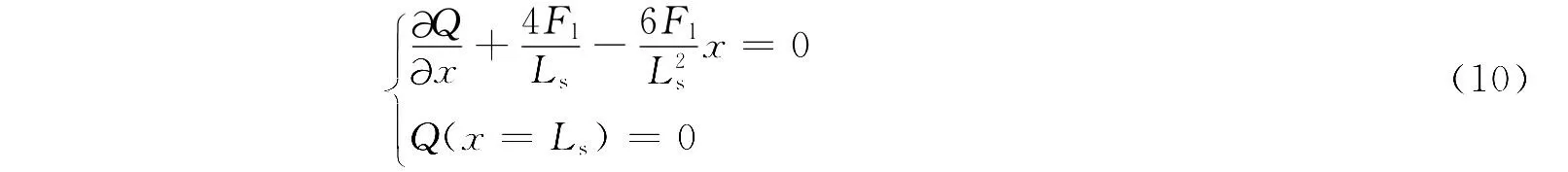
求解后可获得梁的剪切力函数为

已知梁弯曲的剪切力Q与弯矩M 有如下关系，同时结合右端弯矩为零的边界条件有

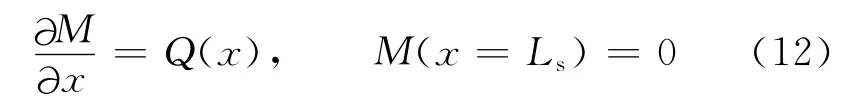
求解上述微分方程后得到梁的弯矩函数为

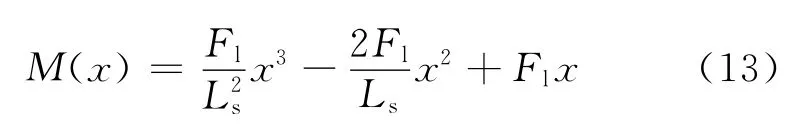
根据式（12）和极值原理，可以求得当剪切力Q＝0时，x＝Ls／3处是梁中弯矩最大的位置，该最大弯矩

将式（11）和（13）进行量纲一化得到梁的量纲一剪力和弯矩函数

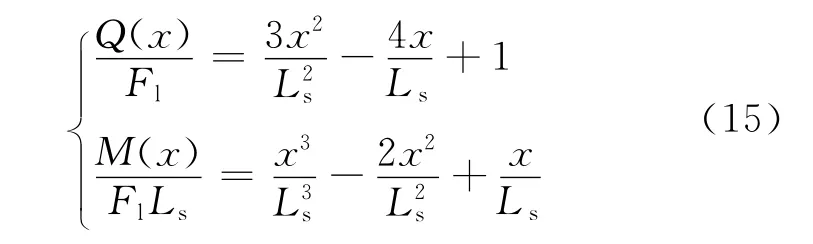
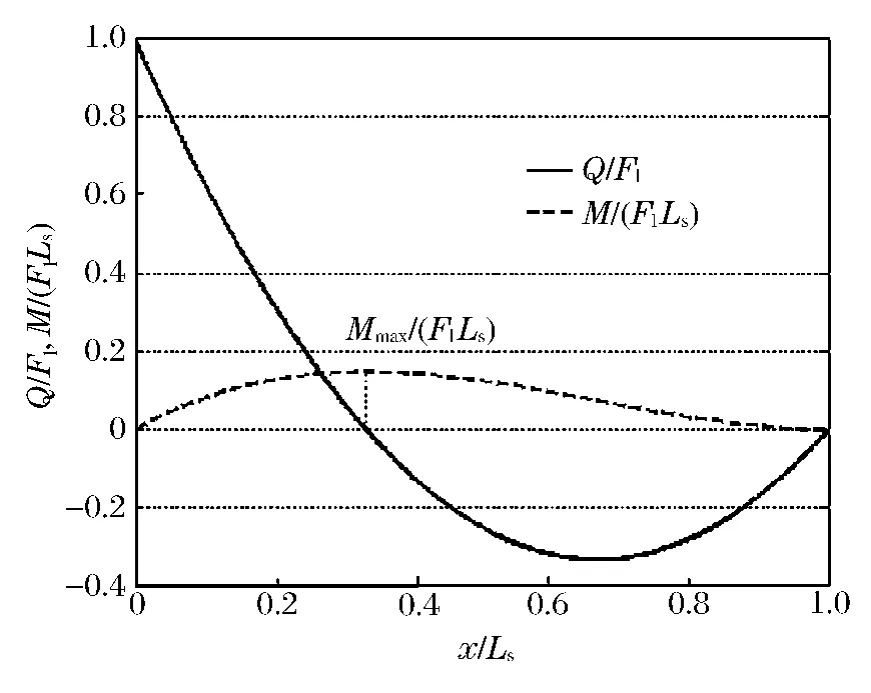
图6 梁的量纲一剪切力与弯矩分布Fig.6 Dimensionless shear force and bending moment of beam

图6为梁的量纲一剪切力与弯矩分布图。

3.3 弹体发生弯曲的临界条件

由弹体简化梁的剪切力与弯矩分布可以进行弹体的抗弯性分析。在梁弯曲的平截面假设基础上进行弯曲应力分析，可得横向载荷下梁所能承受的最大弯矩

式中：σs表示弹体材料的屈服强度，W 是梁的抗弯截面系数。对于实心弹体和空心弹体，其圆形截面和圆环截面的抗弯截面系数分别为

式中：Iz是梁截面对其中性轴的惯性矩，di表示空心弹体内径。

当弹体的最大弯矩达到或超过所能承受的弯矩时，弹体发生塑性弯曲。令式（14）与（16）相等，就得到了弹体发生弯曲的理论临界条件

对式（18）进一步变形可得

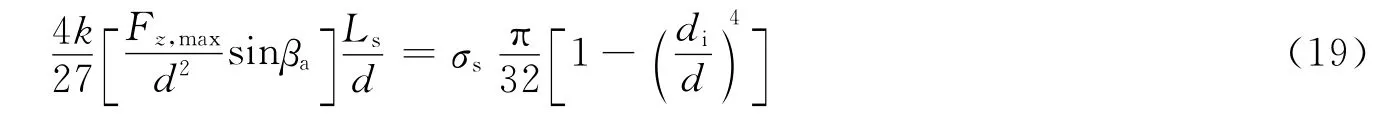
若式（19）中di＝0表示弹体为实心，由式（3）可得

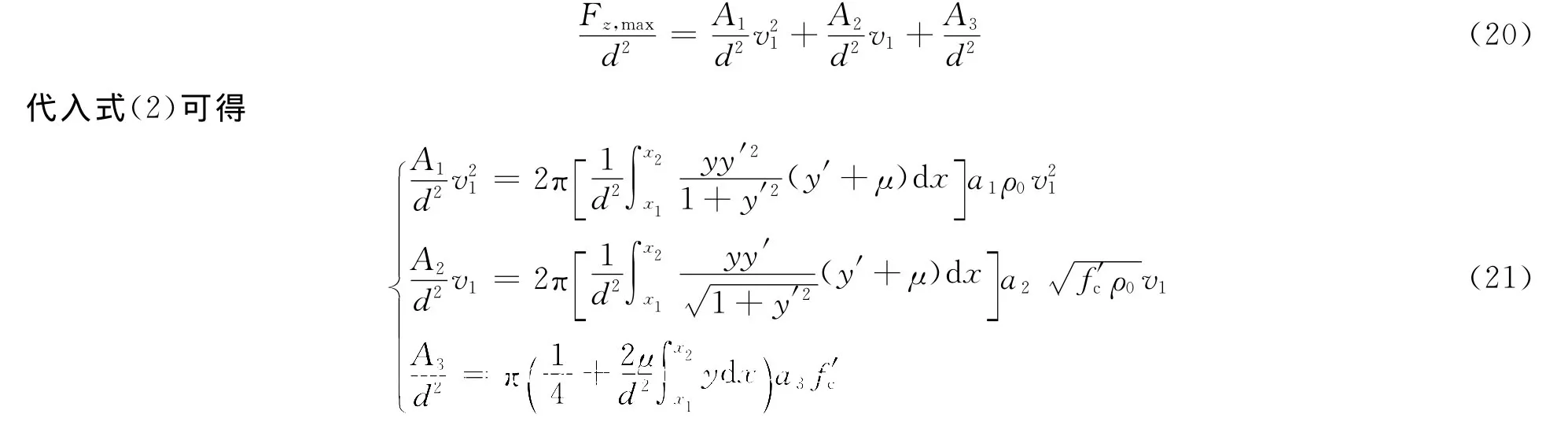
通过量纲分析和文献［12］可知，式（21）中的积分均表示弹体头部受力的量纲一数，因此Fz，max／d2与弹体直径无关，量纲等同于式（19）右侧的弹体材料强度σs；而式（19）中的其他项均为量纲一数，由此说明弹体发生弯曲的理论临界条件具有几何相似性。因此，控制弹体弯曲的主要特征分为3个方面：（1）弹体着靶前的状态：弹体初速度决定的侵彻阻力和弹体带有的小攻角；（2）弹体的结构：弹体长径比与截面形状；（3）弹体材料的强度。因此可以从弹体着靶前状态和弹体结构两方面对理论弯曲条件下的弹体材料强度要求进行计算，以得到在弹体弯曲条件下，这些特征之间的关系。

在弹体结构确定（Ls、W 为常数）的情况下，弹体发生弯曲的理论临界条件主要受3个量控制：弹体所受阻力Fz，小攻角βa，弹体材料屈服强度σs。由刚性弹体侵彻混凝土的研究［5，13］可知，在混凝土靶板性能和弹体头部形状不变的情况下，弹体所受阻力仅与弹体初速度相关。因此下面通过计算分析弹体初速度、小攻角及弹体材料强度这3个特征量在弹体弯曲理论临界条件下的关系。计算用弹体参数为：L＝300mm，d＝30mm，di＝14mm，Ws＝2 650.7mm3，Wh＝214.5mm3；混凝土靶板的参数为：＝48MPa，ρ0＝2.3t／m3，ν＝0.2。

图7为理论弯曲临界条件式（19）中小攻角、弹体初速度和弹体材料强度之间的依赖关系，其中0.1°≤βa≤1.0°，400m／s≤vs≤1.6km／s。从图中可以看出小攻角与弹体初速度对弹体材料强度要求的影响趋势。随着小攻角βa和弹体初速度vs增大，对弹体材料的强度要求显著增强。由于实心与空心弹体的抗弯截面系数相差一个数量级，图7（a）与图7（b）的计算结果相比，对弹体材料强度的要求也相差一个数量级，表明空心弹体高速撞击靶板对弹体材料的强度要求更高。高强度钢质材料（σs≥1GPa）实心弹体在图示初速度和攻角范围内撞击靶板，理论上不会发生塑性弯曲；而相同条件下空心弹体对其材料强度的要求已经达到吉帕量级，表明弹体的弯曲成为可能。若弹体着靶前的条件位于图中曲面下方，则表示会引起弹身弯曲。所以对于高强度材料制成的空心侵彻弹体，在很高速度碰撞靶板条件下，也极易发生弹体的塑性弯曲。

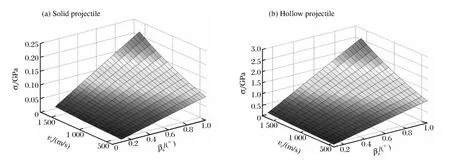
图7 理论弯曲临界条件中小攻角、弹体初速度和弹体材料强度间的关系Fig.7 Dependence of small angle of attack，impact velocity and yield strength of projectile based on theoretical bending condition

设弹体着靶前的状态确定，弹体的初速度vs＝1km／s，小攻角为βa＝1.0°，计算弹体结构对弹体弯曲的影响。弹体结构参数有弹体长度L和弹体的内外直径di、d。为了使分析结果更具一般性，计算弹体长径比与内外径比对弹体材料强度的要求。图8为弹体的长径比、弹体内外径比和弹体材料强度间的依赖关系。弹体的内外径比为0～0.6，表示弹体从实心到空心的过渡，可以看出内外径比在超过一定数值后，对弹体材料强度要求影响十分显著；弹体长径比对材料强度要求的影响呈线性递增趋势，且增幅随弹体的内外径比增加而增大。所以在侵彻弹体的设计中，除了增加长径比以增强弹体侵彻能力以外，需要在产生最大弯矩的位置增加弹体壁厚以增加其抗弯刚度，保证弹体侵彻时的结构不受破坏，同时弹体内部的填充物也会增加一定的抗弯性。

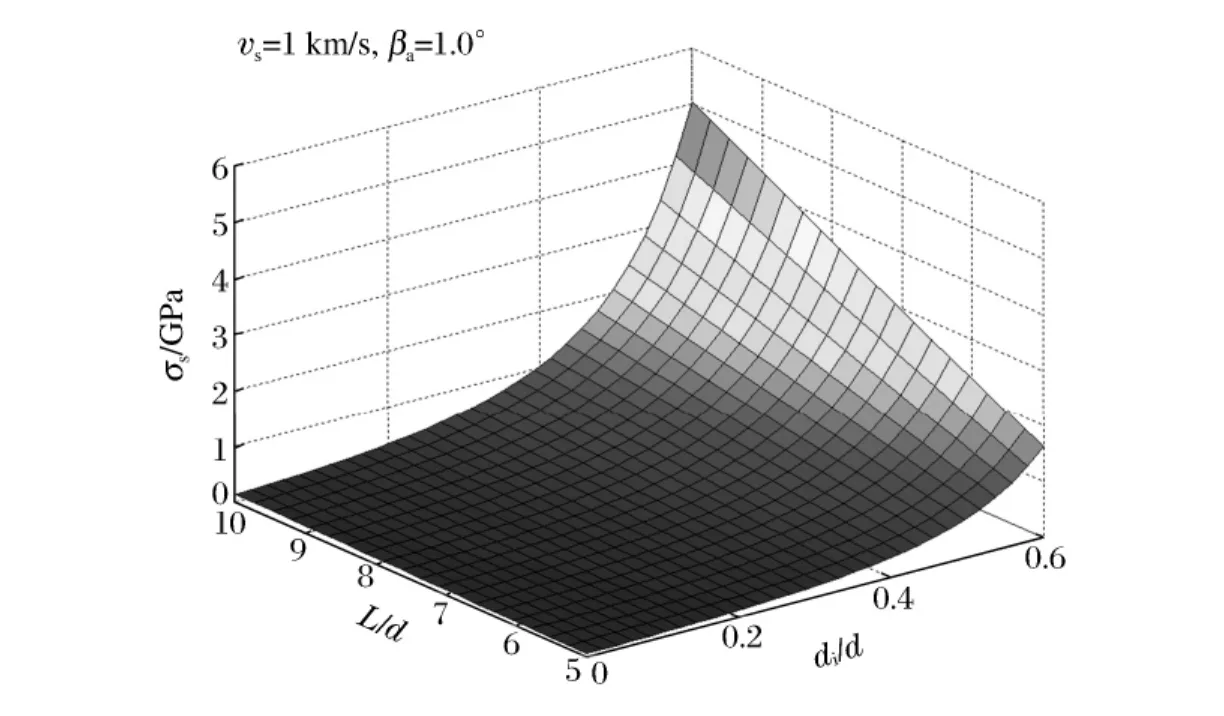
图8 理论弯曲临界条件中弹体内外径比、长径比和弹体材料强度间的关系Fig.8 Dependence of cartridge ratio，length-diameter ratio and yield strength of projectile based on theoretical bending condition

4 实验中的弹体弯曲

由上文分析已知弹体的弯曲条件具有几何相似性，所以用缩比弹体实验模拟真实弹体侵彻过程出现的弯曲是有效的。在弹体初速度为400～1 500m／s的正侵彻混凝土靶板实验中，随着弹体初速的增大，出现了弹身弯曲的现象，使弹体失去侵彻能力。本节中将上述理论分析结果与实验中记录的弹体弯曲结果进行对比，以验证理论分析的正确性。

图9为实验弹体结构图，弹体头部采用CRH＝3.0的卵形头部，长径比L／d＝7，弹体尾部带有一定锥度。实验弹体采用不同强度材料制成，弹体材料与混凝土靶板详细参数见表1，表中δs为伸长率。

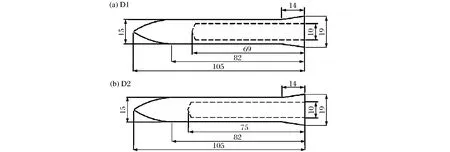
图9 实验弹体结构图Fig.9 Experiment projectile geometry

表1 实验弹体与混凝土靶板参数Table 1 Parameters of experiment projectile and concrete target

表1中D1结构弹体使用超高强度材料制成，而D2结构的弹体使用屈服强度较低的材料。从式（18）可知，低强度材料弹体初速度较低就会发生弹体弯曲现象，这一点与实验观测相吻合。图10为侵彻实验中发生弯曲或断裂的回收弹体照片，可以看出弹身部分出现严重弯曲甚至断裂。由于D1结构弹体壁厚薄，作为弹体材料的30CrMnSiNi2A伸长率较低，图中D1结构30CrMnSiNi2A材料弹体均发生断裂。已知弹体的断裂是由弯曲引起的，但由于本文中是研究弹体发生弯曲的临界条件，因此对弹体弯曲与断裂的关系在本文中不做进一步分析。图中弹体发生弯曲或断裂的位置相同，基本都位于距离头部结束点的三分之一弹身长处，与理论分析中最大弯矩产生的位置一致，如图11所示。

图10 弯曲或断裂弹体的回收照片Fig.10 Post-test photographs of bent and fractured projectiles

图11 实验弹体发生弯曲的位置Fig.11 Bending position of experiment projectile

对弹体着靶前飞行姿态高速摄影照片（图12）进行测量，可以得到发生弯曲和断裂的弹体在垂直平面内的小攻角。测绘得到的小攻角记录于表2中。

图12 弹体飞行姿态高速摄影照片Fig.12 High-speed photographys of projectiles in flight

表2 实验弹体飞行垂直平面内的小攻角Table 2 Small angle of attack of projectile in vertical plane

图13为弹体发生弯曲条件下的弹体初速度与弹体材料屈服强度关系。图中的数据点表示实验中弹体出现弯曲或断裂。根据表2中记录的攻角情况，考虑水平面内可能的攻角大小，取βa＝0.3°代入式（18），在实验弹体结构条件下计算弹体初速度与材料屈服强度的关系，得到图13中的曲线。从图13可以看出，结构D1与D2的弹体壁厚不同，使相同攻角（βa＝0.3°）下的计算结果产生如图所示2条曲线的差异。虽然测量所得的弹体小攻角不是很精确，且实验数据具有离散性，但图中不同结构和材料弹体的实验数据点与计算曲线相邻，表明式（18）的理论弯曲临界条件基本符合实际情况，可以为侵彻弹体的结构与强度设计提供参考。

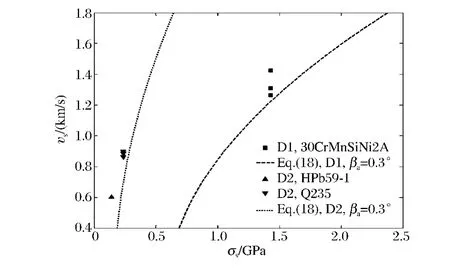
图13 弯曲临界条件下弹体初速度与材料屈服强度的关系Fig.13 Relation of impact velocity and yield strength under bending condition

5 结 论

通过将弹体简化为受轴向与横向载荷的自由梁，获得了弹体的载荷分布与最大弯矩。与梁的弯曲应力分析相结合，推导出弹体弯曲的理论临界条件，该条件具有几何相似性，且主要受3个特征控制：弹体着靶前的状态、弹体的结构以及弹体材料的屈服强度。计算得到了弹体的初速度和小攻角，长径比和内外径比与弹体材料强度之间的关系，从理论上证实了高强度材料空心结构弹体高速侵彻混凝土靶板时发生弹体弯曲的可能性。本文工作可为高速侵彻弹的设计研制提供理论支持。

［1］Forrestal M J.Penetration into dry porous rock［J］.International Journal of Solids and Structures，1986，22（12）：1485-1500.

［2］Luk V K，Forrestal M J.Penetration into semi-infinite reinforced-concrete targets with spherical and ogival-nose projectiles［J］.International Journal of Impact Engineering，1987，6（4）：291-301.

［3］Luk V K，Forrestal M J.Comment on“Penetration into semi-infinite reinforced-concrete targets with spherical and ogival-nose projectiles”［J］.International Journal of Impact Engineering，1989，8（1）：83-84.

［4］Forrestal M J，Luk V K.Penetration into soil targets［J］.International Journal of Impact Engineering，1992，12（3）：427-444.

［5］Forrestal M J，Altman B S，Cargile J D，et al.An empirical equation for penetration depth of ogive-nose projectiles into concrete targets［J］.International Journal of Impact Engineering，1992，15（4）：395-405.

［6］Forrestal M J，Frew D J，Hanchak S J，et al.Penetration of grout and concrete targets with ogive-nose steel projectiles［J］.International Journal of Impact Engineering，1996，18（5）：465-476.

［7］Frew D J，Hanchak S J，Green M L，et al.Penetration of concrete targets with ogive-nose steel rods［J］.International Journal of Impact Engineering，1997，21（6）：489-497.

［8］Frew D J，Forrestal M J，Hanchak S J.Penetration experiments with limestone targets and ogive-nose steel projectiles［J］.Journal of Applied Mechanics（Transactions of the ASME），2000，67（4）：841-845.

［9］Forrestal M J，Hanchak S J.Penetration limit velocity for ogive-nose projectiles and limestone targets［J］.Journal of Applied Mechanics（Transactions of the ASME），2002，69（6）：853-854.

［10］Forrestal M J，Frew D J，Hickerson J P，et al.Penetration of concrete targets with deceleration-time measurements［J］.International Journal of Impact Engineering，2003，28（5）：479-497.

［11］Frew D J，Forrestal M J，Cargile J D.The effect of concrete target diameter on projectile deceleration and penetra-tion［J］.International Journal of Impact Engineering，2006，32（10）：1584-1594.

［12］Chen X W，Li Q M.Deep penetration of a non-deformable projectile with different geometrical characteristics［J］.International Journal of Impact Engineering，2002，27（6）：619-637.

［13］Li Q M，Chen X W.Dimensionless formulae for penetration depth of concrete target impacted by a non-deformable projectile［J］.International Journal of Impact Engineering，2003，28（1）：93-116.

［14］Li Q M，Weng H J，Chen X W.A modified model for the penetration into moderately thick plates by a rigid，sharp-nosed projectile［J］.International Journal of Impact Engineering，2004，30（2）：193-204.

［15］Chen X W，Fan S C，Li Q M.Oblique and normal perforation of concrete targets by a rigid projectile［J］.International Journal of Impact Engineering，2004，30（6）：617-637.

［16］Lundgren R G.High velocity penetrators［R］.SAND94-2724C，Conf-9411142-1，1994.

［17］Wang Y N，Wu H J，Huang F L，et al.Analysis of rigid motion for penetration of concrete［C］∥Proceedings of the 7th international conference on shock ＆impact loads on structures.Singapore：CI-PREMIER PTE LTD，2007：627-638.

［18］陈小伟.动能深侵彻弹的力学设计（I）：侵彻／穿甲理论和弹体壁厚分析［J］.爆炸与冲击，2005，25（6）：499-505.

CHEN Xiao-wei.Mechanics of structural design of EPW （Ⅰ）：The penetration／perforation theory and the analysis on the cartridge of projectile［J］.Explosion and Shock Waves，2005，25（6）：499-505.

Bending of projectile with small angle of attack during high-speed penetration of concrete targets＊

WANG Yi-nan，HUANG Feng-lei，DUAN Zhuo-ping
（State Key Laboratory of Explosion Science and Technology，Beijing Institute of Technology，Beijing100081，China）

The bending of the projectile in the process of high-speed penetrating concrete is studied by simplifying the projectile as a free-free beam.The bending moment caused by the transverse load which is generated from small angle of attack and penetration resistance is analyzed through theoretical work.The analysis showed that the theoretical bending condition is dominated by initial status，structure and material of the projectile.The computed results proved that the bending of high-speed penetrating projectile is affected by the existence of small angle of attack.The penetration experiment also indicates that the bending position and the bending condition obtained from experiment results are well agreed with theoretical analysis.

mechanics of explosion；bending of projectile；high-speed penetration；kinetic energy pen-etrator；concrete target

17July 2009；Revised 17November 2009

HUANG Feng-lei，huangfl＠bit.edu.cn

（责任编辑 曾月蓉）

O385 国标学科代码：130·35

A

1001-1455（2010）06-0598-09

2009-07-17；

2009-11-17

爆炸科学与技术国家重点实验室自主研究课题项目（ZDKT08-04）

王一楠（1983— ），男，博士研究生。