柱形罐爆炸碎片抛射的MonteCarlo分析*-

刘振翼，黄 平，徐亚博

（北京理工大学爆炸科学与技术国家重点实验室，北京 100081）

柱形罐爆炸碎片抛射的MonteCarlo分析*-

刘振翼，黄 平，徐亚博

（北京理工大学爆炸科学与技术国家重点实验室，北京 100081）

在动力学分析的基础上，将二维体系内的碎片轨迹方程扩展到三维体系内，将风这一影响因素考虑在内。以墨西哥事故中水平圆柱储罐发生沸腾液体扩展为蒸气云爆炸（BLEVE）为例，利用Monte-Carlo法模拟出碎片的轨迹曲线，计算得到有风和无风情况下碎片抛射距离的概率分布，得到一般情况下风对碎片危害的影响较小。计算了无风情况下碎片碰撞目标容器的概率，得到碰撞概率随罐间距的增大而呈现严格的指数衰减趋势，通过此关系式可以计算出符合安全要求的罐间距。研究结果对于提高储罐的安全性、缓解和控制碎片产生的风险具有一定的指导意义。

爆炸力学；沸腾液体扩展为蒸气云爆炸；Monte-Carlo法；碎片；柱形罐

1 引 言

危险设施由于装载过量、腐蚀及火灾等原因产生的爆炸除了产生冲击波，一部分能量还会转化为碎片的动能。这种具有动能的碎片在飞行过程中有可能造成人员伤亡或目标设备的损坏，进而造成更大的灾难事故，这种现象被称为多米诺效应或连锁效应。由于多米诺事故的严重性，欧盟的塞维索法令II对重大危险源的多米诺效应做出专门规定，要求重大危险源企业提交的安全报告中要有多米诺效应分析的内容，可能产生多米诺效应的企业之间要共享信息等［1－5］。火灾热辐射、爆炸冲击波和碎片是造成多米诺效应的主要原因，本文中将研究碎片造成多米诺事故这部分内容。荷兰的应用技术研究院和美国的化学工艺安全中心给出了碎片抛射距离的经验计算公式。U.Hauptmanns［6－7］通过对事故碎片的随机和不确定性进行分析，利用Monte-Carlo方法得到爆炸碎片到达不同距离的概率曲线。G.Cozzani等［8］在U.Hauptmanns的基础上，考虑目标的影响，得到爆炸碎片碰撞目标容器的概率。文献［9-11］采用类似文献［7-8］的方法来计算碎片的抛射范围。

本文中，将在前人研究的基础上，考虑风向和风速，将目前通用的二维体系内的碎片轨迹方程扩展到三维体系内，利用Monte-Carlo法得到柱形罐爆炸碎片在有风和无风情况下到达不同距离的概率曲线，及撞击不同距离处的目标容器的概率，并对2种情况下的计算结果进行比较分析。

2 三维体系内碎片轨迹方程

将事故源、碎片和目标放入三维体系中分析，如图1所示。由于碎片与目标相比通常较小，为简化计算，忽略不计碎片的大小。由于碎片主要绕着质心运动，因此可用质心的轨迹和速度来代表整个碎片的轨迹和速度。参考系O-xyz的原点O为碎片质心的初始位置（即事故源），其中xOy与地面平行，z轴与重力方向相反。向量vp代表碎片的初速方向，与xOy平面的夹角为φ，在xOy平面上的投影与x轴的夹角为θ。向量vw代表风向，与x轴的夹角为φ，在此仅考虑与xOy面平行的风。

碎片在飞行过程中受重力、阻力和升力的联合作用。由于引入升力会造成计算过于复杂，且升力只适用于端盖，当升力方向与端盖轨迹的夹角超过10°时，升力可忽略不计，因此在实际计算中，为了简化，升力不计在内［7］。根据牛顿第二定律得到

式中：D是阻力，g是重力加速度，ap是碎片的加速度，mp是碎片的质量。

对于空气阻力的作用，Lees分析了3种情况：没有阻力；阻力与碎片速度成正比；阻力与碎片速度的平方成正比。认为在亚音速范围内，阻力与碎片速度的平方成正比这种情况是最合理的［10，12］。若考虑风的影响，此时的速度应为相对速度，即碎片速度与风速之差，因此阻力的计算公式为

式中：ρa是空气密度，CD是空气阻尼系数，AD是迎风面积，vre是碎片与风的相对速度，kD是阻力系数。

在xOy平面内仅存在阻力对碎片的影响，在竖直方向则要考虑阻力和重力的双重影响，因此将式（1）扩展，得到三维体系内碎片的加速度方程为

式中：x、y是水平方向坐标，z是竖直方向坐标，t是碎片飞行时间，vw是水平方向恒定风速。碎片在下降阶段n＝1，在上升阶段n＝2。

参考图1，给出式（4）～（6）的初始条件，x、y和z方向的初速度和位置分别为

式中：v0是碎片的初速度。

将初始条件（7）～（9）代入方程（4）～（6），利用 MATLAB求解得到

x方向

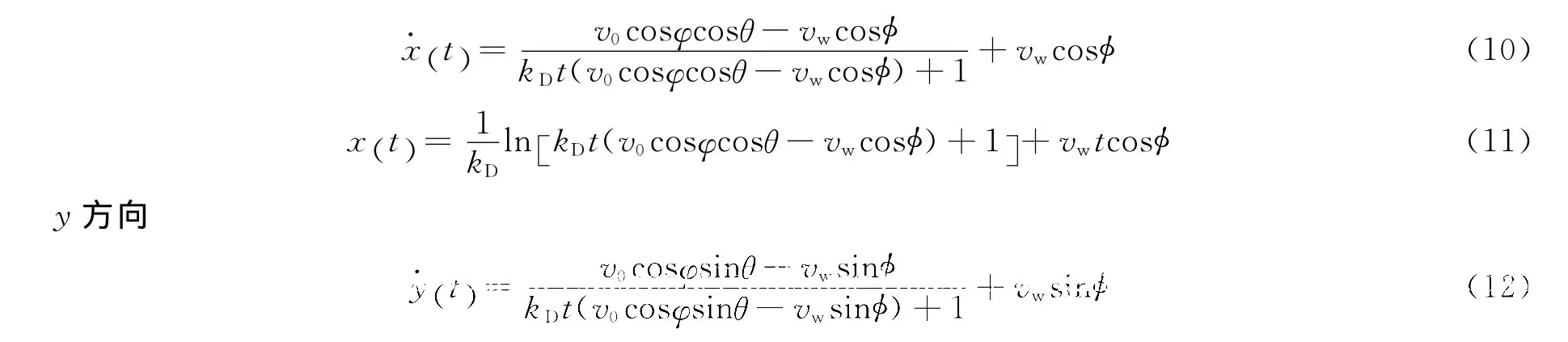
3 不确定参数的确定

3.1 碎片初始速度

碎片的初速度

式中：Ek为碎片的初动能，mp为碎片的质量。

要计算碎片的动能，需要计算储罐爆炸时释放的能量E。目前有很多模型可用来计算气体储罐和过热液体储罐能量，本文中采用 Baum 模型［6，7，13］

式中：V为储罐体积，p1为储罐爆炸时的压强，p0为大气压，γ为比热容。

储罐爆炸压强p1取决于爆炸情况：（1）超压情况下，爆炸压强为最大工作压强×安全系数；（2）物理爆炸情况下，爆炸压强为正常的操作压强；（3）火灾情况下，爆炸压强等于泄压压强的1.21倍［13］。由于在实际情况下很难确定储罐爆炸时的真实压强，所以储罐爆炸压强被当作是随机变量，通常认为其在上述数值的90%～110%之间，且服从均匀分布［6，7］，数学表达式为

式中：p是计算中使用的容器爆炸压强，Pa；εrand是［0，1］区间上的随机数。

由于储罐爆炸时，还要产生爆炸冲击波、撕碎工艺设施等，只有部分能量转化为碎片的能量，因此，碎片的初动能［13］

式中：fk为动能比例因子，其值服从［0.2，0.5］的右三角分布，且均值为0.3，数学表达式为

3.2 碎片的数量、质量、形状、能量和抛射角

对46次相关事故的分析表明，柱形罐爆炸产生的碎片数量N服从对数正态分布，其均值为0.855 16，标准差为0.524 48［7，14－16］，数学表达式为

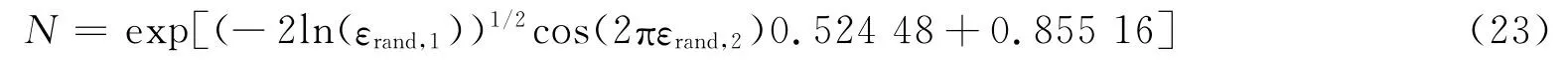
式中：εrand，1、εrand，2是［0，1］区间上的2个相互独立的随机数。

根据P.L.Holden等［14］的结论，碎片质量占总质量的比例服从贝塔分布，且参数a＝0.412 13，b＝1.392 6。贝塔分布的概率密度函数为

式中：x为［0，1］区间上的随机变量。

柱形罐爆炸可产生端盖和弹片2种碎片形式。由于很难精确确定端盖和碎片的比例，一般采用20%的端盖和80%的弹片［7］。

假设加载在每个端盖上的能量相等，加载在第i个弹片上的能量占总动能的比例［7］

式中：I是总弹片数量；mi是第i个弹片的质量。

端盖和弹片的水平角θ均服从均匀分布［7，14－15］，如图2所示。其中

20%在［30°，150°］内，数学表达式为

30%在［150°，210°］内，数学表达式为

20%在［210°，330°］内，数学表达式为

30%在［330°，30°］内，数学表达式为

图2 柱形罐爆炸碎片的水平角分布Fig.2 Horizontal angle distribution of fragment from cylindrical vessel explosion

端盖的垂直角φ服从［0°，10°］内的均匀分布，数学表达式为

弹片的垂直角φ服从［0°，90°］内的均匀分布，数学表达式为

3.3 阻力系数

碎片抛射阻力系数取决于碎片的几何形状、表面粗糙度和碎片与抛射方向的夹角，其数值一般在2.9×10－4～2.1×10－3之间。由于阻力系数较难确定，R.Pula等［17］采用5种阻力系数，分别为0，2.9×10－4，6.0×10－4，1.21×10－3和2.0×10－3，计算出5种阻力水平下碎片飞行时间对应的飞行高度及不同初始速度对应的抛射距离，得到抛射距离随阻力系数的增加而减小，且当初速度小于35m／s时，阻力作用在碎片抛射距离上的作用非常小，几乎可以忽略不计。2.9×10－4和6.0×10－4这2种情况对应的阻力系数较小，接近无阻力，而2.0×10－3适用于超音速的范围。由于爆炸碎片一般在低音速范围内（200m／s左右），因此建议采用1.21×10－3作为阻力系数。本文中阻力系数均采用1.21×10－3。

3.4 储罐充装水平

储罐爆炸能量主要来自2部分：储罐上方的蒸气膨胀和储罐下方的液体汽化膨胀（蒸气爆炸）。由于前者在储罐内只占很小的一部分，计算时可忽略不计。

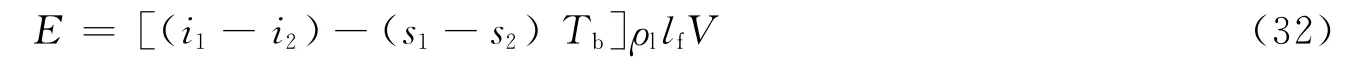
液化石油气汽化膨胀爆炸的能量［10］式中：i1是液化石油气在储罐破裂时的压力或温度下的焓，i2是液化石油气在大气压下的焓，s1是液化石油气在储罐破裂时的压力或温度下的熵，s2是液化石油气在大气压下的熵，Tb是液化石油气在大气压下的沸点，ρl是液化石油气密度，lf是充装水平；V是储罐容积。

由式（32）看出，充装水平lf直接影响储罐的爆炸能量。lf越高，储罐爆炸能量越大，碎片的抛射距离也就越远，反之，lf越低，爆炸能量越小，抛射距离也就越近。一般假设lf在0.1～0.8倍储罐总容量的范围内，且均匀分布［8－9］，数学表达式为

4 Monte-Carlo法计算抛射碎片碰撞目标的概率

在储罐爆炸事故中，计算抛射碎片碰撞目标的概率，需要考虑以下参数：爆炸时储罐压力、储罐爆炸能量、装载程度、初始能量转化为碎片能量的比例、碎片数目、碎片形状和质量、碎片抛射角、阻力系数、风速和风向等因素，这些参数都是随机变量，具有一定的不确定性，具体数值在一定的区间范围内。由于参数存在不确定性，在实际计算中，若用常规的点估计很难得到一个可信的结果，而Monte-Carlo法采用大量的抽样对随机变量和不确定性进行模拟，可以解决参数的不确定性问题。

为了简化计算，分析中忽略目标的形状，认为只要碎片落在目标的外切立方形区域即算撞击到目标，这种假设正好可弥补一部分因忽略碎片大小而产生的误差。当参数和目标数据已知后，用Monte－Carlo方法进行数值模拟，将这些参数代入碎片轨迹方程，计算出碎片从抛射到落地间的轨迹曲线，当轨迹与目标的外切立方体有交集时，n取1，当无交集时，n取0。用此方法，模拟Nsim次即可得到碰撞概率Pimp，计算公式为

式中：Nsum为1次模拟中产生的碎片数目；Vtar为目标的外切立方形区域；Vfrag为碎片的抛射轨迹；Nsim为模拟次数。

5 案例分析

以墨西哥城BLEVE事故中盛装丙烷的水平柱形罐为案例，模拟计算中所需参数见表1［7］，表中r0、d0、m0、ρ0分别表示柱形罐的半径、厚度、质量和密度。图3～7分别给出了计算和事故数据的比较、模拟的碎片轨迹、有风和无风情况下碎片抛射距离的概率分布、落点分布及无风情况下碎片碰撞目标容器的概率。

表1 柱形罐的参数值或分布Table 1 Cylindrical vessel’s process parameters

图3给出了计算和事故数据之间的比较。可以看出，在当前给定的计算参数下，模拟结果跟实际数据一致性较好。图4是模拟储罐爆炸碎片被抛射的空间分布情况。表明通过Monte-Carlo方法可以清楚地掌握每个碎片的飞行轨迹，为以后计算奠定基础。

图3 计算和事故数据间的比较Fig.3 Comparison between the probabilities of fragment ranges to be reached and calculation

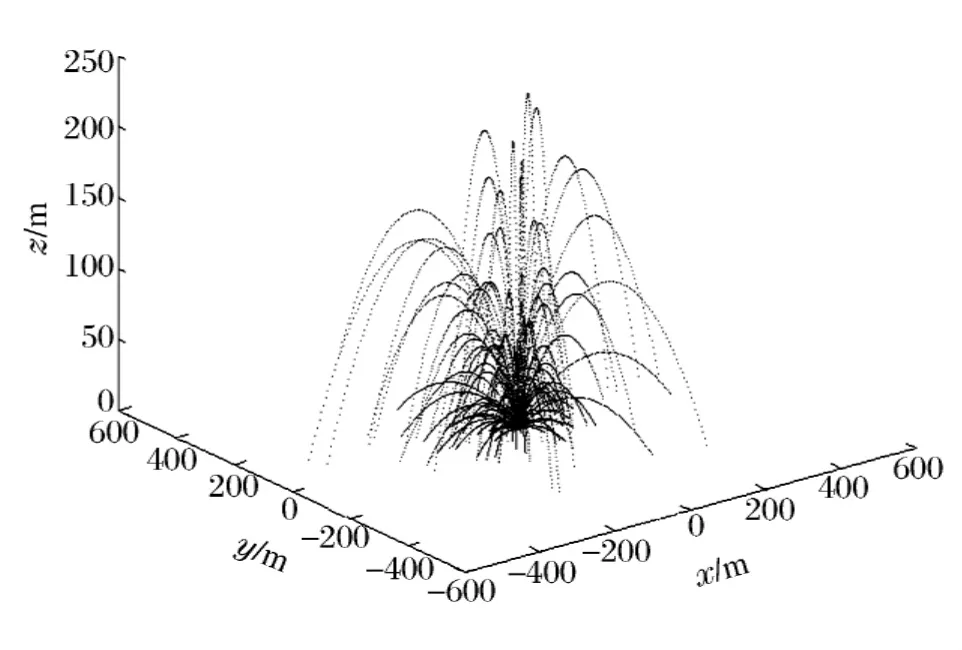
图4 模拟碎片轨迹图Fig.4 Fragment trajectory of simulation

图5是在有风和无风情况下碎片抛射距离的概率分布。为了更有代表性，计算采用了2种风速，即±5m／s和±30m／s。“＋”表示风速与爆炸点O到目标I方向相同，“－”表示风速与爆炸点O到目标I方向相反。由图5可知，当风速为5m／s时，风对碎片抛射距离的影响可忽略不计，是由于风速与碎片速度（200m／s左右）比较相对较小。当风速为30m／s时，对碎片抛射距离的影响比风速为5m／s时大，这表明当风速提高时，风对碎片抛射距离的影响也随之增加。

图5 有风和无风情况下碎片抛射距离的概率分布图Fig.5 Comparison between the probabilities of fragment ranges to be reached with and without wind

图6是柱形罐爆炸碎片的落点分布。从图中可清楚地看出，水平圆柱形容器的轴方向产生的碎片数量相对较多。因此如果目标处在水平圆柱形的［150°，210°］和［330°，360°］这2个区域内具有较大的危险性。在实际工厂布局时应尽量避开这2个区域，而选择在［30°，150°］和［210°，330°］这2个区域内会相对安全。

图7是碎片碰撞一定距离的目标的概率，本文中采用的目标为与初始事故容器一样的水平圆柱形容器。从图中看出，碰撞概率随罐间距的增加而逐渐减小，且碰撞概率Pimp与罐间距R的关系式为：Pimp＝0.035 7e－0.0548R，且相关系数为0.946 7。可以看出，碰撞概率随罐间距的增大而呈现严格的指数衰减趋势。当R＞70m时，Pimp＜10－3，当R＞100m时，Pimp＜10－4。如果将连锁效应控制在10－4以内，则要求R＞100m，此时100m可作为此安全标准下的罐间所需的安全距离。同样，如果将连锁效应控制在10－3以内，则要求R＞70m，此时70m可作为此安全标准下的罐间所需的安全距离。

图7 无风情况下碎片碰撞目标容器的概率图Fig.7 The impact probabilities of fragment on object with no wind

图6 落点分布图Fig.6 Projectile distribution

6 结 论

（1）将二维体系内的碎片轨迹方程扩展到三维体系内，由此可将风速和风向等影响因素考虑在内，并且计算了有风和无风情况下碎片被抛射的距离。通过分析看出，在一般情况下，风对碎片抛射距离的影响较小。

（2）通过模拟得到的碰撞概率与罐间距的关系式，可以计算出符合安全要求的罐间距。这对于提高储罐的安全性，有效缓解和控制碎片产生的风险，具有一定的指导意义。

（3）只对碎片碰撞目标的概率进行了分析，而未考虑目标被碰撞之后的失效概率。为了定量评价由碎片造成的多米诺风险，目标的失效概率是一个非常重要的因素，值得进一步深入的研究。

［1］刘丽，徐亚博，刘振翼.化工事故多米诺效应定量评价研究［J］.中国安全生产科学技术，2008，4（2）：49-52.

LIU Li，XU Ya-bo，LIU Zhen-yi.Progress on quantitative risk assessment of domino effect in chemical accidents［J］.Journal of Safety Science and Technology，2008，4（2）：49-52.

［2］师立晨，刘骥，魏利军，等.重大危险源多米诺效应的后果分析［J］.中国安全生产科学技术，2007，3（6）：44-48.

SHI Li-chen，LIU Ji，WEI Li-jun，et al.Consequence analysis for domino effect of major hazardous installations［J］.Journal of Safety Science and Technology，2007，3（6）：44-48.

［3］Cozzani V，Gubinelli G，Antonioni G，et al.The assessement of risk caused by domino effect in quantitative area risk analysis［J］.Journal of Hazardous materials，2005，127（1）：14-30.

［4］Cozzani V，Gubinelli G，Salzano E.Escalation thresholds in the assessment of domino accidental events［J］.Journal of Hazardous Materials，2006，129（1）：1-21.

［5］Khan F I，Abbasi S A.DOMIFFECT（DOMIno eFFECT）：User-friendly software for domino effect analysis［J］.Environmental Modellling ＆ Software，1998，13（2）：163-177.

［6］Hauptmanns U.A Monte-Carlo based procedure for treating the flight of missiles from tank explosions［J］.Probabilistic Engineering Mechanics，2001，16（4）：307-312.

［7］Hauptmanns U.A procedure for analyzing the flight of missiles from explosions of cylindrical vessels［J］.Journal of Loss Prevention in the Process Industries，2001，14（5）：395-402.

［8］Gubinelli G，Zanelli S，Cozzani V.A simplified model for the assessment of the impact probability of fragments［J］.Journal of Hazardous Materials，2004，116（3）：175-187.

［9］杨玉胜，吴宗之.储罐爆炸碎片最可能抛射距离的Monte-Carlo（蒙特卡罗）数值模拟［J］.中国安全科学学报，2008，18（3）：15-21.

YANG Yu-sheng，WU Zong-zhi.Monte-Carlo numerical simulation on the most probable flight distance of fragments from explosion of storage tanks［J］.China Safety Science Journal，2008，18（3）：15-21.

［10］邢志祥，蒋军成，赵晓芳.液化石油气储罐爆炸碎片抛射的蒙特卡罗分析［J］.火灾科学，2004，13（1）：39-42.

XING Zhi-xiang，JIANG Jun-cheng，ZHAO Xiao-fang.Monte-Carlo analysis of the flight of missiles from LPG tank explosion［J］.Fire Safety Science，2004，13（1）：39-42.

［11］张新梅，陈国华.爆炸碎片抛射速度及飞行轨迹分析方法［J］.华南理工大学学报（自然科学版），2009，37（4）：106-200.

ZHANG Xin-mei，CHEN Guo-hua.Analysis methods of projection velocity and flight trajectory of explosion fragments［J］.Journal of South China University of Technology（Natural Science Edition），2009，37（4）：106-200.

［12］Lees F P.Loss prevention in the process industries［M］.2nd ed.Oxford：Butterworth／Heinemann，1996：73-102.

［13］Center for Chemical Process Safety（CCPS）.Guidelines for evaluating the characteristics of vapor cloud explosions，flash fires，and BLEVEs［M］.New York：American Institute of Chemical Engineers，1994：311-335.

［14］Holden P L，Reeves A B.Fragment hazards from failures of pressurized liquefied gas vessels［C］∥Institution of Chemical Engineers Symposium Series，Assessment and Control of Major Hazards.Manchester，England，1985，93（42）：205-220.

［15］Mébarki A，Mercier F，Nguyen Q B，et al.Structural fragments and explosions in industrial facilities.Part I：Probabilistic description of the source terms［J］.Journal of Loss Prevention in the Process Industries，2009，22：408-416.

［16］Mébarki A，Nguyen Q B，Mercier F.Structural fragments and explosions in industrial facilities.Part II：Projectile trajectory and probability of impact［J］.Journal of Loss Prevention in the Process Industries，2009，22：417-425.

［17］Pula R，Khan F I，Veitch B，et al.A model for estimating the probability of missile impact：Missiles originating from bursting horizontal cylindrical vessels［J］.Process Safety Progress，2007，26（2）：129-139.

Monte-Carlo analysis of the projectile fragments from cylindrical tank boiling liquid expanding vapor explosion accident＊

LIU Zhen-yi，HUANG Ping，XU Ya-bo
（State Key Laboratory of Explosion Science and Technology，Beijing Institute of Technology，Beijing100081，China）

The generation and flight of fragments are stochastic and can cause more severe hazards.Studying on the domino effect study caused by the fragments from explosion is hotspot and difficulty.Based on dynamic analysis，the present work extended the two-dimensional fragment trajectory equation into three-dimensional system，and took wind into account.The present analysis took a cylindrical tank in Mexico City with boiling liquid expanding vapor explosion as an example，and the trajectory of fragment was simulated by Monte-Carlo method.Seen from the probabilities of fragment ranges to be reached with／without wind，wind has less impact on the hazard caused by fragments.The impact probability of a fragment on a target with no wind was attained，impact probability with the tank showed the increase of distance between the strict exponential decay trend，and through this relationship，the tank spacing in compliance with safety requirements can be calculated.The paper provides a method which is of great significance for the risk assessment and control of fragments from the explosion of cylindrical tanks.

mechanics of explosion；boiling liquid expanding vapor explosion；Monte-Carlo method；fragment；cylindrical tank

16July 2009；Revised 14September 2009

LIU Zhen-yi，zhenyiliu＠bit.edu.cn

（责任编辑 曾月蓉）

O389；X937 国标学科代码：130·35

A

2009-07-16；

2009-09-14

国家科技重大专项基金项目（2008ZX05054）

刘振翼（1975— ），男，博士后，讲师。

1001-1455（2010）06-0569-08

Supported by the National S＆T Major Project（2008ZX05054）