电子纵向初速度在氢原子蜘蛛状动量谱干涉结构中的作用*
2022-09-30何宇飞张贵忠付国跃盛泉史伟姚建铨
何宇飞 张贵忠 付国跃 盛泉 史伟 姚建铨
(天津大学精密仪器与光电子工程学院,光电信息技术教育部重点实验室,天津 300072)
使用半经典回碰模型和求解含时薛定谔方程的方法,数值研究了电离电子的纵向初速度在氢原子的蜘蛛状动量谱干涉结构中的作用.对光电子动量谱的纵向和横向动量分布性质的数值研究结果表明,可以从光电子动量谱的纵向动量分布获取电离电子纵向初速度的信息.研究发现,无论将初速度视为多个常数亦或是多段分布,均能重建完整的蜘蛛状干涉结构,可见用常数值来描述电子的初速度有待深入研究.另外,数值求解含时薛定谔方程的结果也与半经典回碰模型的模拟结论相一致,可以互相印证.本文的研究结果表明,纵向初速度在强激光脉冲电离产生的光电子动量谱中起着重要作用,速度的分布情况还需结合非绝热过程深入研究.
1 引言
在原子分子与光物理领域,理解原子分子的隧穿电离过程是理解许多强场现象的关键[1].电离后,电子在激光场作用下可能引发如高次谐波产生[2,3]、非顺序双电离[4]和激光诱导电子衍射[5]等丰富的强场现象.因此,人们对隧穿电离的隧穿概率、隧道出口位置、隧穿时间、电离电子的初始速度等隧穿电离过程的特性进行了研究[6-10].在绝热领域中,人们忽略隧穿电离过程中的激光电场变化,常将电子的初始纵向初速度取为零(这里的“纵向”指与激光偏振方向相平行的方向).但是当激光场频率较高时,由于激光场变化快于隧穿电离过程,需要考虑电离过程的非绝热效应.2012 年,Pfeiffer等[11]用考虑了隧穿电子的非零纵向初速度分布的半经典模型,很好地解释了氦原子电离的实验数据.此后,人们在不少实验与理论模型中对非零的纵向初速度进行了研究[12-25].目前科学界对于纵向初速度的分布情况还没有达成共识[17-21],不过研究已发现隧穿电子的纵向初速度对于原子种类和激光参数等条件敏感[22].事实上,在目前对纵向初速度分布的研究中,大多考虑了这个问题两方面中的一个: 1) 将初速度假设为一个中点位于零、有一定宽度的分布;2) 或将初速度假设为一个非零的常数值.例如,在理论方面,量子轨迹蒙特卡罗法考虑了初始速度分布[8];在实验方面,采用正交双色场测量的初速度是基于单一速度值的假定[25],结果较为精确.本研究考虑了这两种情况,但研究发现在半经典回碰模型(semiclassical rescattering model,SRM)框架下,从所诱导的干涉结构难以区分这两情况.
在电离后,光电子在交变激光场作用下运动,人们将直接远离原子核而不折返的电子称为参考电子,将在激光场作用下返回原子核并与之发生碰撞的电子称为信号电子.研究发现由参考电子与信号电子之间的干涉会在光电子动量谱(photoelectron momentum distributions,PMDs)中形成蜘蛛状的干涉结构[26],其中蕴含了丰富的原子结构信息与电离电子的动力学信息.唐久等[27]结合半经典回碰模型和含时薛定谔方程(time-dependent Schrödinger equation,TDSE)方法,基于干涉较小位置对散射振幅相位的依赖关系,提出了一种提取蜘蛛状光电子动量谱的散射振幅相位的近似方法.
在本文中,考虑非绝热效应,采用了包含隧穿电子非零纵向初速度的SRM 模型对氢原子隧穿电离产生的PMDs 进行数值模拟,SRM 理论是一种基于三步模型的半经典理论[28-33].成功得到了发生回碰的信号电子与直接电离的参考电子间发生干涉产生的蜘蛛状干涉结构.在模型中取不同的纵向初速度,通过对PMDs 的切割得到纵向和横向动量分布,分析了纵向初速度在蜘蛛状干涉结构中的作用.作为对比,数值求解TDSE 同样模拟了蜘蛛状动量谱干涉结构,以进一步印证SRM 模型计算结果中的发现与结论.
2 数值方法
SRM 理论模型不仅计算方便,而且能提供直观的物理图像.本文使用该模型来模拟参考电子与信号电子间的干涉现象,对蜘蛛状干涉结构进行数值研究.
在模拟中,假设激光脉冲为线偏振,且偏振方向沿x轴:
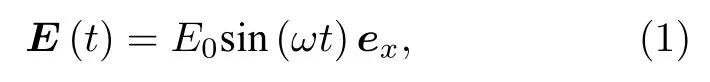
其中E0是激光脉冲强度,ω是脉冲载波频率.电离后,电子的初始位置在原子核处,在激光场作用下运动.信号电子沿x轴方向的速度可表示为
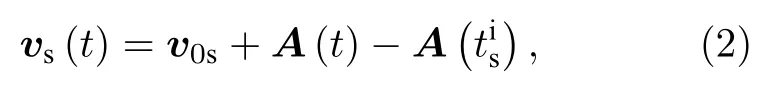
其中vs(t)是信号电子的速度,v0s是信号电子的初速度,A(t)是激光场的矢势,是信号电子的电离时刻.对(2)式两侧积分,可得信号电子的位置,由此能计算信号电子的运动轨迹:
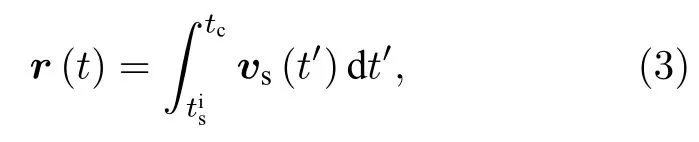
其中tc是回碰时刻.因为若发生回碰,电子在回碰时刻将回到原子核,即回到原点处,可通过如下关系计算回碰时刻tc:

在回碰后,电子的散射角度θ在—90°到+90°之间,信号电子的最终动量可以表示为
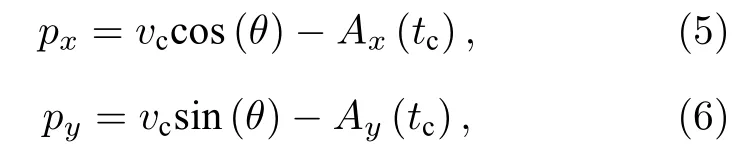
其中px和py就是PMDs 中的最终动量,vc是信号电子在回碰时刻tc的瞬时速度,Ax和Ay是激光场矢势在x,y方向上的分量.
参考电子与信号电子间若要发生干涉,它们的最终动量需相等.对于参考电子,依据正则表达式,其电离时刻、初速度v0r和最终动量pf有如下关系:

参考电子的速度可表示为
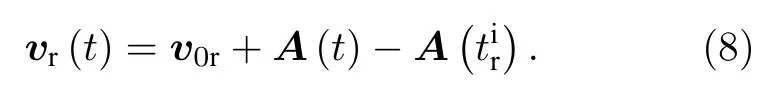
参考电子和信号电子之间的相位差可表示为
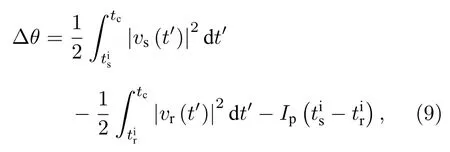
其中Ip是原子的电离势.
最后,PMDs 上的干涉结构(其中,I代表干涉强度)是由(9)式中的相位差所决定的:
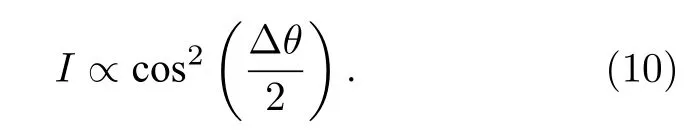
作为对比,本文通过数值求解TDSE 也得到了包含蜘蛛状干涉结构的PMDs.在计算中,采用了波函数分离技术[33].在长度规范下,含时薛定谔方程为
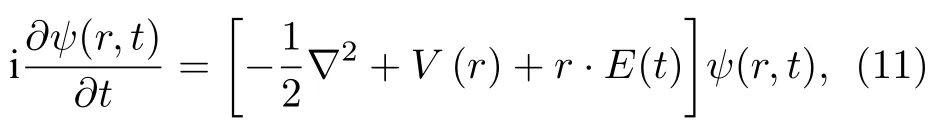
其中V(r)=是库仑势,b是软化参数,E(t)是激光电场.
本文中选取的激光参数为: 激光载波频率为0.8 eV,脉冲持续时间为2 个光学周期,激光强度为4×1013W/cm2.除特别说明外,均采用上述的激光参数条件.本文也在一定范围内对这些参数进行了改变,以保证数值模拟的结果的可靠性和可重复性.
3 结果与讨论
本文使用SRM 模型对PMDs 中的蜘蛛状干涉结构进行了大量数值模拟.首先,考虑电离电子的初速度为不含分布的常数值的情况.图1(a)—(c)是取信号电子的纵向初速度分别为0,0.2 和0.4 a.u.时,采用上述SRM 理论模型模拟得到的PMDs.由于单一常数值的纵向初速度的选取,PMDs 中的蜘蛛状干涉结构并不完整,但每张图中都能明确地观察到沿纵向分布的干涉结构.
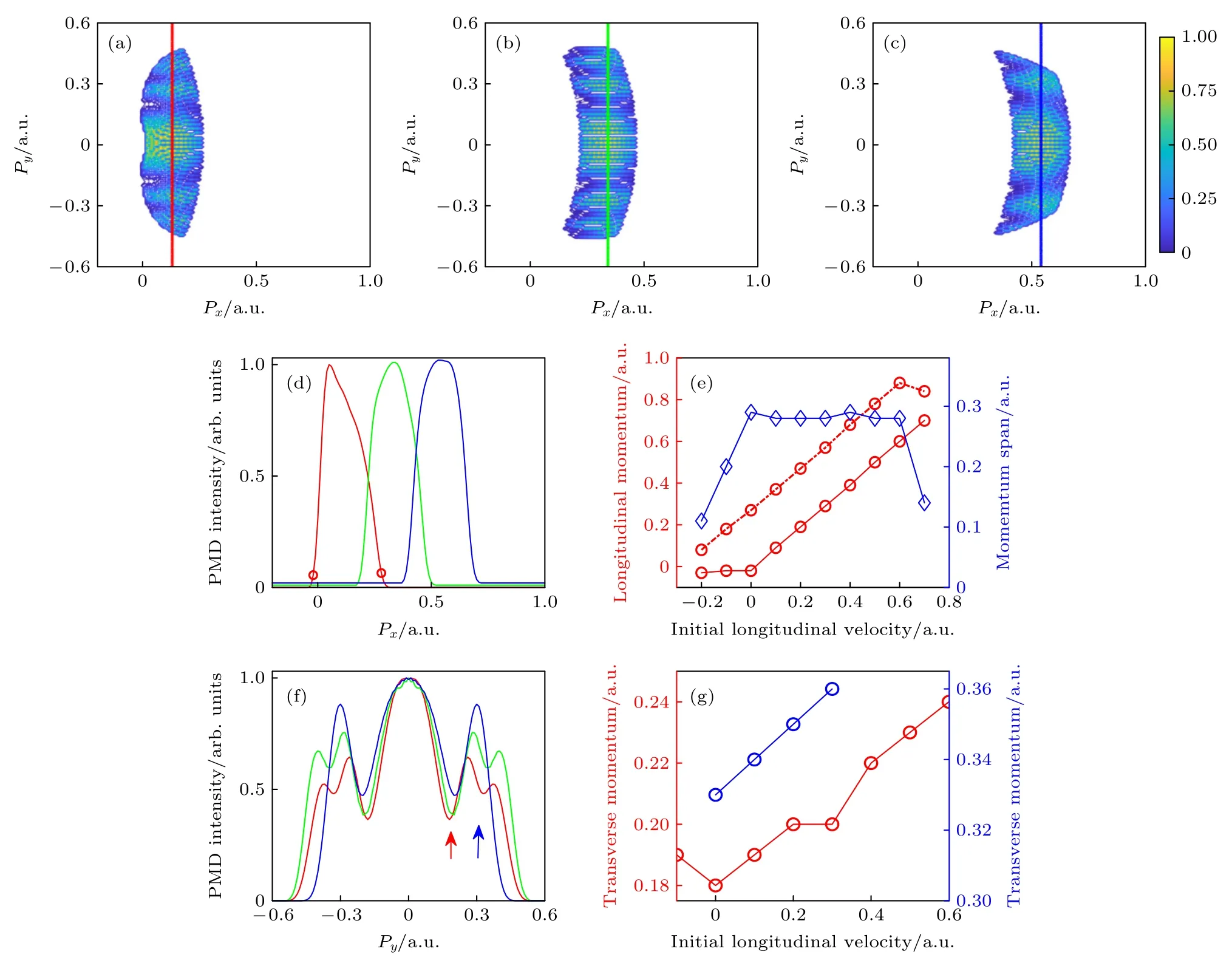
图1 (a)—(c) 使用SRM 模型得到的氢原子PMDs.电子初速度取为常数,分别是(a) 0 a.u.,(b) 0.2 a.u.和 (c) 0.4 a.u.,其中彩色竖线标注了之后对动量谱作横向切割的动量位置,归一化的色度条衡量动量谱的强度,后文中的色度条同理.(d) 图1(a)—(c)中动量谱的纵向动量分布;(e) 纵向动量分布的左边界(红实线)、右边界(红虚线)和动量分布的宽度(蓝)随纵向初速度变化的曲线图.(f) 图1(a)—(c)中动量谱的横向动量分布;(g) 横向动量分布的第一(红)和第二(蓝)干涉极小位置随纵向初速度变化的曲线图.图1(d)和图1(f)中红色、绿色和蓝色曲线分别与图1(a)—(c)相对应,后文的横向和纵向动量分布曲线亦如是标记Fig.1.(a)—(c) Spiderlike PMDs of hydrogen atom simulated by SRM for nonzero offset and zero distribution.The initial velocity is(a) 0 a.u.,(b) 0.2 a.u.,and (c) 0.4 a.u.,respectively.The vertical lines in the figures interpret the longitudinal momentum positions for the transverse cut-plot curves (see below),and the normalized colorbar represents the intensity of the PMD.(d) Longitudinal cut-plot curves taken at py=0 a.u.;(e) the left boundary momentum (red solid line),the right boundary momentum (red dash-dotted line) and the width or span of the longitudinal momentum distributions (blue).(f) Transverse cut-plot curves.The red and blue arrows mark the first and second interference minima;(g) the transverse momentum positions of the first and second interference minima as a function of the initial velocity.The red,green and blue curves in the figures correspond to Fig.1 (a),Fig.1 (b) and Fig.1 (c),and the same is true of the following PMDs.
为对干涉结构进行分析,对PMDs 沿纵向和横向方向进行了切割.顺着x轴方向作纵向切割的动量位置均取py=0 a.u.处,顺着y轴方向作横向切割的动量位置由PMDs 中竖直实线所标注.图1(d)和图1(f)是对图1(a)—(c)中PMDs 作切割得到的纵向和横向动量分布.由图1(d)可见,一个纵向初速度为常数的电子对一定最终动量范围内的PMDs都存在贡献.为对动量分布定量描述,定义纵向动量分布的左边界和右边界为其峰值大小的1/10 处的动量位置,如图1(d)中的红色圆圈所示;定义纵向动量分布的宽度为其左边界和右边界之差.图1(e)是对应不同初速度的纵向动量分布的左边界、右边界和动量分布宽度.可见,随着初速度的增加,PMDs的分布会在纵向上朝着高动量区域移动.当初速度在0—0.6 a.u.之间时,纵向动量分布的宽度保持在0.28 a.u.附近不变.然而,当初速度低于0 a.u.或高于0.6 a.u.时,动量分布的宽度会迅速减小,这意味着此时对应该初速度的电子将难以发生回碰.至此可见,PMDs 的分布与电子的纵向初速度是紧密相关的.
取纵向动量分布左右边界的中点处,对PMDs作横向切割,得到如图1(f)所示的横向动量分布.本文主要关注横向分布的第一和第二干涉极小值的动量位置,横向分布上的每一个极小值都对应着PMDs 中蜘蛛状干涉结构的一条蜘蛛腿,如图1(f)中箭头所示.图1(g)是横向动量分布的第一和第二干涉极小值的动量位置随纵向初速度的变化规律,其中第二干涉极小值仅在初速度处在适当大小范围内才可被识别.第三和更高的干涉极小将更为模糊,难以识别,在此不做考虑.可以发现,随纵向初速度增大,第一和第二干涉极小位置也会缓慢地增大.数值研究发现该规律对于动量更高阶的极值也成立.
除了常数值的纵向初速度,还取电子的纵向初速度为一个中点偏移了零的分布.图2(a)—(c)是取电子的纵向初速度分别为0—0.2 a.u.,0.2—0.4 a.u.和0.4—0.6 a.u.的分布时得到的PMDs.这些PMDs与图1 中的结果十分相似,这是因为将初速度取为一个分布的情况,可以被简单理解为无数个从初速度为常数值情况相加.图2(d)和图2(e)是该PMDs的纵向和横向动量分布.可见,PMDs 的纵向动量分布的宽度基本不变,而其横向动量分布的宽度则变化较大,两者存在着不同.

图2 (a)—(c)使用SRM 模型得到的PMDs.电子初速度取为分布,分别是(a) 0—0.2 a.u.,(b) 0.2—0.4 a.u.,(c) 0.4—0.6 a.u.;(d) 图2(a)—(c)中动量谱的纵向动量分布;(e) 图2(a)—(c)中动量谱的横向动量分布Fig.2.(a)—(c) Spiderlike PMDs simulated by SRM for nonzero offset and nonzero distribution.The initial velocity ranges are (a) 0 to 0.2 a.u.,(b) 0.2 to 0.4 a.u.,and (c) 0.4 to 0.6 a.u.,respectively.(d) Longitudinal cut-plot curves;(e) transverse cut-plot curves.
接下来,将假设的纵向初速度分布的范围扩大至—0.5—1.0 a.u.,得到如图3(a)的PMDs,这一范围保证了全部可能的回碰电子初速度都被考虑在内.该动量谱中存在着完整且典型的蜘蛛状干涉结构,在上下两侧分别有两条清晰的蜘蛛腿结构.动量谱呈现出一个心形结构,这是因为在模拟中仅考虑了电子—40°—40°的回碰散射角度,更大散射角度的电子对图中动量谱的贡献可被忽略.同时可见,随着纵向初速度的增大,第二干涉极小变得逐渐模糊,如前所述,第三或更高的干涉极小不予考虑.
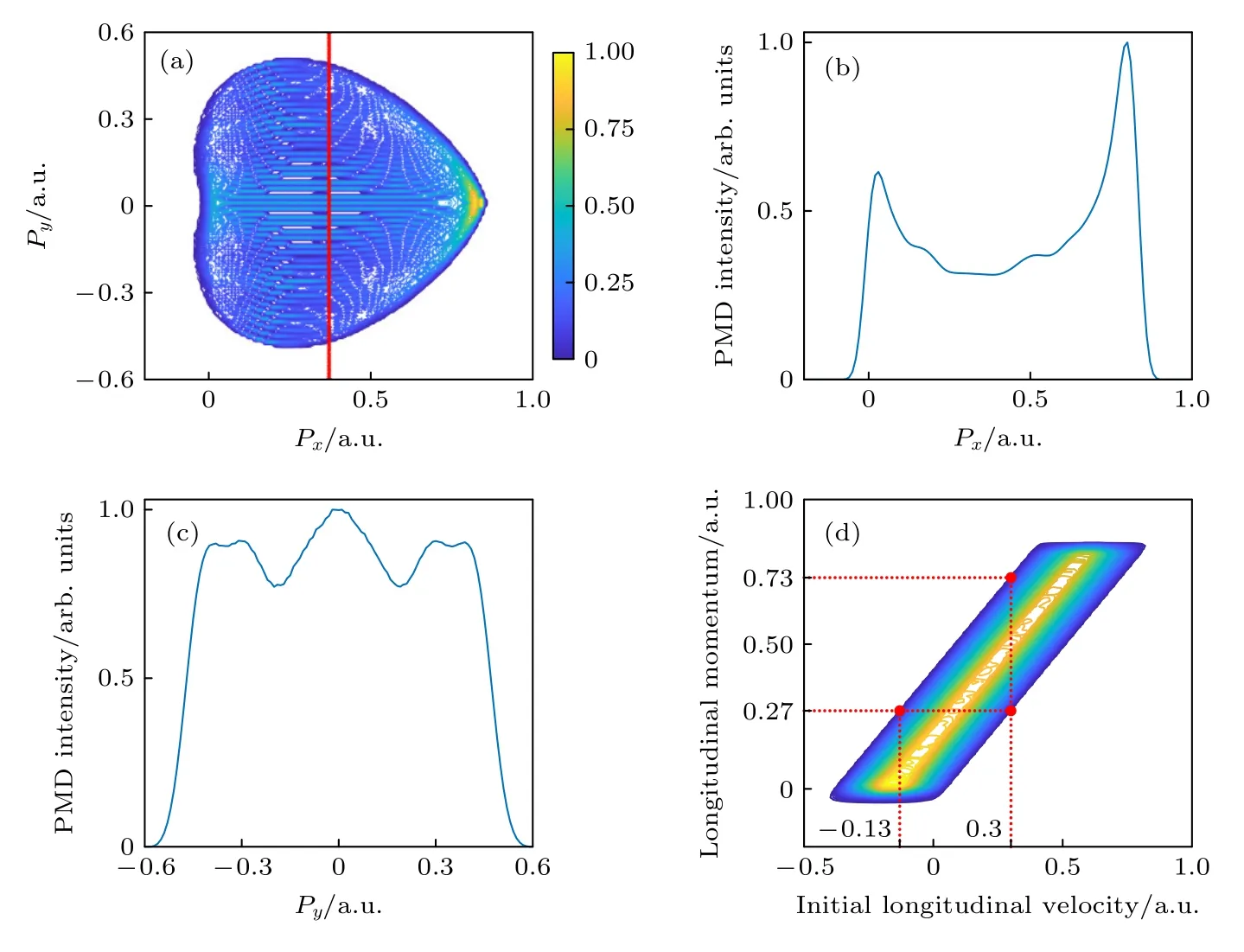
图3 使用SRM 模型得到的PMDs (a) 电子初速度为—0.5—1 a.u.的光电子动量谱;(b) 图3(a)中动量谱的纵向动量分布;(c) 图3(a)中动量谱的横向动量分布;(d) 图3(a)中动量谱的纵向初速度与最终纵向动量之间的变化关系Fig.3.Spiderlike PMDs simulated by SRM: (a) PMDs with wider initial velocity range of —0.5 to 1.0 a.u.;(b) longitudinal cut-plot curve;(c) transverse cut-plot curve;(d) the relationship between the final longitudinal momentum and the initial longitudinal velocity.
图3(d)是数值模拟过程中记录下来的纵向初速度与最终纵向动量之间的对应关系,可以观察到一个明显的线性关系,即初速度越大,最终动量越大,这与图1(e)中两条红色曲线的趋势相对应,也与Li 等[25]工作中发现的规律相同.根据这一关系,可以推断一个纵向初速度为常数值的信号电子的最终动量的取值范围;反过来,也可推断一个最终动量为常数值的信号电子的纵向初速度的取值范围.以图3(d)为例,若确定电子纵向初速度为0.30 a.u.,在图中横坐标0.3 a.u.处作垂线,通过垂线在图中交点的纵坐标大小,可以确定最终纵向动量的取值范围在0.27—0.73 a.u.;反之,若确定最终纵向动量为0.27 a.u.,在纵坐标0.27 a.u.处作垂线,同理可通过交点位置判断纵向初速度的取值范围在—0.13—0.30 a.u.间.该方法无法精确地将电子纵向初速度与最终纵向动量一一精确对应,而只能确定大概范围.这是因为如前文分析,同一初速度的电子对PMDs 上一定最终动量范围内的强度都存在贡献,而不同初速度的电子在同一最终动量处的PMDs 上均可存在贡献.它们是相互叠加,而非一一对应的关系.此外,通过图3(d)中曲线的左下角和右上角动量位置,可确定纵向初速度的最小值和最大值分别为—0.40 a.u.和0.82 a.u.,最终纵向动量的最小值和最大值分别为—0.05 a.u.和0.85 a.u.由此可见,电子纵向初速度的大小在PMDs 中起着重要作用.在理论上,基于单一速度值假设,采用强场近似理论拟合实验数据,获得了较为精确的纵向初速度值[25].
本文还研究了激光脉冲强度对纵向初速度和PMDs 的影响.图4(a)—(c)所对应的激光脉冲强度分别为2×1013,4×1013和8×1013W/cm2.图4(d)和图4(e)分别为其纵向和横向动量分布,图4(f)是纵向动量分布的左右边界和宽度随初速度变化的曲线图.纵向看,由图4(f)可知,随着激光强度增大,动量分布的左边界几乎保持不变,而右边界和动量分布的宽度会线性增大;横向看,动量分布的极值位置没有明显的位移,但随激光强度增大,在高动量区域有更高阶的蜘蛛腿出现.图4(g)—(i)是对应不同激光强度下的纵向初速度与最终纵向动量之间的对应关系,可见更高的激光强度能够允许包含更高初速度和最终动量的干涉结构的存在.
为了研究PMDs 中的焦散,Kelvich 等[16]建立了一个考虑了库仑作用对电子初速度影响的半经典理论.基于该理论,对应图4(g)—(i)的激光参数条件,经计算可得,考虑由库仑作用引起的漂移动量修正后的电子纵向初速度分别为0.075,0.106和0.150 a.u.,这与本文数值模拟所取的纵向初速度处于同一量级.

图4 变化激光脉冲强度时,使用SRM 模型得到的PMDs (a)—(c) 激光强度增大时,对应的PMDs;(d) 图4(a)—(c)中动量谱的纵向动量分布;(e) 图4(a)—(c)中动量谱的横向动量分布;(f) 纵向动量分布的左边界(红实线)、右边界(红虚线)和动量分布的宽度(蓝)随纵向初速度变化的曲线图;(g)—(i) 图4(a)—(c)中动量谱的纵向初速度与最终纵向动量之间的变化关系.对应的激光脉冲强度分别为 (a),(g) 2×1013 W/cm2;(b),(h) 4×1013 W/cm2;(c),(i) 8×1013 W/cm2Fig.4.Spiderlike PMDs simulated by SRM: (a)-(c) Spiderlike PMDs simulated by SRM with increasing laser intensities;(d) longitudinal cut-plot curves;(e) transverse cut-plot curves;(f) the left boundary momentum (red solid line),right boundary momentum(red dash-dotted line) and the width of the longitudinal momentum distributions (blue);(g)-(i) the relationship between the final longitudinal momentum and the initial longitudinal velocity.The laser intensity is: (a),(g) 2×1013 W/cm2;(b),(h) 4×1013 W/cm2;(c),(i) 8×1013 W/cm2.
为了研究常数值的初速度和分布的初速度之间的区别,分别取电子的初速度为多个常数或为多段分布.图5(a)是一个包含完整蜘蛛状干涉结构的光电子PMDs,其纵向初速度取为—0.5—1.0 a.u.;图5(b)是取初速度为五个单独的常数值得到的PMDs;图5(c)是取初速度为五段分离的分布得到的PMDs;图5(d)是图5(a)—(c)中PMDs 的纵向动量分布,其中绿色和蓝色曲线中的多个峰值是由于相邻两个或两段初速度对PMDs 强度的贡献相叠加而引起的.可见,无论是由多个单值还是多段分布的初速度均能成功重建出完整的PMDs,且它们有着相同宽度的纵向动量分布.这说明,从PMDs中提取电子的常数值初速度的研究是并不准确的,因为由一个为分布而非常数值的电子初速度也能得出相同的PMDs.
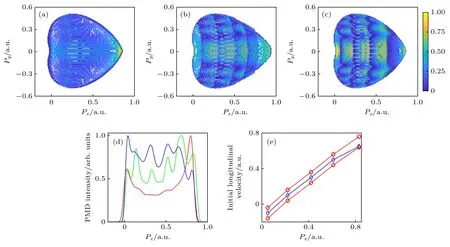
图5 使用有多个常数或多段分布的初速度的SRM 模型重建完整的PMDs (a) 取电子初速度为—0.5—1 a.u.,使用SRM 模型得到的完整PMDs;(b) 取电子初速度为多个不同的常数值,使用SRM 模型得到的PMDs;(c) 取电子初速度为多段不同的分布,使用SRM 模型得到的PMDs;(d) 图5(a)—(c)中动量谱的纵向动量分布;(e) 模拟中取的电子初速度,蓝色曲线对应图5(b),红色曲线对应图5(c)Fig.5.(a) Spiderlike PMDs simulated by SRM with initial velocity range of —0.5 to 1.0 a.u;(b) spiderlike PMD reconstructed by adding five PMDs each generated with a nonzero offset (no offset distribution);(c) spiderlike PMD reconstructed by adding five PMDs each generated with a nonzero offset distribution;(d) longitudinal cut-plot curves with the red,green and blue colors corresponding to Fig.5(a)—(c);(e) the initial velocities of the five PMDs.The blue curve represents the initial velocities in Fig.5(b),and the red curves represent the initial velocity ranges in Fig.5(c).
为验证变化激光强度时SRM 模型的模拟结果,通过数值求解TDSE 的方法,同样得到了具有蜘蛛状干涉结构的PMDs.图6(a)对应的激光脉冲强度为 8×1013W/cm2.图6(b)和图6(c)分别是该PMD 的纵向和横向动量分布,其中用红色曲线表示纵向动量分布的包络.这里类似SRM 模型情况,同样定义了纵向动量分布的左边界、右边界和动量分布的宽度,并将它们随激光强度的变化规律画于图6(d)中.基于Kelvich 等[16]的理论,计算了对应这些激光强度下电子的纵向初速度,并将其标注于图6(d)的上坐标轴中.可以发现,随激光强度增大,纵向动量分布的左边界维持在约0.7 a.u.处不变,而右边界和动量分布的宽度线性增大,该变化趋势也与由SRM 模型得到的图4(f)一致.
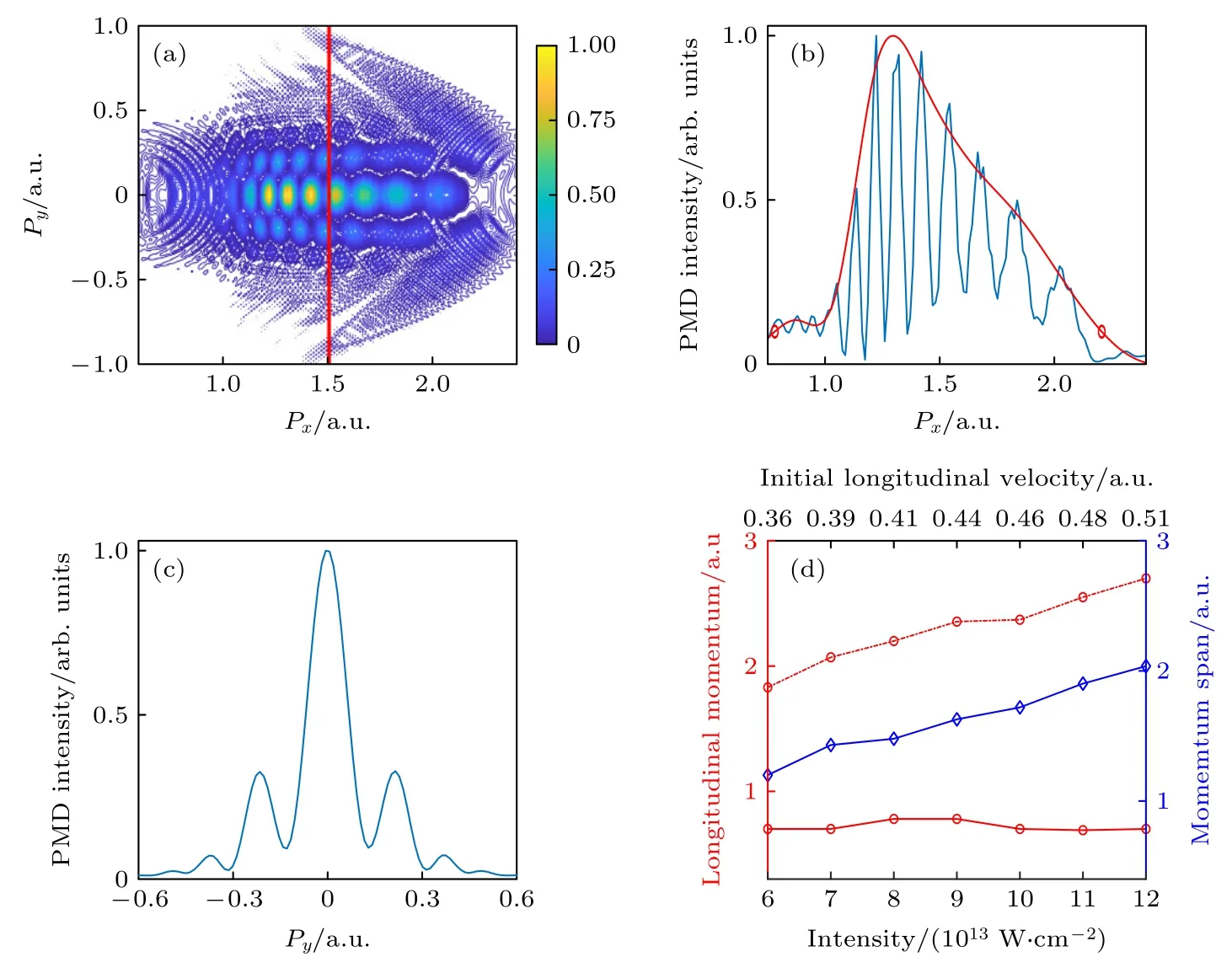
图6 (a) 取激光脉冲强度为8×1013 W/cm2 时,数值求解TDSE 得到的PMD;(b) 图6(a)中动量谱的纵向动量分布;(c) 图6(a)中动量谱的横向动量分布;(d) 纵向动量分布的左边界(红实线)、右边界(红虚线)和动量分布的宽度(蓝)随纵向初速度变化的曲线图Fig.6.(a) Spiderlike PMD simulated by TDSE with laser pulse intensity of 8×1013 W/cm2;(b) longitudinal cut-plot curve;(c) transverse cut-plot curve;(d) the left boundary momentum (red solid line),right boundary momentum (red dash-dotted line)and the width or span of the longitudinal momentum distributions (blue) with respect to different laser intensities or initial velocities.
4 结论
本文使用SRM 模型和求解TDSE 的方法进行了大量数值模拟,成功得到了具有蜘蛛状动量谱干涉结构的PMDs.在SRM 模型中考虑了非绝热效应,给电离电子设定非零的纵向初速度,该初速度可以是一个常数也可是一个分布.通过对PMDs的纵向和横向动量分布的分析,研究了纵向初速度在PMDs 中的作用.数值结果表明,可以从PMDs中反求出电子纵向初速度的取值范围.此外,发现无论取纵向初速度为多个不同的常数还是多段分布,均能重建出包含完整蜘蛛状干涉结构的PMDs,可见将初速度视为一个常数的研究并不够准确,还需更深入的研究.最后,通过数值求解TDSE 同样得到了蜘蛛状干涉结构,将其与SRM 模型的计算结果作了对比与印证.
