流动系统中爆轰波传播特性的数值模拟*

潘振华，范宝春，归明月，张旭东

（南京理工大学瞬态物理国家重点实验室，江苏 南京 210094）

流动系统中爆轰波传播特性的数值模拟*

潘振华，范宝春，归明月，张旭东

（南京理工大学瞬态物理国家重点实验室，江苏 南京 210094）

基于带化学反应的二维Euler方程，采用氢气／空气的9组分19步基元反应简化模型，对充有当量比的氢气／空气预混气体的矩形爆轰流场中爆轰波的传播过程进行了数值模拟，讨论了均匀来流对爆轰波传播的影响。数值结果表明，在均匀来流的影响下，上游方向上的燃烧强度大于C-J爆速，下游方向上的燃烧强度小于C-J爆速；上游方向传播的爆轰波的阵面压力大于下游方向传播的爆轰波的阵面压力。所以，经典的C-J爆轰理论并不适用于流动系统中爆轰波传播特性的研究。

爆炸力学；爆轰波；C-J爆轰理论；流动系统

1 引 言

与传统推进相比，爆轰推进系统具有热效率高、结构简单等特点，近年来受到较为广泛的关注。根据其工作原理，可将爆轰发动机分为3类：脉冲爆轰发动机（PDE）［1］、驻定爆轰发动机（ODWE）［2］和旋转爆轰发动机（RDE）［3］。脉冲爆轰发动机通过在燃烧室中周期性地充气、点火、爆轰生成、传播和泄出产生脉冲推力；驻定爆轰发动机则设法将爆轰波驻定在燃烧室内，从而使超音速流动的未燃气体在爆轰阵面内快速稳定燃烧，进而产生推力；而旋转爆轰发动机则使爆轰波在燃烧室进气端绕着中心轴旋转，而爆轰产物由出气端泄出，从而产生推力。显然，无论何种爆轰发动机，其中的爆轰波都是在流动系统中传播的，例如：对于脉冲爆轰，爆轰波的传播方向与波前气体的流动方向一致（顺风传播）；对于驻定爆轰，爆轰波的传播方向与波前气体的流动方向相反（迎风传播）；而对于旋转爆轰，爆轰波的传播方向则主要与波前气流方向垂直（横向传播）。现行的经典爆轰学主要讨论静止介质中的爆轰波，而对于流动介质中的爆轰波，经典的爆轰理论是否适用成为研究爆轰发动机时必须关注的问题。

W.W.Mackenna［4］对等当量比的氢气／氧气混合物中，气流马赫数在0.14～4.0之间变化时，爆轰波向上游传播的特性进行了实验研究。结果表明，气流速度较低时，对爆轰传播速度影响较小，其值与静止系统中爆轰的C-J值基本一致；但当气流速度远高于音速时，爆轰波相对于来流的传播速度将高于C-J值。L.E.Curtis等［5］对上述结论作了进一步的实验验证。A.A.Vasil’ev等［6］在加热风洞中研究流动系统中的爆轰传播，结果表明，爆轰波向上游传播时，爆速高于C-J值，向下游传播时，则低于C－J值。K.Ishii等［7］和H.Kataoka等［8］对激波诱导的流动系统中的爆轰传播进行了实验研究，测试了爆轰的传播速度、流场的压力和爆轰的胞格结构，结果表明：向上游传播的爆轰波，爆速高于C-J值，胞格被压缩；向下游传播的爆轰波，爆速降低，胞格被拉长。T.H.Li等［9］通过数值模拟讨论了一维流动系统中的爆轰波，得出与上述实验一致的结论。

本文中以氢气／空气预混气为研究对象，基于带化学反应的二维Euler方程，对爆轰波在流动系统中的传播过程（包括上游传播、下游传播和横向传播）进行数值研究，并根据计算结果，对流动系统中爆轰波的传播特性进行讨论。

2 数学模型

2.1 控制方程

忽略质量扩散，热传导和粘性，在二维平面坐标系中，考虑基元化学反应的流动守恒方程（Euler方程组）为

式中：cV（T）＝∑cVk（T）Yk为混合物的比定容热容，Yk为组分k的质量分数，h0k为组分k的生成焓，T为温度。

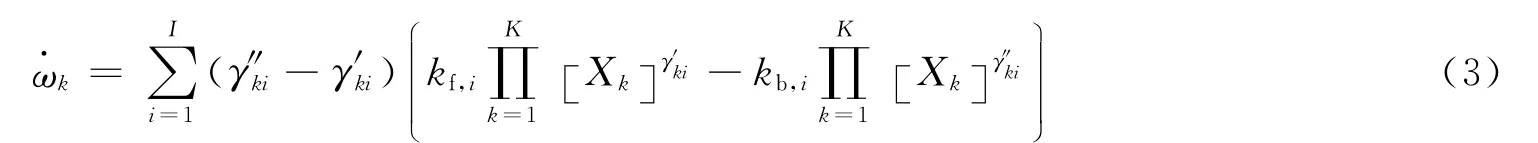
式中：Af，i为i个正反应的指前因子；βf，i为第i个正反应的温度指数；Ef，i为第i个正反应的活化能。

2.2 计算方法

不同过程特征时间的差异引起方程的刚性问题，为此，采用分裂格式，将控制方程中的对流项和化学反应项分开处理。对流过程采用带有MC（monotonized centered）限制器的、考虑横传波影响的波传播算法［10］；对于化学反应过程的刚性问题则采用基于Gear算法的隐式方法。

本文中采用的计算格式已经在文献［11］中得到验证。

2.3 算例

图1为计算域简图。长0.26m，宽0.1m的燃烧室，左侧为进气端，右侧为出口端。等当量比的氢气／空气预混气以1km／s的流速在燃烧室内从左向右流动，设其初始状态为p0＝101.325kPa，T0＝298.15K。长0.08m、宽0.02m的爆轰管与燃烧室相连，为防止燃烧室中流动气体对爆轰管流场的影响，两者间用薄膜隔离，爆轰管另一端为起爆端（图中黑色区域）。爆轰管内充满组分和初始状态与燃烧室内的气体相同的静止气体，起爆端的初始条件为T＝10T0，p＝10p0。

计算采用结构化网格，燃烧室所用网格数为325×125，爆轰管所用网格数为25×100。燃烧室的左边和右边均为出口敞开边界，下底边和爆轰管相通，其余壁面均为固壁，爆轰管上底边和燃烧室相通，其余3个面均为固壁。

对于氢气／空气混合物的反应，采用含19个基元反应和9组分的化学反应机理［11］。

图1 计算区域示意图Fig.1The computational domain

3 计算结果与讨论

当水平管内为静止气体时，垂直管内的爆轰波传入水平管，爆轰波在外突角绕射，由于拐角处膨胀波的影响，爆轰波在水平方向先熄灭，然后再生，如图2所示［12］，流场是关于垂直管对称的。

计算结果如图3所示。其中图3（a）为某瞬时流场绕射爆轰波的流场图，＊表示爆轰波出现再生的位置。图3（b）为不同时刻流场的压力等势分布图，它描述了流场的变化过程，反映了流场变化过程中的对称性。

爆轰波由垂直管进入水平管后，在两侧出现突角绕射，拐角处出现膨胀波，因此流线发散，零水平速度分量的虚线构成的三角区内，为未受膨胀波扰动的区域；垂直虚线右侧的质点向右运动，左侧的质点向左运动。在绕射初始阶段，下壁面附近的爆轰波熄火，在离垂直管轴线24.3mm处，重新再次成长为C-J爆轰。向两侧传播的爆轰波强度相同，爆轰波后的压力突跃值相同，传播速度相同。

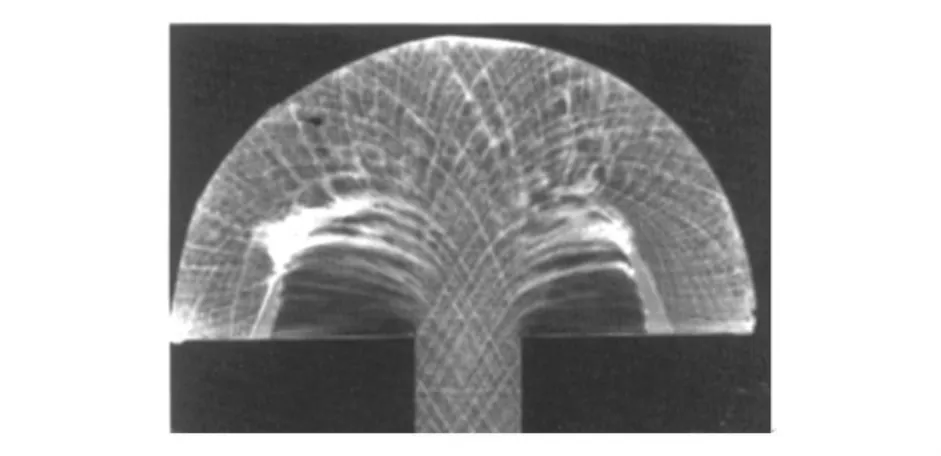
图2 T型管中爆轰波绕射的实验照片Fig.2 Measured picture of the diffracted detonation in T-shape bifurcated tube

图3 T型管中静止系统的爆轰波绕射计算流场Fig.3 Calculated Flow field of the diffracted detonation with quiescent system in T-shape bifurcated tube

水平管内为流动气体时，爆轰波的绕射流场将因此发生变化。图4为水平管中气体以1km／s的速度从左向右运动时，绕射爆轰波的计算流场图。其中图4（a）为某瞬间流场，图4（b）为不同时刻流场的压力等势分布图。

显然，对于右突角，爆轰波绕射时，波后流场在膨胀波影响下，流线是发散的；但对于左突角，无论流动气体还是爆轰波后气体，流线都向着压缩方向折转，故拐角处不存在因膨胀而导致的压力下降。从下壁面压力分布曲线可以看出，左拐角的压力远高于右拐角的压力。因此，正如图中＊点所示，右传爆轰的再生距离（离轴线48.0mm处）远大于左传爆轰的再生距离（离轴线20.3mm处）。由于水平管中的气体定向流动，图4（a）中，零水平速度分量虚线向左侧大幅移动。该线右侧质点向右运动，左侧质点向左移动，但右传波后，质点向右运动的速度远大于左传波的质点向左运动的速度。由此可见，爆轰波在从左向右的运动系统中绕射后，向上游传播的带化学反应的激波，其波后的压力分布要高于向下游传播的波；其波后传播方向上的质点运动速度的分布远小于向下游传播的波。

爆轰波绕射后，经过一段时间的发展，在流动气体的顺流、逆流和横向3个方向上皆可形成稳定传播的爆轰波，计算结果表明，逆流传播的爆轰波稳定爆速为1.923km／s，顺流传播的爆轰波稳定爆速为2.032km／s，横向传播的爆轰波稳定爆速为1.952km／s，根据 Gordon-McBrid［13］程序计算的 C-J爆速为1.963km／s。

图5（a）为爆轰波上3个阵面元a、b和c稳定传播时的压力剖面图。为了便于比较，图5（b）为对应于图5（a）中3个压力剖面的对比图。由图可见，上游方向传播的爆轰波（即阵面元a），其阵面压力达到1.66MPa；横向方向传播的爆轰波（即阵面元b），其阵面压力为1.37MPa；下游方向传播的爆轰波（即阵面元c），其阵面压力为1.18MPa。由此可以得出：上游、横向、下游方向压力强度依次递减。这与文献［9］关于流动系统中爆轰传播的一维数值计算结果结论一致。

图4 T型管中流动系统的爆轰波绕射计算流场Fig.4 Calculated Flow field of the diffracted detonation with incoming system in T-shape bifurcated tube

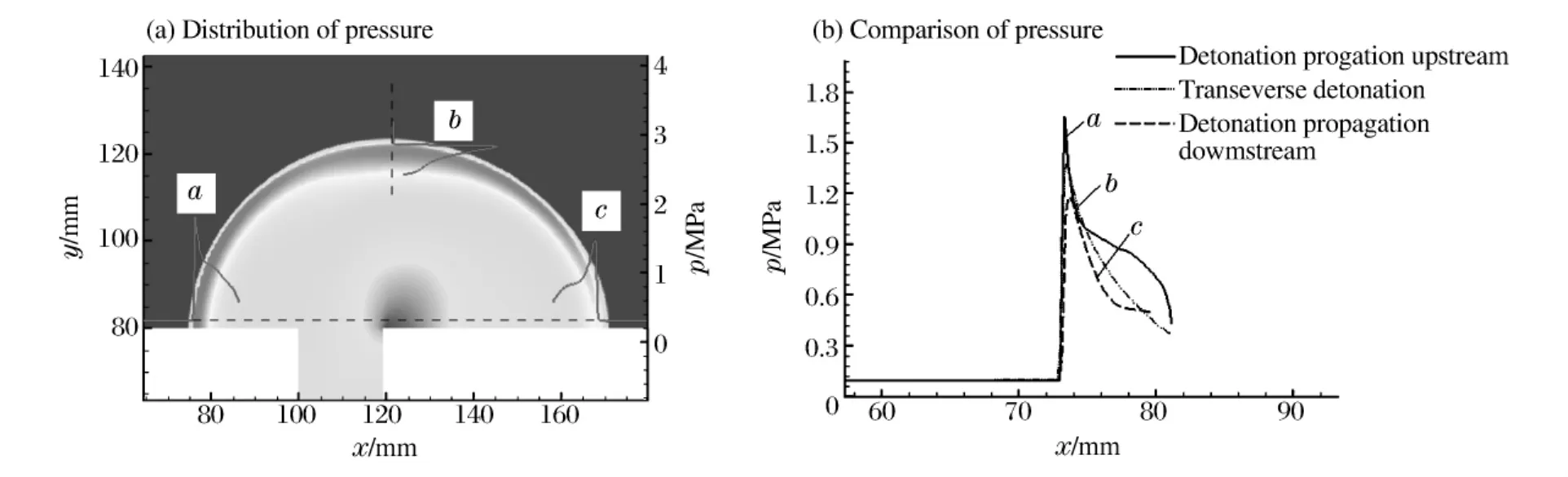
图5 爆轰波不同阵面上的压力强度Fig.5 The strength of pressure of detonation fronts in different directions

从以上分析结果来看，上游方向的压力较下游方向的压力大，与静止流场中爆轰波的传播相比，上游、下游波阵面压力强度不成轴对称相等。

4 结 论

（1）在均匀来流中传播的爆轰波由于受到垂直方向气流的影响，爆轰波波形有向下游偏移的趋势。

（2）爆轰波在从左向右的运动系统中绕射后，向上游传播的带化学反应的激波，其波后的压力分布要高于向下游传播的波；其波后传播方向上的质点运动速度的分布远小于向下游传播的波。

（3）爆轰波由于受到均匀来流的影响，上游、横向、下游方向上的压力强度依次递减。

（4）经典的C-J爆轰理论并不适用于本文中描述的流动系统中爆轰波传播的研究。

［1］Roy G D，Frolov S M，Borisov A A，et al.Pulse detonation propulsion：Challenges，current statues and future perspective［J］.Progress in Energy and Combustion Science，2004，30（6）：545-672.

［2］Ramakanth M，Vijaya S.Preliminary design of a pulse detonation based combined engine［R］.ISABE 2001-1212，2001.

［3］Daniau E，Falempin F，Bykovskii F A，et al.Continuous detonation wave propulsion systems：First step toward operational engines［R］.ISABE 2005-1302，2005.

［4］Machkenna W W.Interaction between detonation waves and flowfields［J］.AIAA Journal，1967，5（5）：868-873.

［5］Curtis L E，Hamilton L A，Wright H E，et al.An investigation of shock initiated detonation waves in a flowing combustible misture of hydrogen and oxygen［J］.Acta Astronautica，1970，15：453-463.

［6］Vasil’ev A A，Nalivaicenko D G，Zvegintsev V I.Detonation waves in supersonic of homogeneous reacting mixture［R］.ICDERS20 2005-19，2005.

［7］Ishii K，Kataoka H，Kojima T.Initiation and propagation of detonation waves in combustible high speed flows［J］.Proceedings of the Combustion Institute，2009，32（2）：2323-2330.

［8］Kataoka H，Kojima T，Ishii K.Propagation of detonation in a combustible supersonic flow［R］.ICDERS21 186，2007.

［9］Yi T H，Wilson D R，Lu F K.Numerical study of unsteady detonation wave propagation in a supersonic combustion chamber［R］.ISSW25 10041，2004.

［10］Leveque R J.Wave propagation algorithms for multidimensional hyperbolic systems［J］.Journal of Computational Physics，1997，131（2）：327-353.

［11］归明月，范宝春，于陆军，等.聚心火焰与激波相互作用的数值研究［J］.爆炸与冲击，2007，27（3）：204-209.

GUI Ming－yue，FAN Bao-chun，YU Lu-jun，et al.Numerical investigations on interaction of implosion flame with shock［J］.Explosion and Shock Waves，2007，27（3）：204-209.

［12］Lee J H S.Dynamics of Exothermicity［M］.New York：Gordon and Breach Science Publishers，1995：321-335.

［13］Gordon S，Mcbride B J.Computer program for calculation of complex chemical equilibrium compositions and application：Analysis［R］.NASA RP-1311，1994.

Numerical simulation of detonation wave propagation in a flow system＊

PAN Zhen-hua，FAN Bao-chun，GUI Ming－yue，ZHANG Xu-dong
（Laboratory of Transient Physics，Nanjing University of Science and Technology，Nanjing210094，Jiangsu，China）

The rectangular detonation flow field filled with hydrogen-air is simulated numerically based on multicomponent two-dimensional Euler equation，and effects of uniform incoming flow on detonation wave propagation were discussed.From the numerical results，depending on the flow velocity，the apparent propagation velocity of a detonation wave is higher in the upstream direction and lower in the down stream direction than vC－J.The pressure of the upstream moving detonation is higher than that of the downstream moving detonation.As a result，investigation of detonation wave propagation in a flow system by classical C-J detonation theory is unsuitable.

mechanics of explosion；detonation wave；C-J detonation theory；flow system

13July 2009；Revised 23November 2009

FAN Bao-chun，bcfan＠mail.njust.edu.cn

（责任编辑 曾月蓉）

O382 国标学科代码：130·35

A

1001-1455（2010）06-0593-05

2009-07-13；

2009-11-23

国家自然科学基金项目（10872096）

潘振华（1981— ），男，博士。

Supported by the National Natural Science Foundation of China（10872096）