两栖作战武器非线性横摇动力学研究

马新谋,潘玉田,常列珍,范昱珩

(1.中北大学,山西太原 030051;2.中国兵器科学研究院,北京 100089)

两栖作战武器非线性横摇动力学研究

马新谋1,潘玉田1,常列珍1,范昱珩2

(1.中北大学,山西太原 030051;2.中国兵器科学研究院,北京 100089)

为了研究两栖作战武器非线性横摇动力学,在借鉴船舶非线性横摇动力学理论的基础上,利用两栖武器水上性能分析计算软件计算某两栖武器的GZ曲线,在考虑了流体附加质量转动惯性矩和非线性阻尼项的前提条件下,建立了两栖作战武器非线性横摇动力学方程,即将该方程化为无量纲形式,并引入状态变量,将二阶非自治动力学方程化为一阶自治动力学方程组,采用四阶龙格库塔法求解,给出了两栖武器在不同频率的波浪扰动下的非线性横摇角位移和角速度响应,并给出了不同工况下的系统相图。结果表明,两栖作战武器在规则波浪的扰动下的横摇运动是一个非线性动力学问题,其动力学特性对参数敏感。

基础力学;两栖作战武器;横摇运动;阻尼力矩

从事船舶横摇运动研究工作的学者发现船舶横摇运动与其稳性有着密切的关系[1-6],因此两栖作战武器水上的横摇运动直接影响其水上性能、乘员的战斗力和射击精度。徐国英、马新谋等人[7-8]在关于两栖作战武器水上的横摇运动问题的研究中仅涉及到线性横摇运动问题。借鉴船舶研究的经验,两栖作战武器水上横摇运动是一个强非线性动力学问题,用线性理论描述两栖作战武器水上的横摇运动不能揭示其运动本质,有必要对两栖作战武器在波浪作用下的非线性横摇动力学进行分析研究。

1 非线性横摇运动动力学方程

仿照船舶非线性横摇动力学方程建立两栖作战武器非线性横摇运动方程[9-10],设横摇角为 φ,则两栖作战武器非线性横摇运动微分方程为:

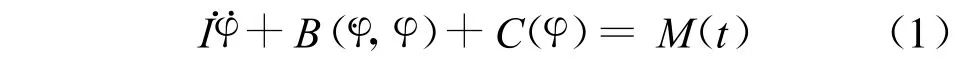
惯性项可以写为[3,9-10]:

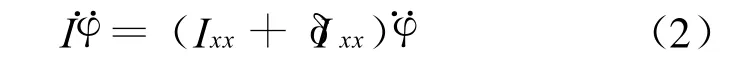
式中:Ixx为两栖作战武器横摇质量转动惯性矩;δ Ixx为流体附加质量转动惯性矩。

在研究船舶的非线性横摇时,众多的学者给出了不同的阻尼项和回复项形式,本研究参考Taylan[10]的研究给出两栖作战武器横摇的阻尼项和回复项形式为:

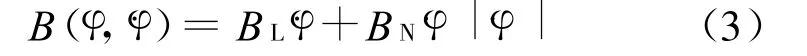
式中:BL为线性阻尼项系数;BN为非线性阻尼项系数。

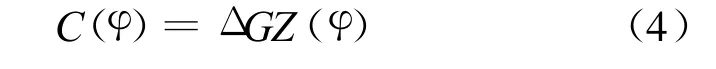
式中:Δ为两栖作战武器的排水量;GZ(φ)为回复力臂,回复力臂可以用φ的奇数型三多项式次表示为:

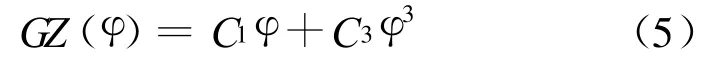
为简单起见,先研究两栖作战武器在规则波浪的激励下的非线性横摇运动,规则波浪的扰动力矩为[11]:

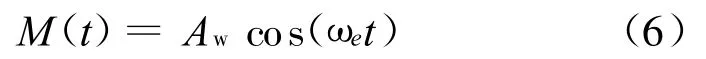
式中:Aw为波浪扰动力矩幅值;ωe为遭遇波浪的频率。

把式(2)～式(6)代入式(1)可得两栖作战武器非线性横摇运动微分方程为:

把式(7)转换成无量纲形式:

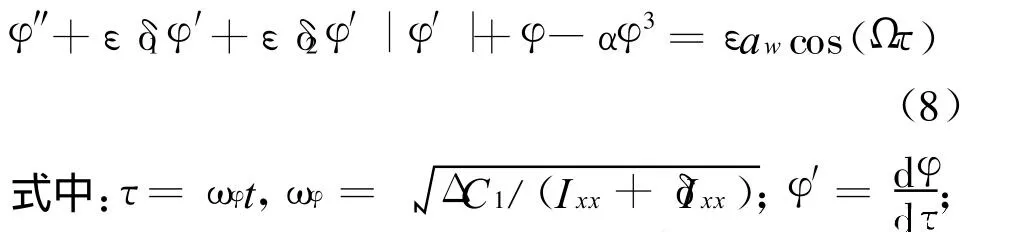
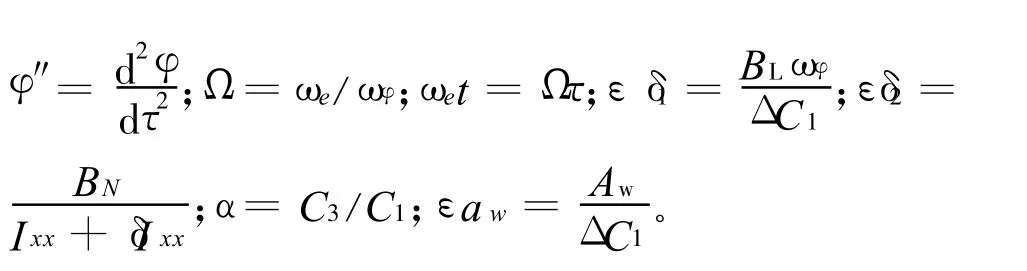
某两栖作战武器的排水量为196 kN;横摇质量转动惯性矩为95 kg·m2;BL=52 kg·m2·s-1;BN=18 kg·m2;Aw=500 N·m。根据船舶的分析计算经验,取流体附加质量转动惯性矩δ Ixx为全武器系统横摇质量转动惯性矩Ixx的20%。采用作者开发的两栖作战武器水上性能分析计算软件计算得到该武器的回复力臂曲线如图1所示。

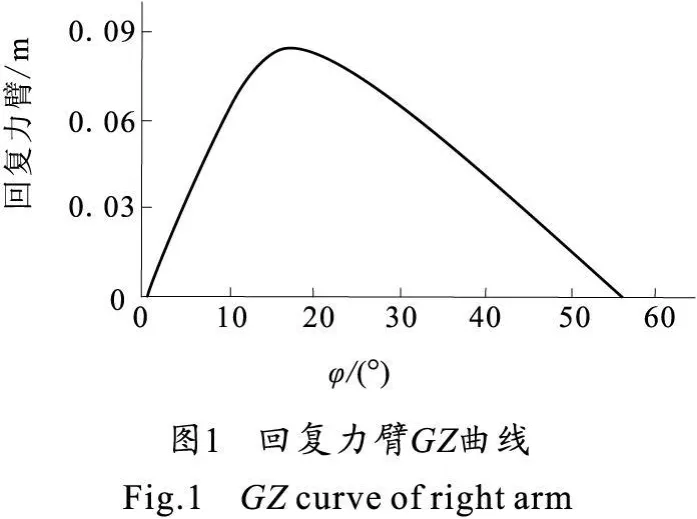
根据回复力臂GZ曲线,用最小二乘法拟合出GZ(φ)=C1φ+C3φ3的系数为 :C1=0.2035;C3=-0.231 8,则有α=1.1391;ωφ =18.704 6;ε δ1=0.024 4;ε δ2=0.157 9;ε aw=0.012 5 。

2 非线性横摇运动分析

为了分析方便,引入状态变量x(τ)表示横摇角位移,y(τ)表示横摇角速度,z(τ)表示 Ω τ,则两栖作战武器非线性横摇运动状态由状态变量 x(τ)和y(τ)所体现。非自治方程(8)可改写为由不显含时间的状态变量一阶自治微分方程组:

设状态变量的初始条件为:当τ=0时,x(0)=x0,y(0)=y0

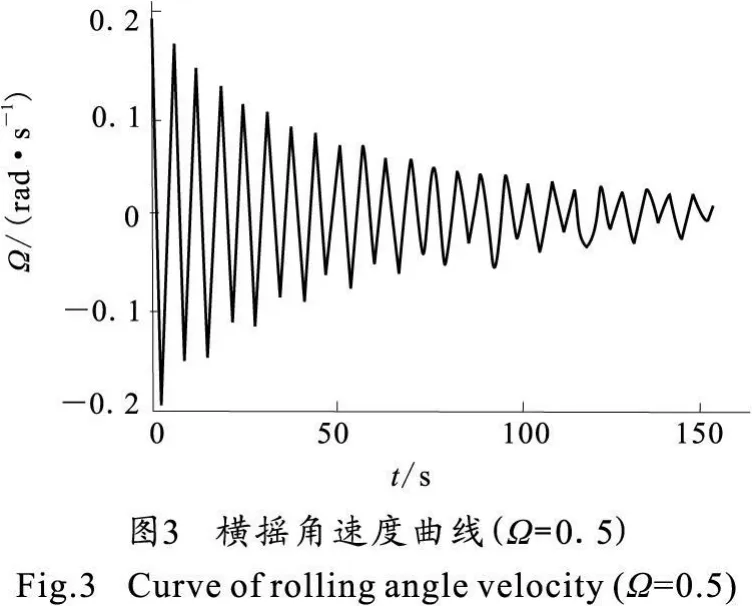
采用四阶龙格库塔法求解微分方程组(9)可以得出两栖作战武器非线性横摇运动运动状态。根据给定的状态变量的初始条件:当t=0时,x(0)=0,y(0)=1.1,z(0)=0。当波浪角频率与该两栖作战武器的固有角频率之比Ω为0.5时,计算结果如图2～图4所示。

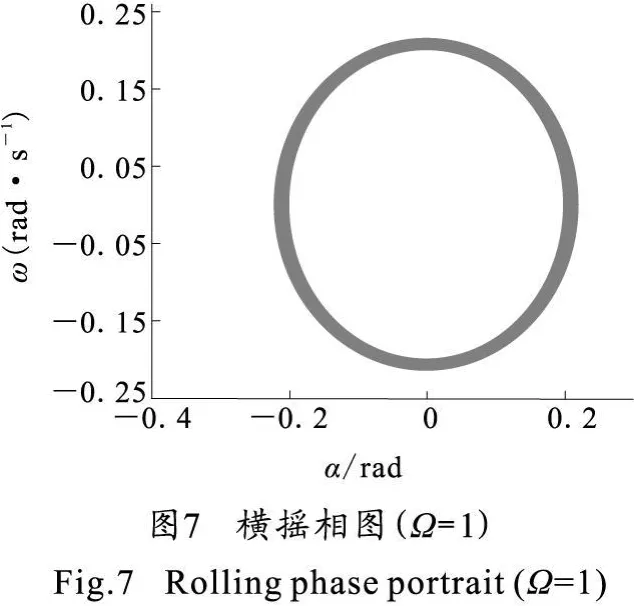
当Ω=1时,波浪角频率与该两栖作战武器的固有角频率相等,即发生了共振,系统的运动状态计算结果如图5～图7所示。

当Ω=2时,即波浪角频率与该两栖作战武器的固有角频率的2倍,系统的运动状态计算结果如图8～图10所示。

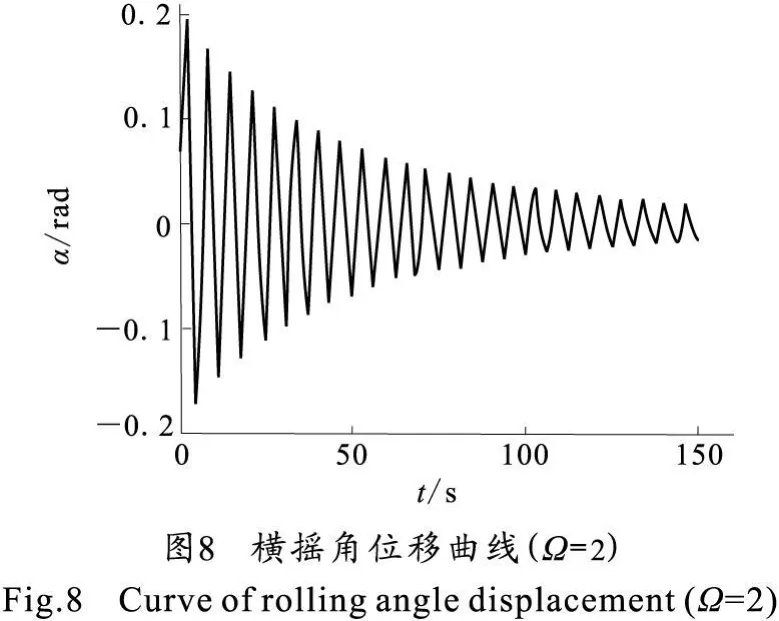
由图2、图5和图8可知,两栖武器横摇角位移与波浪的频率和与两栖武器横摇固有频率之比 Ω直接相关。当Ω=1时,两栖武器横摇角位移很大,如图5所示出现了横摇共振现象;当 Ω=0.5和Ω=2时,两栖武器横摇角位移很快衰减,如图2和图8所示横摇角位移曲线已不是线性系统的规则正弦或余弦(衰减)曲线了,表现出了明显的非线性特性。

由图3、图6和图9可知,两栖武器横摇角速度与Ω也直接相关。当Ω=1时,两栖武器横摇角速度很大,如图6所示出现了共振现象;当 Ω=0.5和Ω=2时,两栖武器横摇角位移很快衰减,如图3和图9所示。

由图4、图7和图10可知,两栖武器横摇相图与Ω关系密切。当 Ω=1时,两栖武器横摇相图很规矩,是一个近圆环形,如图7所示;当 Ω=0.5和Ω=2时,两栖武器横摇相图出现了混乱。

3 Lyapunov特性指数计算

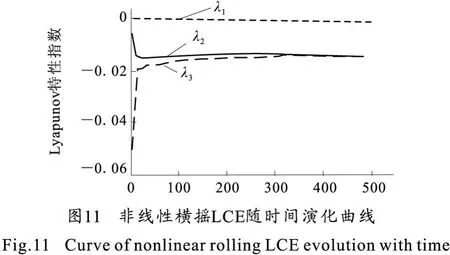
那么两栖武器的非线性横摇运动是否进入混沌状态呢?非线性动力学系统是否进入混沌状态可由其吸引子的类型来判断。众所周知,Lyapunov特性指数(LCE)[12]可以对耗散系统的吸引子进行分类,而两栖武器的非线性横摇运动是典型的耗散系统。因此,需要计算在规则波浪的扰动下两栖型自行火炮水上非线性横摇的LCEλi(i=1,2,3),非线性横摇LCE随时间演化曲线如图11所示。

由图11可以看出,该两栖型自行火炮水上非线性横摇最大LCEλ1随着时间的演化趋于0,LCEλ2随着时间的演化趋于-0.01 285,LCEλ3随着时间的演化趋于-0.013 33。由计算的LCE的符号可知,该两栖型自行火炮水上非线性横摇运动的吸引子类型为极限环,可以判断其运动为周期性的运动。

4 结 论

通过以上分析可以得出如下结论:

1)两栖作战武器横摇运动是一个强非线性的周期运动,其动力学特性对参数敏感。

2)回复项的非线性可以用切片理论完美地得到解决,提高拟合GZ曲线的次数可以有效提高其贴近实际的程度。

3)阻尼项和惯性项的非线性参数的获取是其横摇动力学分析的关键,直接影响分析的精度。

References)

[1]张文斌,姚震球,蒋志勇.船舶稳性理论研究的方法及进展[J].华东船舶工业学院学报:自然科学版,2002,16(1):7-11.

ZHANG Wen-bin,YAO Zhen-qiu,JIANG Zhi-yong.Study and advance of the theory of stability of ship[J].Journal of East China Shipbuilding Institute:Natural Sciences Edition,2002,16(1):7-11.(in Chinese)

[2]张寿桂.船舶在大风浪中横摇稳性变化的理论研究[J].中国舰船研究,2006,1(1):50-53.

ZHANG Shou-gui.Theoretical study method for roll stability of ships in waves[J].Chinese Journal of Ship Research,2006,1(1):50-53.(in Chinese)

[3]袁远,余音,金咸定.船舶在规则横浪中的奇异倾覆[J].上海交通大学学报,2003,37(7):995-998.

YUAN Yuan,YU Yin,JIN Xian-ding.Undesirable ship capsizal in regular beam sea[J].Journal of Shanghai Jiaotong University,2003,37(7):995-998.(in Chinese)

[4]董艳秋,纪凯,黄衍顺.波浪中船舶横摇稳性的研究[J].船舶力学,1999,3(2):1-6.

DONG Yan-qiu,JI Kai,HUANG Yan-sun.Study on the ship stability in rolling in waves[J].Journal of Ship Mechanics,1999,3(2):1-6.(in Chinese)

[5]唐友刚,林维学,董艳秋,等.船舶参数激励和强迫激励作用下的非线性运动响应[J].中国造船,2001,42(2):34-39.

TANG You-gang,LIN Wei-xue,DONG Yan-qiu,et al.Nonlinear motion response of ship under parametric excitation and forced excitation[J].Ship Building of China,2001,42(2):34-39.(in Chinese)

[6]李远林,王冬姣.船舶大幅横摇运动[J].船舶力学,2004,8(1):26-34.

LI Yuan-lin,WANG Dong-jiao.Large-amplitude rolling motion of a ship[J].Journal of Ship M echanics,2004,8(1):26-34.(in Chinese)

[7]徐国英,周景涛,姚新民,等.两栖车辆在波浪中的摇荡问题研究[J].兵工学报,2005,26(4):433-437.

XU Guo-ying,ZHOU Jing-tao,YAO Xin-min,et al.Toss motion of amphibious vehicle in sea-way[J].ACTA Armamentarii,2005,26(4):433-437.(in Chinese)

[8]马新谋,潘玉田,马昀.两栖作战武器线性横摇运动动力学分析[J].火炮发射与控制学报,2008(2):85-88.

M A Xin-mou,PAN Yu-tian,MA Yun.Linear roll motion dynamics analysis of amphibious combat weapon[J].Journal of Gun Launch&Control,2008(2):85-88.(in Chinese)

[9]吴秀恒.船舶操纵性与耐波性[M].北京:人民交通出版社,1998:200-230.

WU Xiu-heng.Manoeuvring and seakeeping characteristics of ship[M].Beijing:China Communications Press,1998:85-88.(in Chinese)

[10]TAYLAN M.The effect of nonlinear damping and restoring in ship rolling[J].Ocean Engineering,2000,27:921-932.

[11]SURENDRAN S.Non-linear roll dynamics of a Ro-Ro ship in waves[J].Ocean Engineering,2005,32:1818-1828.

[12]UDWADIA F E,BREMEN H F.An efficient and stable approach for computation of Lyapunov characteristic exponents of continuous dynamical systems[J].Applied M athematics and Computation,2001,121:219-259.

Study on Nonlinear Rolling Motion Dynamics of Amphibious Combat Weapon

MA Xin-mou1,PAN Yu-tian1,CHANG Lie-zhen1,FAN Yu-heng2

(1.North University of China,Taiyuan 030051,Shanxi,China;
2.China Ordnance Science Institute,Beijing 100089,China)

In order to study nonlinear rolling dynamics of the amphibious combat weapon,with the aid of nonlinear rolling dynamics theory of boats and ships,GZ curves of a amphibious combat weapon were calculated by means of the characteristics analysis and calculation software of amphibious combat weapon.The nonlinear rolling dynamics equation was established under the condition of taking the added mass inertia moment term,the nonlinear damping term and the nonlinear restoring moment term into account.The equation was simplified into non-dimensional form.Led into state variable,the second-order non-autonomous dynamics equation was rewritten as 3 first-order autonomous equations.Then the equations were solved by use of fourth-order Runge-Kutta method.Finally the rolling angle displacement-time history,rolling angle velocity-time history and phase portrait of amphibious combat weapon were given under different regular wave frequency.The results indicated that the rolling motion of amphibious combat weapon under regular wave is a problem of nonlinear dynamics system and its dynamics features are sensitive to parameters.

basic mechanics;amphibious combat weapon;rolling motion;damping moment

TJ81+0.1

A

1673-6524(2010)04-0066-04

2009-10-14;

2010-03-15

马新谋(1978-),男,博士研究生,主要从事自行火炮浮渡技术研究。E-mail:maxinmou03@163.com