再生式液体发射自动武器理论模型及参数影响规律研究

冉景禄,徐 诚,汪 冰

(南京理工大学机械工程学院,江苏南京 210094)

再生式液体发射自动武器理论模型及参数影响规律研究

冉景禄,徐 诚,汪 冰

(南京理工大学机械工程学院,江苏南京 210094)

针对液体发射技术应用于自动武器日益成为可能,提出了基于再生式液体发射的导气式自动武器概念模型,建立了能够全面真实反映其内弹道过程的零维数学模型,该模型包括储液室控制方程和内弹道方程和导气装置与自动机运动方程、耦合方程。利用参考文献研究成果验证了该模型的正确性。利用该模型探讨了结构参数对其内弹道特性的影响,得出了其影响的基本规律。该模型对研发基于再生式液体发射技术的导气式自动武器具有理论和实用价值。

机械学;液体发射;再生式液体发射药;自动武器;内弹道

由于具有烧蚀小、温度低和装填密度高等优点,使得国内外对液体发射技术的研究和探索已经持续了60多年[1]。目前,以文献[2-8]为代表的资料表明:尽管遇到各种困难,总体来讲,液体发射的相关研究正在逐步深入,相关关键技术不断取得突破。未来战争和非战争行动对自动武器提出了许多新的需求,如变初速发射、变(等)效能杀伤等,传统自动武器设计遇到挑战,而液体发射技术具有适应这些需求的特性。所以,据此可以预料,液体发射技术应用于自动武器只是时间问题。因此,十分有必要对相关问题进行预先研究。为此,本文提出了一种基于再生式液体发射技术的导气式自动武器的概念模型,建立了能够全面真实反映其内弹道过程的零维数学模型。较之文献[9-10]所建立的内弹道模型,本文的理论计算模型更为简单,更能够描述导气式武器内弹道中的变质量热力学过程。文末利用该模型,探讨了部分结构参数对内弹道特性的影响规律。

1 概念模型及基本假设

1.1 概念模型

基于再生式液体发射的导气式自动武器的概念模型如图1所示。在点火具的作用下,燃烧室会产生一个初始压力,当初始压力达到活塞启动压力后,再生喷射活塞在火药燃气的推动下向右运动,压缩贮液室内的液体,同时压缩喷射活塞复进簧,阀门关闭。当储液室压力上升至一定阈值后,液体火药开始由活塞喷孔高速喷入燃烧室燃烧,产生高温高压的火药燃气,当压力大于弹丸启动压力时,弹丸开始挤进膛线加速运动。弹丸运动到开孔位置时,火药燃气从导气孔流入导气室,进而推动导气活塞向后运动,此时,导气活塞上的凸台沿供弹具内圆的导槽运动,使得旋转供弹具发生旋转,随着导气活塞推自动机向后运动,在弹匣簧力的作用下,弹匣内的弹头向上运动到达待进位置,后坐终了后,自动机在导气复进簧的作用下向前运动,推到达待进位置的弹头上膛,与此同时,喷射活塞在喷射活塞复进簧的作用下向前运动,同时阀门打开,将液体发射药吸入储液室。

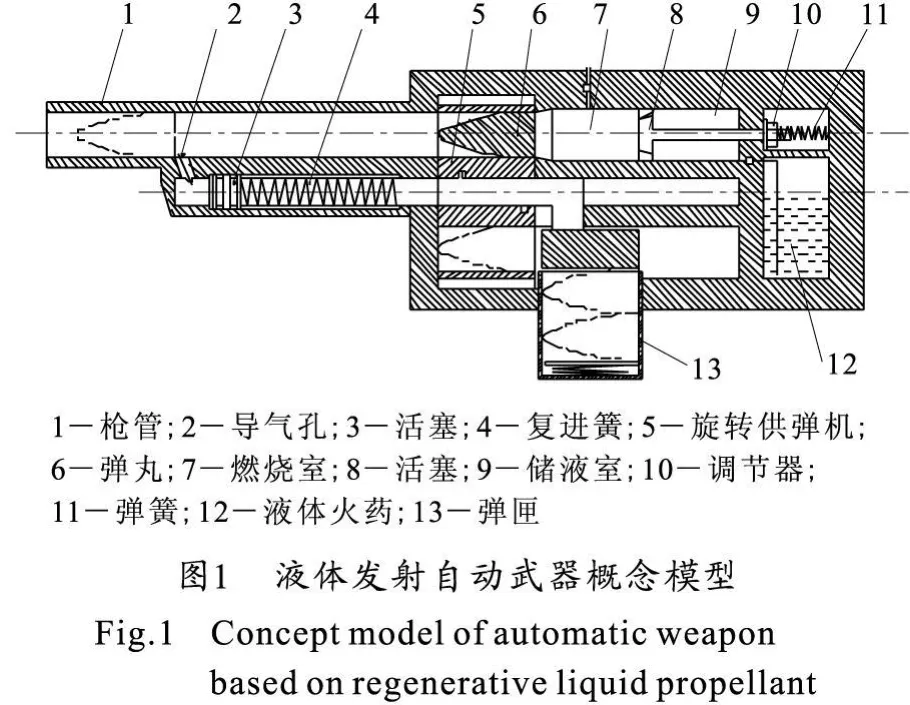
1.2 基本假设

1)结构是刚性的。

2)认为液体具有压缩性,忽略贮液室截面变化,认为贮液室流体为等熵流体。

3)忽略点火过程,假设从储液室喷入燃烧室的火药液滴瞬间完全燃烧。

4)导气装置内流场是一个有流入与流出的变质量热力学过程。

5)由于是瞬态计算,忽略火药燃气与枪管和导气室之间的热量交换。

6)内弹道与导气装置通过火药燃气流量相互耦合。

2 内弹道过程数学模型

内弹道过程数学模型包括:储液室控制方程、经典内弹道方程、导气装置与自动机运动方程、内弹道与导气装置耦合方程。

2.1 储液室控制方程

1)储液室液体密度方程

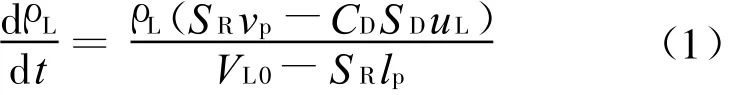
式中:ρL为储液室液体发射药密度;SR为贮液室断面积;lp为活塞运动位移;vp为活塞运动速度;CD为流量系数;SD为喷孔面积;VL0为贮液室初始容积;uL为液体药喷射速度。

2)储液室压力方程

式中:B为液体药体积模量;C为液体药体积模量系数。

3)活塞速度方程

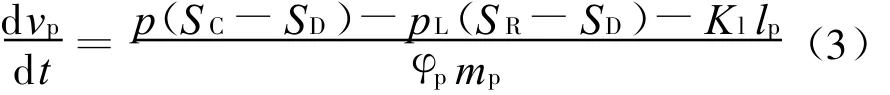
式中:Kl为药室复进簧刚度;φp为活塞运动次要功系数;SC为燃烧室断面积;mp为活塞质量。

4)液体药喷注控制方程采用非稳态的Bernoulli方程,同文献[1]中方程(8-96)。

5)液体药喷射相对质量流率同文献[1]中方程(8-96)。

6)活塞位移方程同文献[1]中方程(8-96)。

2.2 经典内弹道方程

1)内弹道基本方程

式中:f为火药力;l0为燃烧室初始长度;r为比热比;K1为药室复进簧刚度;Gb为导气孔处气体流量。

2)枪管内火药燃气密度方程

式中:ρ为膛内火药燃气密度;η为喷入燃烧室内火药的质量;η1为从枪管流入导气室的火药气体质量;V0为燃烧室初始容积。

3)弹丸速度方程同文献[1]中方程(8-96)。

4)弹丸位移方程同文献[1]中方程(8-96)。

5)燃烧室液体燃烧方程同上述的液体药喷射相对质量流率方程。

2.3 导气装置与自动机运动方程

1)气室内气体压力变化方程

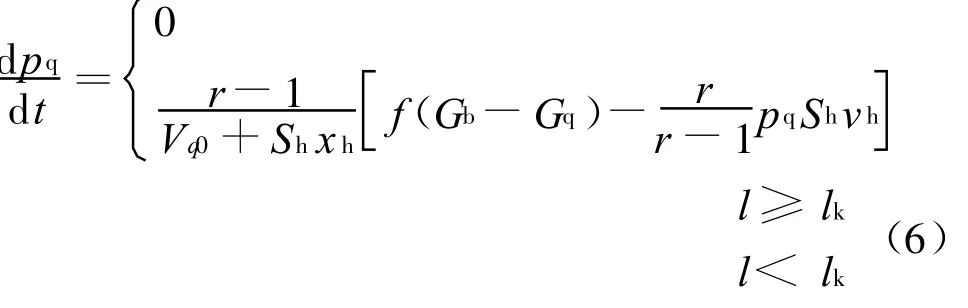
式中:pq为导气室压力;Vq0为导气室初始容积;Sh为导气室活塞横断面面积;vh为导气室活塞运动速度;lk为开孔距离。

2)活塞与自动机运动方程

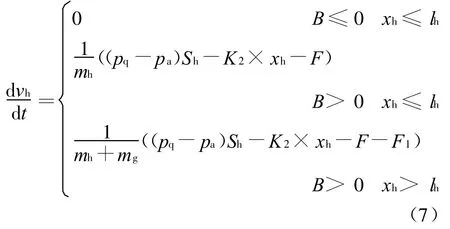
式中:mh为活塞质量;xh为活塞位移;lh为自动机最大运动位移;K2为活塞复进簧刚度;F为随动机构摩擦力和传动阻力;F1=mg(R21-R22)ω2为供弹具转动所需的力;mg为供弹具转动惯量对应的质量;R1为供弹具外径;R2为供弹具内径;ω为平均角速度;B=(pq-pa)Sh-K2×xh-F为活塞所受到的合力。

3)从枪管流入导气室的火药气体流量

4)活塞间隙的流量方程同文献[11]中方程(17-18)。

5)气室内气体质量变化速度方程同文献[12]中方程(17-17)。

6)活塞运动位移方程同文献[11]中方程(17-22)。

7)气室内气流质量守恒方程同文献[12]中方程(8.3.4)。

8)气室内单位质量气体的比内能方程同文献[11]中方程(17-16)。

2.4 耦合方程

内弹道过程与自动机的耦合方程同文献[11]中方程(8.3.12)。

3 实例

3.1 模型验证

为了验证本文所建模型的正确性。将文献[9]中的计算原始数据代入本文所建立的模型,得出如图2所示的计算压力曲线对比图。

从图2中可以看出,在起始阶段本文的计算压力都偏小,中后期压力一致性相对较好,而且关键点的数值差别不大,考虑到本文建立模型时未考虑液体火药雾化燃烧等微观过程,计算结果与文献[9]的计算结果一致性较好。文献[9]指出:虽然其计算的压力曲线与实测压力曲线存在差异,考虑到所建模型作了部分简化,其计算模型还是基本上可以描述内弹道过程的宏观过程。从而表明本文建立的再生式液体发射药自动武器理论计算模型是正确可靠的。

3.2 某型液体发射自动武器性能计算

本文概念设计了某液体发射的导气式自动武器,根据其结构诸元和装填条件,利用所建的理论模型对其相关内弹道参数进行数值求解,采用四阶龙格库塔法,通过MAT LAB编程实现。通过理论计算,得到该型自动武器的膛内压力和储液室压力随时间变化曲线和液体火药喷射速度随时间变化曲线如图3、图4所示。

在起始阶段,燃烧室和储液室处于压力静平衡状态,随着燃烧室压力增大,储液室压力也随之上升,由于截面积的差异,储液室压力上升的加速度要快于燃烧室,从而在储液室和燃烧室之间形成一个压力差,当压力差达到一定的阀值,液体火药开始从储液室喷入燃烧室开始燃烧,此时喷入的流速相对较低,随着喷入的液体火药在燃烧室内燃烧,压力迅速增大,储液室和燃烧室之间的压力差会瞬间增大,从而导致喷入燃烧室火药的速度急剧增加,从图3中可以看出,当液体火药喷射完毕时,压力之差最大达到90 MPa,此时,流速已达到346 m·s-1最大速度,图4中前期,流速出现震荡,这主要是在起始阶段参数匹配原因引起的[7]。

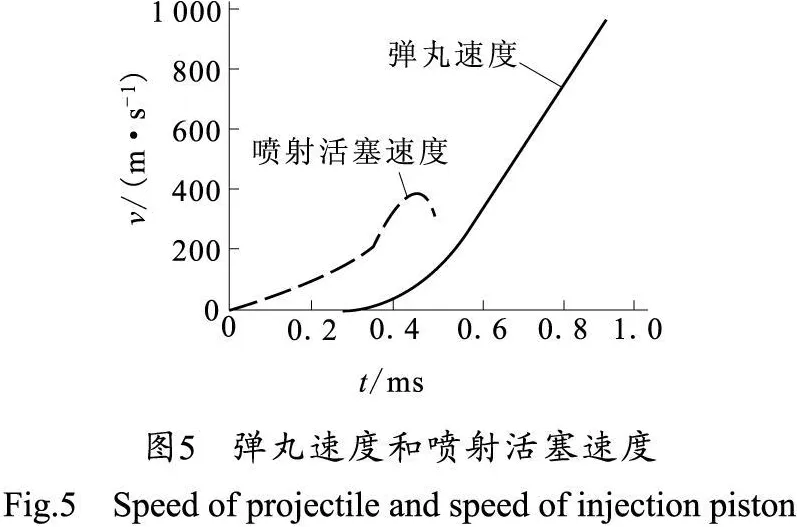
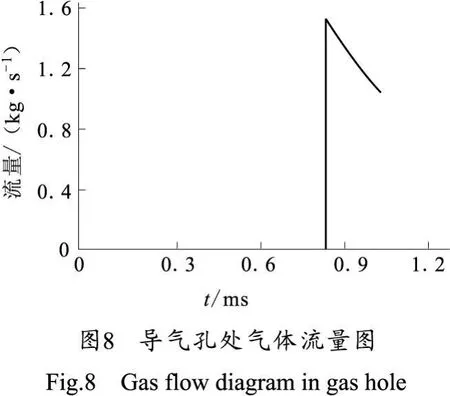
由于点火药的燃烧,燃烧室和储液室的压力平衡被打破,活塞的速度逐渐增大(如图5所示),液体火药受到压缩,密度随之增大(如图6所示),但是由于储液室和燃烧室的压力之差尚未达到喷射的启动压力,储液室的液体火药没有喷射到燃烧室,直到0.23 ms,达到喷射的启动压力,火药喷射的百分比才逐步升高,在0.75 ms左右喷射完毕(如图7所示)。由于弹丸向前运动,燃烧室压力迅速减小,储液室的压力随之迅速上升,当储液室压力与燃烧室的压力在0.42 ms重新使活塞达到平衡状态,随后,弹后空间进一步最大,燃烧室与储液室出现压力之差减小,活塞作减速运动,直到液体火药武器喷射完毕。如图8所示,当弹丸位移小于开孔距离时,导气孔处的气体流量为零,导气室的压力为一个大气压(如图9所示),当弹丸到达导气孔时,膛内压力很大,而导气室内压力仅为一个大气压,从而在导气孔处出现正向临界流,流量在瞬间达到1.48 kg·s-1,导气室的压力在 0.03 ms达到最高的26.8 MPa,在导气室高温高压火药的作用下,导气活塞加速后坐,使得导气室空间进一步增大,导气室压力逐渐减小,造成导气室压力与膛内压力之差也迅速减小,进而使得流量也随之下降,直到弹丸飞出枪口。

3.3 参数对液体发射自动武器内弹道性能的影响

3.3.1 喷孔面积对膛内压力和储液室压力的影响

从图10、图11可以看出,当喷孔面积增加,膛内压力和储液室压力随之增大,且喷孔面积在越小的数值范围变化时,膛内压力和储液室压力的变化越敏感,随着面积增大,敏感度随之降低,但总体来讲,膛内压力和储液室压力受开孔面积影响较大。从图11看出,随着喷孔面积的增加,液体火药喷射完毕的时间越短,储液室最大压力达到的时间越短。

3.3.2 储液室面积对膛内压力和储液室压力的影响

从图12、图13可以看出,随着储液室面积的增大,膛内压力和储液室压力都随之增加。储液室面积在越小的数值范围变化时,膛内压力和储液室压力的变化越敏感,储液室面积在较大范围变化时,这种敏感度会随之降低。相对而言,膛内压力对储液室截面积更为敏感。从图13看出,随着储液室面积的减少,储液室最大压力达到的时间越短。

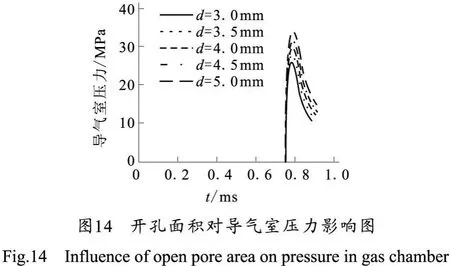
3.3.3 导气孔直径对自动机的影响

从图14、图15可以看出,随着开孔面积的增加,导气室压力和自动机后坐速度都随之增大。导气孔面积增大,导气室压力和自动机后坐速度随之增大,当导气孔面积在较大值范围变化时,导气室压力和自动机后坐速度变化较为敏感,随着开孔面积的减小,这种敏感度随之降低。

4 结束语

提出了一种基于再生式液体发射技术的导气式自动武器的概念模型,阐述了其发射过程,并建立了能够全面真实反映其内弹道的变质量热力学发射过程的零维数学模型,采用对比的方法,利用文献[9]的研究成果验证了该计算模型的正确性。该模型能全面真实地反映基于再生式液体发射技术的导气式自动武器的发射过程,比较适合工程应用。特别是它在自动武器性能的精细化预测方面具有优势,除此之外,该模型为基于再生式液体发射药的导气式自动武器虚拟样机动力学仿真提供了一种载荷添加方法,所以,该模型具有理论和实用价值。利用该模型,探讨了结构参数对其内弹道特性的影响,得出了其影响的基本规律。

References)

[1]金志明,翁春生.高等内弹道学[M].北京:高等教育出版社,2003:312-386.

JIN Zhi-ming,WENG Chun-sheng.Advanced interior ballistics[M].Beijing:The High Education Press,2003:312-386.(in Chinese)

[2]栗保明,金志明.再生式液体发射药火炮中雾化燃烧过程的模拟[J].弹道学报,1994,12(4):12-17.

LI Bao-ming,Jin Zhi-ming.Simulation of jet atomization and combustion in regenerative liquid propellant guns[J].Journal of Ballistics,1994,12(4):12-17(in Chinese)

[3]刘俊,余永刚,周彦煌.再生式液体发射药火炮的雾化问题研究[J].火炮发射与控制学报,2002(3):56-60.

LIU Jun,YU Yong-gang ZHOU Yan-huang.Study of atomization in regenerative liquid propellant gun[J].Journal of Gun Launch&Control,2002(3):56-60.(in Chinese)

[4] JOHN MANDZY.Weapon system implications of RLPG technology[R].ARL-CR-446,2000:1-93.

[5]王亮宽,张相炎,刘宁.再生式液体发射药火炮贮液室激波模型[J].兵工学报,2007,28(8):915-918.

WANG Liang-kuan,ZHANG Xiang-yan,LIU Ning.Shock wave model in reservoir of regenerative liquid propellant gun[J].ACTA Armamentarii,2007,28(8):915-918.(in Chinese)

[6]王亮宽.再生式液体发射药火炮压力振荡机理及抑制措施研究[D].南京:南京理工大学,2007:1-11.

WANG Liang-kuan,Study on pressureoscillation mechanism and suppression measure of regenerative liquid propellant gun[D].Nanjing:Nanjing University of Science and Technology,2007:1-11.(in Chinese)

[7]刘宁.再生式液体发射药火炮喷雾燃烧理论及数值模拟研究[D].南京:南京理工大学,2008:1-56.

LIU Ning.Theory and numerical simulation of spray combustion process in regenerative liquid propellant gun[D].Nanjing:Nanjing University of Science and Technology,2008:1-56.(in Chinese)

[8]COFFEE T P.Process in modeling pressure oscillations in regenerative liquid propellant guns[J].Journal of Propulsion and Power,2000,16(2):302-308.

[9]张旭翔,樊文欣,王明丁.再生式液体发射药枪设计与弹道计算[J].弹道学报,1995,7(2):15-20.

ZHANG Xu-xiang,FAN Wen-xin,WANG Ming-ding.The design and interior ballistic calculation of the regenerative liquid propellant gun[J]Journal of Ballistics,1995,7(2):15-20(in Chinese)

[10]张旭翔,王明丁,樊文欣,等.再生式液体发射药枪弹道结果分析[J].弹道学报,1995,7(3):19-23.

ZHANG Xu-xiang,WANG Ming-ding,FAN Wenxin,et al.The interior ballistic result analyses of the regenerative liquid propellant gun[J].Journalof Ballistics,1995,7(3):19-23.(in Chinese)

[11]陆家鹏.自动武器学气体动力学分册[M].北京:国防工业出版社,1988:456-464.

LU Jia-peng.Gas dynamics ofautomatic weapon[M].Beijing:NationalDefense Inclustry Press,1988:456-464.(in Chinese)

[12]廖振强,王涛,余世海.武器气体动力学数值计算方法[M].北京:国防工业出版社,1988:221-228.

LIAO Zhen-qiang,WANG Tao,YUE Shi-hai.The calculation method of gas dynamics of weapon[M].Beijing:National Defense Inclustry Press,1988:221-228.(in Chinese)

Research on Theoretic Model and Parameter Influence Law of Regenerative Liquid Propellant Automatic Weapon

RAN Jing-lu,XU Cheng,WANG Bing

(Mechanical Engineering College,Nanjing University of Science and Technology,Nanjing 210094,Jiangsu,China)

Along with the application possibility of liquid propellant technology in automatic weapon becomes more and more increasing,a kind of concept model of gas-operated automatic weapon based on regenerative liquid propellant technology was put forward,and the zero dimension mathematical model that can totally and really reflect interior ballistic procedure was established.This model includes fluid reservoir control equation,interior ballistic equation,gas-operated device and automatic mechanism motion equation andcoupling equation.Research results acquired from the references was used to verify the correctness of this model.The influence of structure parameter on the interior ballistic features was discussed with the aid of the model,and the basic influence law was obtained.The model has theory and utility value for developing gas-operated automatic weapon based on regenerative liquid propellant technology.

mechanics;liquid propellant;regenerative liquid propellant;automatic weapon;interior ballistics

TJ3

A

1673-6524(2010)04-0001-06

2010-06-09;

2010-07-22

冉景禄(1981-),男,博士研究生,主要从事特种机械设计与优化研究。E-mail:my qunguliang@163.com