单纯形的代数思维
2017-08-14许宁
许 宁
(南京政治学院 基础部,江苏 南京 21003)
单纯形的代数思维
许 宁
(南京政治学院 基础部,江苏 南京 21003)
以单纯形的代数特征为切入点,建立基于矩阵的单纯形手工计算方法,揭示了单纯形及其各种计算技巧之间的内部联系,理清了单纯形由解特殊问题到解一般问题发展路径.
单纯形;单纯形矩阵;两阶段法;大M法
美国运筹学家Frederick S. Hillier 认为:线性规划理论是20世纪中叶最重要的科学进步之一[1],线性规划的一个有效的求解方法是单纯形. 目前对单纯形处理通常是从几何直观开始,借助于单纯形表来展开,或者直接借助于MATLAB软件的linprog函数来求解等等,这些没有体现单纯形思想的精髓,没能体现在一堆数据中通过什么角度的观察,找到最优解的思维过程,不利于培养运用大数据的能力. 本文力图设计一种模式,充分揭示单纯形的代数思维过程,真正理解单纯形的本质.
1 单纯形是什么
现今大部分书籍是通过两个变量线性规划问题的图解法来说明最优值是在凸集的顶点上取得,因而只要比较凸集顶点的目标函数值的大小即可得最优解与最优值,这不能揭示单纯形是什么. 事实上,单纯形本质上是一个迭代算法,我们可以通过下面的例子[2]来考察单纯形是如何工作的. 设


单纯形是这样开始工作的,首先它从方程(2)的一个解(x1, x2, x3, x4, x5, x6)出发,寻找一个满足重复这一过程,直到不能改变目标函数值为止,这最后的解即为最优解.
为此,需要一个初始解(x1,L,x6). 一个简便的方法是令方程(2)中原变量x1=0,x2=0,x3=0,则得松弛变量x4=5,x5=11,x6=8, 目标函数值为 0. 由目标函数

知,当变量x1, x2, x3中至少有一个从零递增时,目标函数值 z 将增加,故解(x1, x2, x3, x4, x5, x6)= (0,0,0,5,11,8)不是最优解. 又(3)中x1, x2, x3前面的系数分别为 5,4,3,故当x1增长时,目标函数值 z 增长较快,为计算简单,只考虑x1增大时情形(x2=x3=0), 此时松弛变量将改变,由松弛变量的非负性知,x1的增长将有一个限制.事实上,把x2=0,x3=0代入方程(2),结合x4, x5, x6的非负性得即x增长1的上界为从而得新解为

对应的目标函数值为25/2,于是(4)是我们需要的新解,但如何在此基础上进一步寻找新解呢?这召唤我们需要一个标准的求新解的方法,回想刚开始我们是利用(x1, x2, x3)=(0,0,0)代入方程(2)得到初始解的,即用为零的变量x1, x2, x3来表示其它的变量,现在新解中(x2, x3, x4)=(0,0,0), 因而要用变量x2, x3, x4来表示目标函数z和变量x1, x5, x6. 事实上,由于为零的量只是x1换成了x4,于是在方程(2)中,由x4=5−2x1−3x2−x3得

把(5)式代入(2)中的z, x5, x6,则方程(2)转化为

显然,目前的解(4)是令(x2, x3, x4)=(0,0,0),代入方程(7)得到的. 由目标函数(6)知,当增加x2, x4时,z值会减少,若仅x3增加时,z 值会变大,故解(4)不是最优解. 类似地,x3不能无限制地增加,因为由方程(7)知,当x3增加时,会导致变量x1, x6值减小,把x2=0,x4=0代入(7),结合x1, x6的非负性有0≤x3≤1.故x3增长的上界为x3=1. 于是把(x2, x3, x4)=(0,1,0)代入方程(7)得新解

此时的目标函数值为13. 因为新解(8)中(x2, x4, x6)=(0,0,0),故要用变量x2, x4, x6来表示z, x1, x3, x5.又(x2, x4, x6)=(0,0,0)是由(x2, x3, x4)=(0,0,0)中把x3换为x6得到的,于是在方程(7)中,由

把(9)代入方程(7)中的其他式子,消去x3得

由于目标函数(10)中变量x2, x4, x6的系数皆为负数,于是当它们至少有一个变量增加时,目标函数值将会减少,故(x1, x2, x3, x4, x5, x6)=(2,0,1,0,1,0)是最优解,其最优值为z=13.
刚才在求新解的过程中,有些变量令他为零,另一些变量自由增长,这就需要把这些决策变量进行分类,由此引入所谓的线性规划标准形、基变量、非基变量、入基变量、出基变量等概念.
上述分析知,单纯形是从初始点X0=(0,0,0,5,11,8)走到了新的点接着从X1出发,继续寻找使的新解X2,其方法与求解X1类似,即在原基变量指标集B与非基变量指标集N基础上,结合目标函数(6)确定入基变量和出基变量,形成新的基变量与非基变量的指标集B,N,利用新的非基变量,结合方程(9)来改写目标函数方程(6)与方程(7),得到新的方程(10),(11),令非基变量为 0 代入新方程,可得新解X2, 如始重复,直到新的目标函数表达式中,决策变量的系皆为非正数,终止,则最后得到的解即为最优解. 这就是单纯形法.
2 单纯形的手工计算技术
要进一步把单纯形从感性认识提升到理性认识,需要一个简洁的方法来展现单纯形的计算过程. 现有的材料中,单纯形计算是通过所谓的单纯形表来展现的,这不利于大众掌握单纯形的实质,造成理解的困难,一个重要原因是计算手段不自然,不能充分体现单纯形的迭代思想,为此,需开发新的计算表现工具.事实上,由于单纯形的迭代本质上是解线性方程组,于是借助于方程组的矩阵表示方法能很好地展现单纯形的计算过程,我们把单纯形表用单纯形矩阵来表示. 下面借助问题(1)的求解过程来说明这一单纯形求解技术. 为表述方便,我们作如下规定:单纯形矩阵由变量行、基变量列、方程的增广矩阵组成,增广矩阵的上边一行为变量行,按z, x1, x2,L,x6, b顺序书写,其中 b 表示常数项,z 表示目标函数值,x1,L,x6为决策变量. 增广矩阵的左侧列为基变量列,该列中第一个分量写z,其位置对应目标函数方程的系数行,第2至第4个分量为基变量,其位置分别对应于它们所在方程的系数行. 增广矩阵中,除去第一行(目标函数系数行)、最后一列(常数项列),子单位阵的列向量所对应的变量为基变量. 增广矩阵的右侧列是计算比值列.
事实上,若把规划问题( 2)改写为

则结合方程(12)式知,规划问题(2)的初始单纯形矩阵为

其中子单位阵每列所对应的变量为x4, x5, x6(称为基变量),放在增广矩阵的左侧列.
下面的计算中,按单纯形的迭代步骤,从一个矩阵到下一个矩阵,之间用箭线连接,箭线上的“a×(i)+(j )”表示把第i行乘数a后加到第j 行,“a×(i)” 表示把第i行乘数a,[b]表示数b是主元. 单纯形的迭代步骤是:(1)入基变量: 在单纯形矩阵的第1行中,选择决策变量负系数中最小的数的列所对应的变量作为入基变量. 称这个系数所在的列为枢轴列;(2)出基变量: 首先找出枢轴列中每一个严格为正的系数,用这些系数除以同一行的常数项,写到同一行常数项的右侧,其次找出比值最小的行,该行称为枢轴行,该行上的基变量即为出基变量;(3)主元:同时在枢轴行与枢轴列的数字称为主元;(4)换基:在基变量列中,把出基变量换为入基变量,同时将主元化为1;(5)消元:主元的同列其他元素化为0. 具体表述如下

矩阵(14)称为最优单纯形矩阵(增广矩阵的第一行决策变量的系数皆非负),由(14)知,该规划问题的最优值为13,最优解为(x1, x2, x3, x4, x5, x6)=(2,0,1,0,1,0).故原问题的最优值为13,最优解为(x1, x2, x3)=(2,0,1).这就是单纯形的手工计算方法.
上述表明,单纯形是一迭代运算,它从初始单纯形的矩阵开始,找主元、换基、消元,完成第一次迭代,然后从新的单纯形矩阵开始,找主元、换基、消元,完成第二次迭代,如此反复直到得出最优矩阵结束. 那么,为什么用单纯形得到的结论一定是规划问题的最优值和最优解?这就要探索单纯形的数学原理. 事实上,若线性规划标准形有可行解,则一定有基可行解;若线性规划标准形有最优解,则一定有最优基可行解[3]. 若单纯形矩阵中第一行决策变量的系皆非负,则由该矩阵表示的线性方程组决定的基可行解是最优解[4].
3 单纯形运用中的技巧
单纯形是在给出一个初始的基可行解的基础上,按照一定的规则进行迭代,求出最优解. 实际操作中,要使单纯形发挥作用,约束条件(m个)构成的方程组中要有一个明显的子单位矩阵(m×m阶). 拿约束条件为小于等于的线性规划问题来说,我们引入松弛变量,从而在单纯形初始矩阵中有一个子单位矩阵,故可把松弛变量作为初始基变量,令所有非基变量为零,则每个基变量等于它所在方程的非负常数项,这就确定了初始基可行解. 但现实中的线性规划问题通常不具备这样的标准形式,从而导致初始基可行解不容易确定. 为此需要做特别的处理,其中一个标准的方法是人工变量法. 该方法是通过对每个需要的约束条件引入一个虚拟变量(称为人工变量),构建一个更为简便的人工问题. 引进这个变量只是为了使该方程出现初始基变量. 比如一个线性规划问题的约束条件为

为了求(15)的一个可行解,引入人工变量x4≥0,x5≥0,考察如下的极小化问题

显然,若(15)有可行解,则(16),(17)的极小值为0,此时(x4, x5)=(0,0). 若(15)无可行解,则(16),(17)的极小值大于0.
(16),(17)是典型的线性规划标准形,显然,(x1, x2, x3, x4, x5)=(0,0,0,4,3)是一基本可行解,故可用单纯形求最优解. 若(16),(17)的极小值是0,则最优解中(x4, x5)=(0,0),从而最优解中的(x1, x2, x3)的值是(15)的一个可行解. 事实上,(16),(17)的规划问题的初始单纯形矩阵为
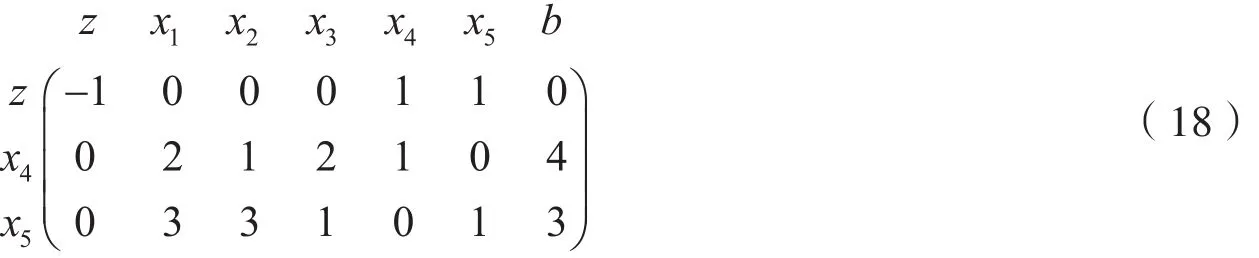
由于单纯形的搜索路径是从目标函数非基变量的系数大小的比较开始的,且目标函数中没有基变量,于是在矩阵(18)中运用初等行变换,把第一行的基变量对应的系数化为零,即

矩阵(19)中的第一行具备了单纯形开始搜索的条件. 此时单纯形开始了找主元、换基、消元的搜索过程.如此反复直到得到最优矩阵为止. (19)的最优矩阵为


在(20)中去掉人工变量x4, x5对应的两列元素,同时把第一行的目标函数的系数换用(21)的目标函数系数代替(注意要把min z转化为max(-z)),则得(21),(15)的初始单纯形矩阵由于(22)第一行中基变量x1, x3的系数非零,于是要把第一行中的基变量的系数化为零,这样单纯形才能发挥作用. 事实上


(23)是最优单纯形矩阵,因而问题(21)(15)的最优解为的极小值为这就是所谓的两阶段法.
从上面分析知:两阶段法的第一阶段是解决约束条件含有“=,≥或常数项为负”等形式带来的如何确定初始的基可行解的问题,第二阶段是在基可行解的基础上结合原问题的目标函数再次运用单纯形迭代可得结论. 对于这样类似的约束条件的线性规划问题,我们也可以用统一的方法来进行处理,这就是大M法,限于篇幅,这里略去.
4 单纯形的智能化
单纯形法可用来解决大型的线性规划问题,这些问题通常有上千个约束条件和更多的决策变量,实践表明,它已成功解决的问题有几十万个约束条件和几百万个决策变量. 显然,手工计算是不能解决这样大型的问题,这必然要求把单纯形用计算机编码来实现,事实上,人们已开发了许多包含单纯形的规划软件包,如Excel Solver,LINDO(LINGO),CPLEX,MATLAB等. 目前CPLEX11已成功地求解了工业中产生的有几千万个约束条件和决策变量的线性规划问题[5]. 在实际工作中,人们常用MATLAB来解决问题. MATLAB的单纯形的求解工具是 linprog函数. 只要按照linprog的语言规则输入,即可得到结论. 比如问题(1)的MATLAB代码如下:
5 结语
随着计算机的广泛应用,人们可能永远不再需要用手工去求解线性规划模型,从而导致只需学会输入数据的机械模式.这种模式回避了在模型求解时,计算技术遇到哪些困难,人们是如何克服的种种认识.没有对前人在困难面前如何寻找突破口的感悟,后人的创新就很难实现,这不利于人才的培养. 同时,单纯形的表格式的计算技术,没有融入人的思维过程,也不利于接收,再者,单纯形计算中的多种技术的展现,扰乱了人们的眼界,没有反映出思维的主线是什么,以及各种计算技术之间的内在联系.
针对这一现象,我们首先给出单纯形是什么,让人们有一个初步的映象,接着开发一种融入人的思维习惯的单纯形的求解技术,避免烦琐的计算淹没对单纯形本质的人识,在此基础上,指出单纯形的代数特征,即在初始单纯形矩阵中含有与约束条件个数一致阶数的子单位矩阵,然后寻找解决一般问题中如何构建这样的子单位矩阵,这样很自然地引入两阶段法和大 M 法,这就是所谓单纯形的技巧. 最后,介绍如何利用计算机来展现单纯形的操作过程. 从而在实际工作中,提升了自觉地应用单纯形来解决实际问题的能力.
[1]HILLIER F S. Introduction to Operations Research [M].9th ed. 北京:清华大学出版社, 2010:25-46.
[2]VANDERBEI R J. Linear Programming: Foundations and Extensions [M].2th ed. New York: Springer, 2002: 13.
[3]LUENBERGER D G. Linear and Nonlinear Programming [M]. 3th ed. New York: Springer,2008: 20-22.
[4]DANTZIG G B. Linear Programming and Extensions [M]. California: The Rand Corparation,1963: 94-100.
[5] BIXBY R E. Solving Real-World Linear Programs: A Decade and More of Progress[J]. Operations Research, 2002,50(1):3-15.
Abstract:According to an algebraic characteristic for simplex, in this paper, a new method is established based on matrix for manual calculation of simplex, and the internal connection between the simplex and its computational techniques is revealed, elaborating the development path from special to general for simplex.
Key words:simplex; simplex matrix; two-phase methods; big-M method
On the Simplex Algebraic Thinking
XU Ning
(Department of Basic Courses, Nanjing Political College, Nanjing 21003, China)
O221.1
A
1008-2794(2017)04-00114-08
2017-02-24
许宁,教授,博士,研究方向:偏微分方程、军事运筹学,E-mail: xuningnj@163.com.
