基于C-W制导的瞄准点修正技术

马艳红，胡 军

（1.北京控制工程研究所，北京100190；2.空间智能控制技术国家级重点实验室，北京100190）

基于C-W制导的瞄准点修正技术

马艳红1，2，胡 军1

（1.北京控制工程研究所，北京100190；2.空间智能控制技术国家级重点实验室，北京100190）

在分析C-W冲量制导误差源的基础上，指出主要摄动为C-W方程的线性化误差，相对J2项摄动误差和发动机的冲量假设误差.在求解得到主要摄动作用下相对运动方程解析解的基础上，提出了瞄准点修正技术，在计算量增加不大的前提下，不仅提高了C-W制导精度，而且实际制导曲线趋近于最优交会轨迹，燃料消耗接近最优解.

C-W制导；J2项摄动；瞄准点

在交会对接中，当目标器轨道为近圆轨道，且追踪器距离目标器较近时，相对运动可采用Hill方程描述，其时间解的形式通常称为C-W方程.Hill方程为线性方程，以此为基础求解制导律算法简单，因此在交会对接中得到广泛应用，称为“Hill制导”或“C-W制导”.

在实际应用中，由于各种误差的存在，C-W制导无法将追踪器沿优化轨迹导引到理想位置，需要进行修正.对制导轨迹进行修正有两种方法：1）在优化轨迹附近设计一容许误差带，超出该范围则进行修正机动；2）在制导算法中对各种误差进行估计和补偿，使得实际制导曲线趋近于优化轨迹.方法一的缺点是需要增加修正冲量，增大了燃料消耗；方法二节省了燃料消耗，但是需要高效的修正算法.本文以共面近圆轨道交会任务为例，采用方法二，提出基于C-W方程摄动解析解的瞄准点修正技术，在计算量增加不大的前提下有效提高制导精度，且燃料消耗接近最优解.

1 C-W制导误差源分析

相对运动坐标系原点取为目标器质心，y轴指向地心，x轴在轨道平面内指向追踪器方向，z轴垂直于轨道平面.对于共面近圆轨道交会，只考虑轨道平面内的运动，C-W方程如下所示：

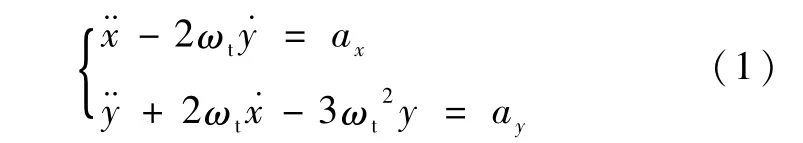
式中，ωt为目标器轨道角速度，a＝［axay］T为摄动加速度，ρ＝［x y］T为追踪器相对目标器的相对位置.

C-W制导时，不考虑环境摄动，并假设发动机推力为冲量，制导误差源［1-2］主要包括以下几个方面：

（1）C-W方程的线性化误差

C-W方程是在两飞行器相对距离较近的情况下，对地球中心引力进行一阶近似得到的线性化方程，线性化过程引入的误差随相对距离的增大而增大.

（2）摄动加速度误差

式（1）中摄动加速度矢量定义如下：

下标c表示“追踪器”，t表示“目标器”，交会过程中假设目标器无发动机推力控制，→a主要包括追踪器发动机推力加速度、相对气动摄动加速度和相对J2项摄动加速度.但在制导律求解过程中，通常只考虑发动机推力加速度，由于忽略气动及地球扁率影响而引入的误差称为“摄动加速度误差”.

（3）冲量假设误差

C-W制导律求解中，通常假设发动机推力为冲量形式，而发动机实际推力形式更接近于常值，由此引入的误差称为“冲量假设误差”.控制结束后两航天器的相对运动称为“自由运动”，冲量假设误差主要影响自由运动的初始状态.

此外，导航精度也影响着制导精度，其形式与冲量假设误差的影响一致，都反映在自由运动时的初始状态不同.上述各种误差中，除了导航误差需要提高导航精度才能提高外，其他各种误差均可在算法中对其影响进行估计并补偿，从而提高制导精度.

文献［3］采用数值模型进行积分解算对上述误差进行估计并补偿，由此引入较大的计算量，不利于在线实现；文献［2］针对主要误差求取解析解，很大程度上提高了求解效率，下面对其求解思路进行简单说明.

1.1 线性化误差作用下相对运动方程的解析解

线性化误差中影响最大的是相对运动参数的二阶项，因此如果采用二阶相对运动方程描述相对运动，则可很大程度上减小相对运动方程线性化误差的影响.早在1963年，London［4］就基于摄动理论给出了二阶相对运动方程解的解析形式；对于共面近圆交会，其轨道平面法线方向上的运动较小，因此此处只考虑轨道平面内的运动和控制，对London的结论进行简化，得到轨道平面内二阶摄动解的解析式［2］.

记rt为目标器的矢径长度，二阶相对运动方程为：

记C-W方程的解为

设相对X1而言二阶摄动解为小量，记

则式（3）的解有如下形式：

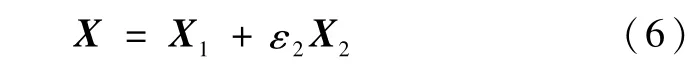
X1可直接得到，忽略ε2X2的高阶项，则由式（3）可得摄动解满足下式：

由于X1可直接求解得到显式表示，则X2可依据下式求解：

设发动机作用结束后系统状态为X（0），此时X2（0）＝0，得到摄动解有如下形式：

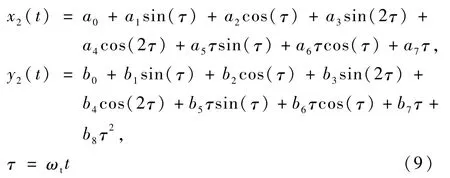
式中ai，bi是X（0）二阶项的线性组合，具体形式参见文献［2］.X（0）的精度取决于相对导航精度，式（9）称为“自由运动时线性化误差的摄动解析解”.

1.2 相对J2项摄动作用下相对运动方程的解析解

摄动加速度误差中影响最大是“相对J2项摄动”，将追踪器所受J2项摄动加速度在目标器参考轨道处取一阶近似，得到相对J2项摄动的解析式如下：

则相对J2项摄动作用下，相对运动方程的摄动解有如下形式：

只考虑轨道平面内的运动，设ε3X3相对X1为小量，并记▽J2t（i，j），i＝1，2，3，j＝1，2，3为矩阵▽J2t第i行第j列元素，则依据式（1）可得

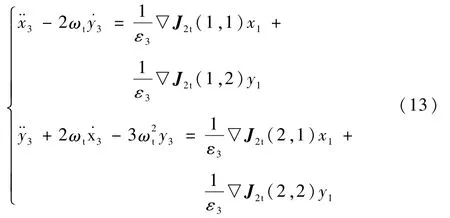
从而X3（0）＝0时，摄动解有如下形式：

其中

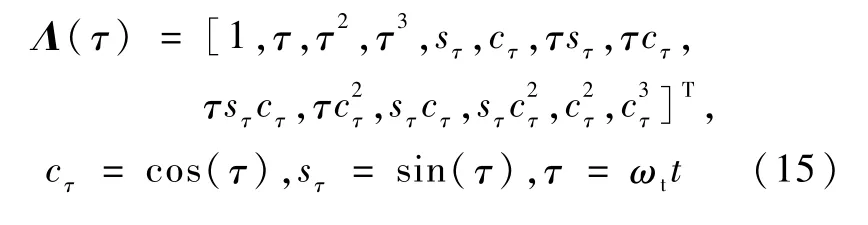
各系数αi，βi是X（0）一阶项和目标器轨道参数的函数，具体形式参见文献［2］.X（0）的精度取决于相对导航精度，式（15）称为“自由运动时相对J2项摄动的摄动解析解”.

1.3 冲量误差的估计

同样的速度增量，控制量为常值推力时和控制量为冲量形式时，得到的自由运动的初始状态不同.C-W制导中假设控制量为冲量得到制导用速度增量，结合发动机推力模型，可求解得到发动机常值推力作用后系统的状态，以此为基础结合自由运动时线性化误差和相对J2项摄动作用下的摄动解析解，可以对C-W制导的误差进行有效估计.

2 瞄准点修正技术

C-W冲量制导优化可得到一条最优交会轨迹使得交会燃料消耗最小，称为“理想轨迹”，该轨迹上的各个冲量作用点称为“理想位置P0”，作用冲量称为“理想冲量”；但是由于各种误差的存在，“理想冲量”作用下无法将追踪器沿着“理想轨迹”导引到“理想位置”，考虑主要摄动时对实际制导位置进行估计，得到“估计位置P′”.

定义“瞄准点”为制导律求解中所采用的“设计位置”，或称为“计算用位置”，记为P*.瞄准点修正的目标是使得针对瞄准点P*设计的制导律，作用后使得实际位置P接近理想位置P0.修正逻辑如图1所示.

图1 瞄准点修正逻辑

在前述推导得到主要摄动作用下摄动解析解的基础上，瞄准点修正变的非常简单，估计位置P′可直接依据下式计算：

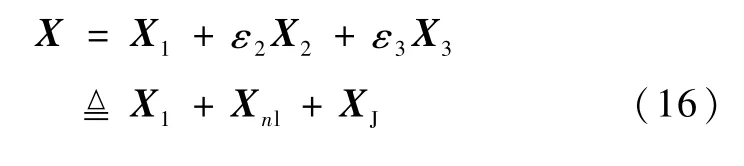
式中，Xnl，XJ分别称为自由运动时线性化误差和相对J2项误差的摄动修正解.记

瞄准点修正中设

瞄准点修正流程图如图2所示.由于在摄动修正过程中进行了多种简化，因此没有必要修正瞄准点使得终端误差估计ΔP′＝0，而是设定误差限使‖ΔP′‖＜σ时输出相应的瞄准点，这种算法收敛迅速，一般经过一两次修正即可满足要求，修正后C-W制导方法可以用于相对距离较远时的制导律求解，而无需增加修正冲量，从而节省了燃料消耗.文献［3］中也采用了瞄准点修正的思路，但在估计位置P′的求取过程中采用数值模型进行积分解算，计算量大，不适合星上在线实现；本文由于采用了主要摄动作用下的摄动解析解，从而计算量较小，适合星上使用.

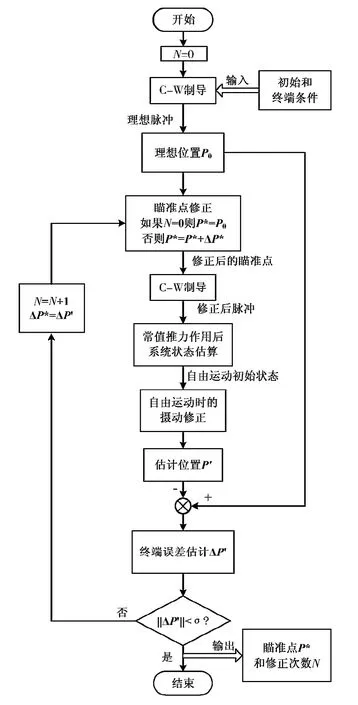
图2 瞄准点修正逻辑

3 仿真算例

假设目标器轨道为450 km的圆轨道，初始时刻追踪器位于距离目标器100 km的共面圆轨道上，轨道高度较目标器低20 km；寻的段要求通过三次机动将追踪器导引到目标器轨道上距离目标器后5 km处的“停泊点”，交会时间为0.7个目标器轨道周期，三次冲量时刻分别为初始时刻t0，停泊时刻tf和0.5tf.采用Lagrange乘子法求解C-W冲量制导，得到理想控制用速度增量（m／s）分别为

则最优燃料消耗（m／s）为

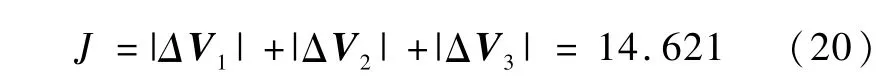
设x轴方向的发动机推力加速度为0.04 m／s2，y轴方向为0.02 m／s2，不考虑导航误差，仿真比较得到不进行瞄准点修正和瞄准点修正后的各性能参数如表1所示，相应的交会曲线如图3所示.可见：采用瞄准点修正技术后，不仅提高了制导精度，而且实际制导曲线趋近于最优交会轨迹，燃料消耗接近最优解，相比较无修正的C-W制导而言，很大程度上节省了燃料消耗.

图3 交会曲线比较

表1 交会性能参数比较

4 结 论

本文在分析CRW制导误差源的基础上，得到主要误差作用下相对运动方程的解析解，以此为基础对制导位置进行估计，在制导律求解中对瞄准点进行修正，不仅提高了制导精度，而且实际制导曲线趋近于最优交会轨迹，燃料消耗接近最优解.

瞄准点修正算法收敛迅速，并且由于采用了摄动解析解，因此在计算量增加不大的前提下，保证了算法在线实现的可能性.此外，摄动解析解相关系数的精度取决于导航精度，因此有效的相对导航信息是瞄准点修正在线实现的前提保障.

［1］ Hiroshi I，Robert H B.Analysis of the targeting error induced by Hill′s guidance［C］.AIAA Guidance，Navigation and Control Conference，Monterey，Aug 1993

［2］ 马艳红.C-W制导误差分析［J］.航天控制待发表

［3］ 李晨光，肖业伦.多脉冲C-W交会的优化方法［J］.宇航学报，2006，27（2）：172-176

［4］ London H S.Second approximation to the solution of the rendezvous equations［J］.AIAA Journal，1963，1（7）：1691-1693

C-WGuidance-Based Aiming Point Correction Technique

MA Yanhong1，2，HU Jun1
（1.Beijing Institute of Control Engineering，Beijing 100190，China；2.National Laboratory of Space Intelligent Control，Beijing 100190，China）

Based on error analysis of the C-Wguidance，the article shows that the main perturbation sources of C-Wimpulse guidance are linearization error，relative J2term perturbation，and impulse assumption error of thrusters.When obtaining the analytic solution of perturbed relativemotion equation，an aiming point modification technique is induced to improve guidance accuracy at limited increase of computational effort，and the actual rendezvous trajectory and the fuel consumption are close to optimal ones.

C-W guidance；J2term perturbation；aiming point

V448.23

A

1674-1579（2009）05-0052-04

2009-03-06

马艳红（1980—），女，山西人，工程师，研究方向为航天器交会对接和姿态控制（e-mail：mayanhong1980＠sina.com）.