利用散射波远场模第P个傅立叶系数重建声波阻尼系数

薛琳娜,管金友

(1.延安大学物理与电子信息学院,陕西延安 716000;2.铜陵学院基础系,安徽铜陵 244000)

利用散射波远场模第P个傅立叶系数重建声波阻尼系数

薛琳娜1,管金友2

(1.延安大学物理与电子信息学院,陕西延安 716000;2.铜陵学院基础系,安徽铜陵 244000)

阐述了利用声波散射远场模Fourier展开的第P个傅立叶系数(声散射远场模的不完全信息),重建声阻抗系数的一种非线性最优化方法.并给出了该方法收敛性的证明,其数值例子说明这种方法的有效性和可行性.

声散射；阻抗系数；P-傅立叶系数；远场模；逼近

1 引言

对声散射理论的研究,基于其在许多工程技术和数学物理领域的广泛应用(医学诊断、无损检测、声纳、地震、潜艇等等),而越来越受到重视;在这方面已有很多文献[3-10]其中文[4-5,8]等利用声散射的远场模反演声阻抗系数,本文就这一问题继续研究,其不同于文[4-5,8]的是仅从声散射的远场模Fourier展开的某一个Fourier系数来逼近声阻抗系数.事实上,远场模是观测角θ的解析函数,其展开式系数的信息应当含有声散射的远场本身的信息;当然,从某一个Fourier系数信息是不大可能恢复其在整个观测域中的全部信息的;从而研究仅从一个Fourier系数的信息来获取声阻抗信息将显得很有意义的.在这个意义上,利用声散射远场模的不完全信息来重建声阻抗系数,将从理论上表明,从声散射的远场模Fourier展开的某个Fourier系数来逼近声阻抗系数是可行的；并建立求解这类反问题的一种非线性最优化模型,并提供算例来表明数值实现的可行性、所建立理论和方法的有效性和实用性.

2 逼近的理论分析

2.1 正散射问题

我们考虑在均匀介质中传播的声波.此声波碰到一个无限长的柱体,设柱体的截面D⊂R2(D为原始物形区域),母线平行于z轴,设入射波为平面波,其中k＞0为波数,α为入射方向角,入射波碰到柱体发生散射.记总场为u=ui+us,us为散射波.总场满足声阻抗条件,正散射问题归结为求u∈C2(R2)∩C(R2D)满足

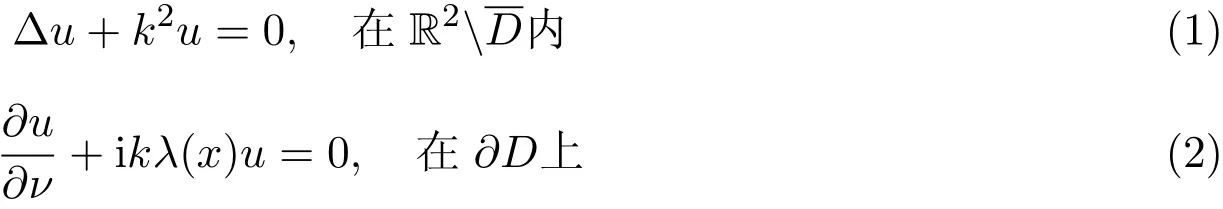
2.2 算子方程的建立

这样就建立了与所求相关的第一类算子方程.

2.3 收敛性分析

因为(18)-(19)式具有光滑核,因而是强不适定的.但当k2不是Γ的Dirichlet特征值时,我们有[2,6-7]:

定理2(19)式是单射,并且F在L2[0,2π]上稠密.

证明若(19)式有解,我们考虑齐次方程Fgp=0,即:存在某个gp∈L2[Γ],使Fgp=0.我们引入单层势

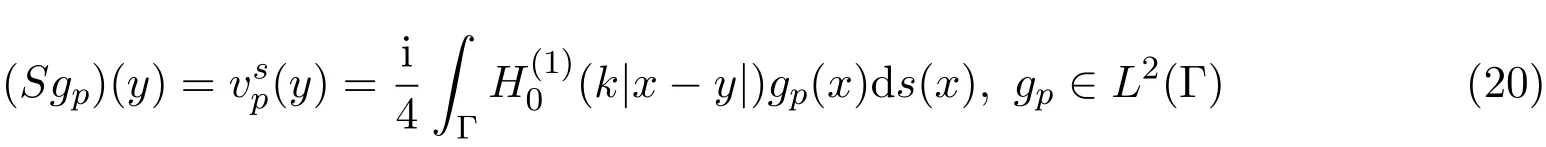
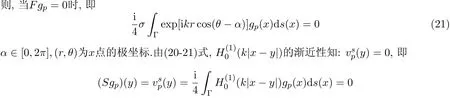
然后由参考文[4]的定理2.1知:S是单射,并在L2[0,2π]中稠密.

满足k2不是Γ的Dirichlet特征值这一条件与Γ的选择有关,因为Γ是事先预作的,因而可以控制,达到k2不是Γ的Dirichlet特征值;然而(19)式满足(15),(16)式的解并不总是存在的,但我们可以证明其在最大模意义下逼近解总可得到.为此我们引入

这样可以定义极小化问题:

首先,用Tikhonov正则化方法求解强不适定方程(19),即:对正则化参数δ＞0,求gp∈L2(Γ),使得

这个极小化问题的解就可作为声阻抗系数λ(x)的一个逼近解.为此定义集合

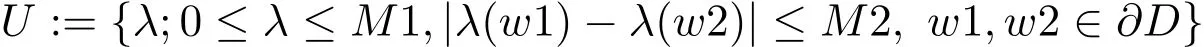
M1,M2是正的常数,由于λ(x)是等度连续的且有界的,由Arzela-Ascoli定理知U是C(∂D)中紧集.将(24)-(25)式结合成一个目标泛函,定义

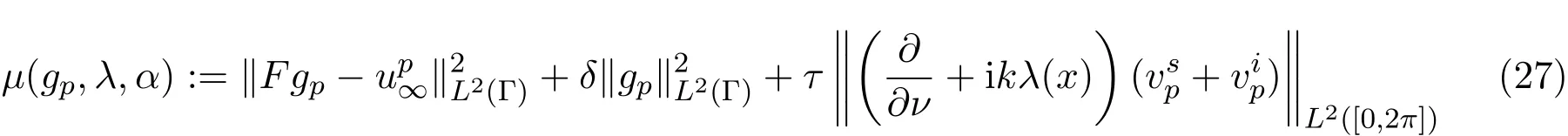
其中,增加的平衡因子τ是用来控制gp的影响,对µ(gp,λ,α)的前面两部分与第三部分起平衡作用.求声阻抗系数即求极小化问题

定义1给定入射波ui对应的远场模式u∞(θ;k,α)的第p个Fourier系数,及固定的正则化参数α＞0,对一个函数λ0,如果存在g0∈L2(Γ),(g0,λ0)使得目标泛函(27)式达到极小,即

下证：λ∗=λ.又因为λn是对应于αn的最优解,即存在gp∈L2(Γ)使得µ(gp,λn,αn)= m(αn),由定理4知

3 数值方法

本节对前面的分析给出算法.假设∂D,Γ围成的物形区域是含有原点的星域.正问题数据参见文[5],然后利用

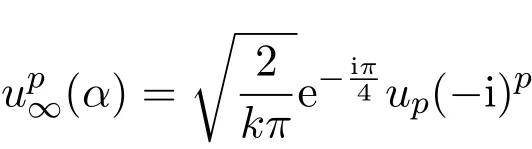
逼近远场模式u∞(θ;k,αn)的Fourier展开的第P个系数.up与文[5]中的正问题的uj意义相同,只不过此处p是j中特定的一个.

反问题是对于给定的波数k和不同方向的N个平面波,其中

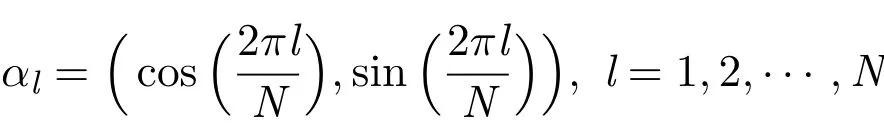
用下面的有限三角级数逼近gp(θ)和λ(x),那么

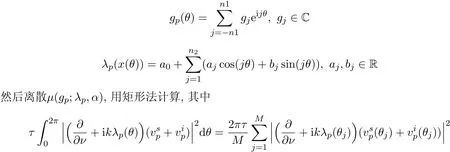
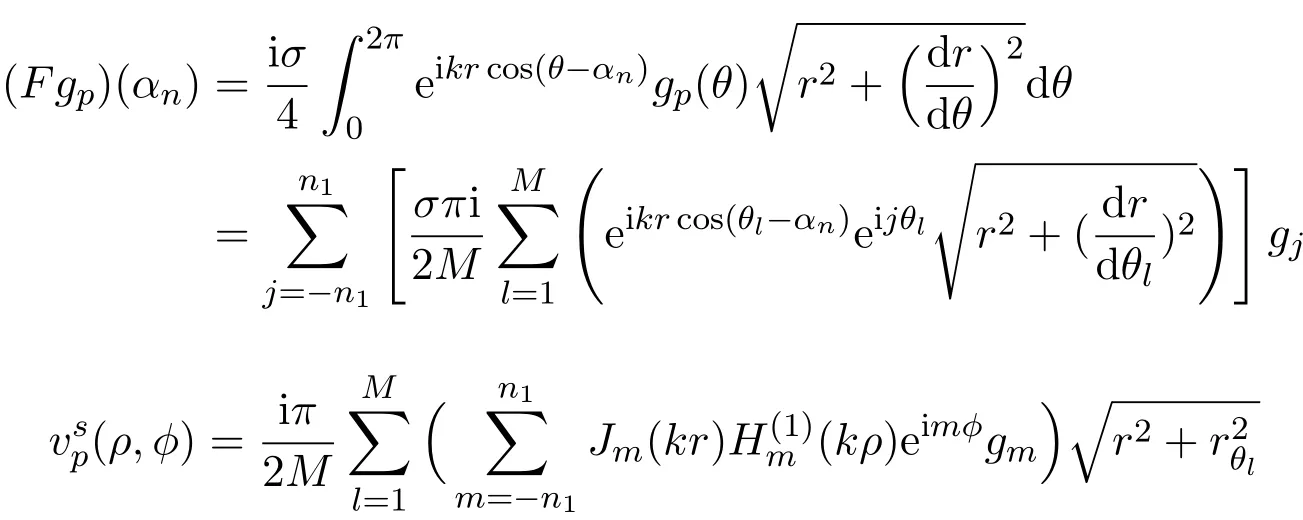
其中τ是平衡参数,rθl是r对θl的导数.以下给出例子.

参数:原始物形区域边界曲线∂D:ρ=1,波数k=1,正则化参数δ=1.0D−10,平衡参数τ=1,入射波数N=13.

正问题:n=6,m=100.反问题:n1=6,n2=6,M=30.

例1原声阻抗系数λ=2+cos3θ+sin3θ

(1)当辅助物形区域边界曲线Γ取r=0.995傅立叶系数p分别取p=0,p=1,p= −1,p=−3时,反演图与原精确图画在同一坐标系中见图1.

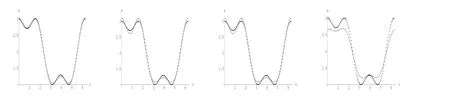
图1 r=0.995时,p=0,p=1,p=-1,p=-3

可以看出越高阶的傅立叶系数逼近越差,这与Hankle函数高阶的傅立叶系数迅速衰减的性质一致,一般傅立叶系数的绝对值大于4时逼近已经很差.

(2)当傅立叶系数p取0,辅助物形区域边界曲线Γ分别取r=0.995,0.95,0.75,0.5时,反演图与原精确图画在同一坐标系中见图2.

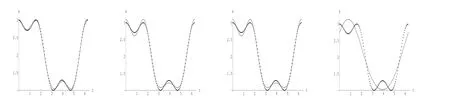
图2 p=0时,r=0.995,r=0.95,r=0.75,r=0.5

可以看出:辅助物形区域越接近原始物形区域,逼近越好.当然,与平衡参数也有关,当辅助物形区域曲线偏离较大时可适当增大平衡参数,本文从略.

(3)下面仅给出p=0,辅助物形区域边界曲线r=0.995时的另外两例:

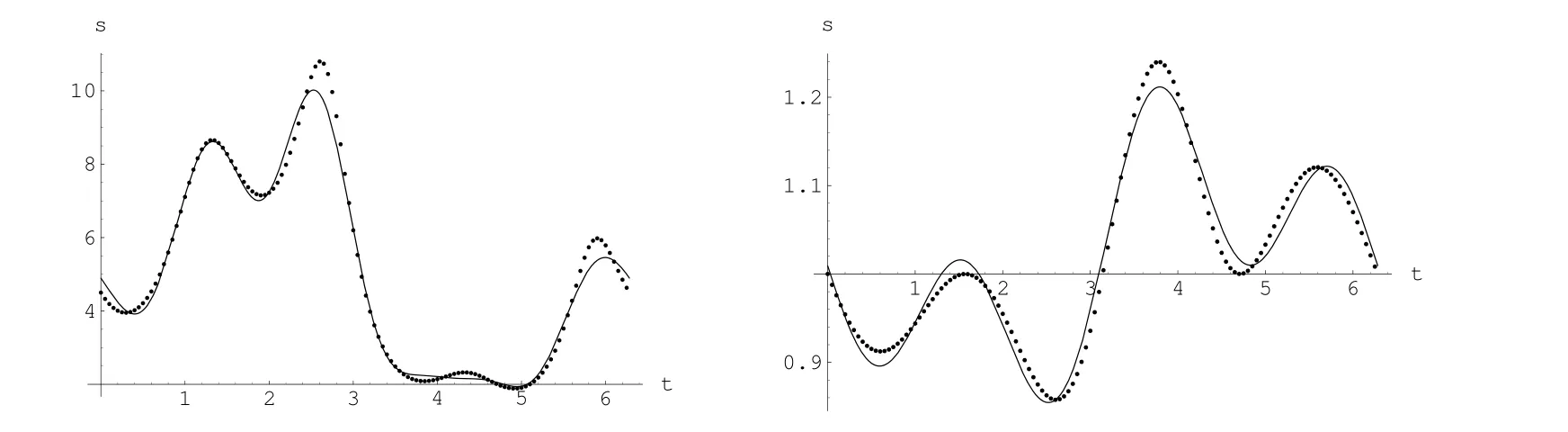
图3 p=0时,r=0.95

此三例的反演结果见表1.

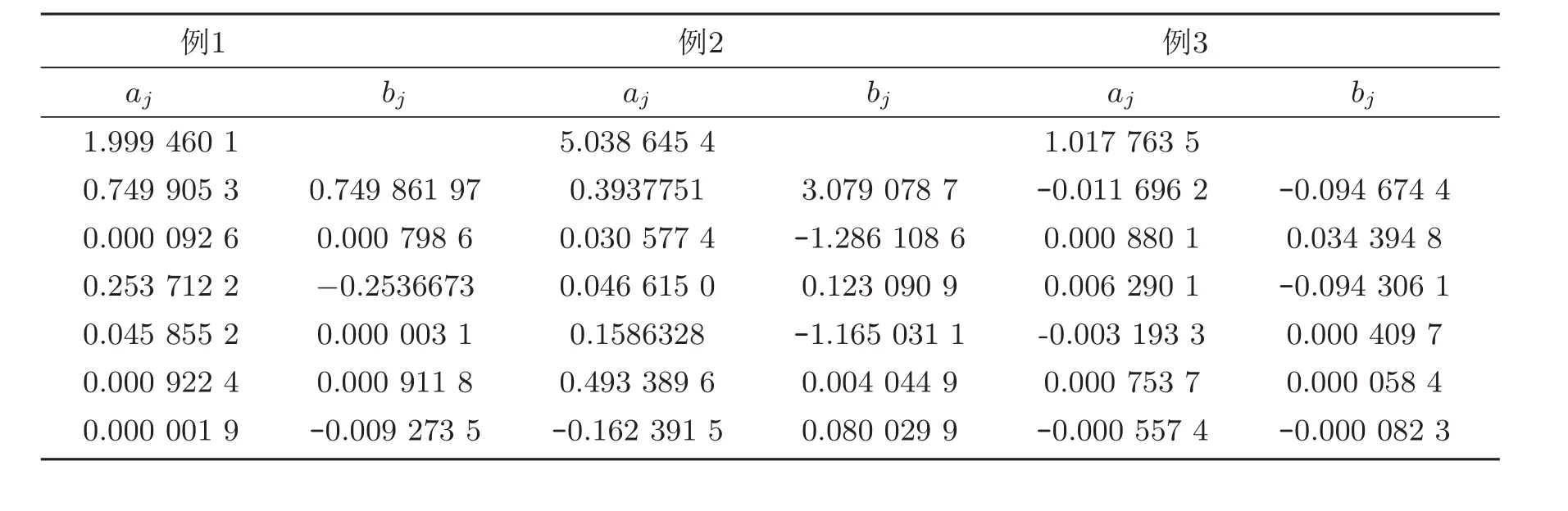
表1 在p=0,r=0.995时的情况

4 结论

利用声散射远场模的不完全信息来重建声阻抗系数或物形,是逆声散射理论的一个具有挑战性的难题,当然也在工程中有较高实用价值.作为在这方面努力的一部分,本文提出了求解阻抗系数的一种非线形最优化算法,从数值结果来看,从声散射的远场模Fourier展开的某个Fourier系数来逼近原声阻抗系数是可能的,但其结果的好坏与Fourier系数的阶数有关,低阶Fourier系数含有的信息量大,逼近较好；同时与辅助物形区域接近原始物形区域的程度有关,越接近原始物形区域,逼近越好.

[1]Cotton D,Kress R.Inverse Acoustic and Electromagnetic Scattering Theory[M].New York:Springer-Verlag Berlin Heidelberg,1992.

[2]Cotton D,Kress R.Integral Equation Method in Scattering Theory[M].New York:Wiley-Interscience Publication,1983.

[3]You Yunxiang,Miao Guoping.Inverse acoustic impedance obstacle problem[J].Acta Physica Sinica,2002,2:270-277.

[4]Wang Liantang.An approximation method for recovering the acoustic wave impedance coefficient[J].Mathematica Numerica Sinica,2000,8:265-274.

[5]Wang Liantang.Recover the acoustic wave impedance coefficient from the far field pattern[J].Mathematica Numerica Sinica,1999,2:89-95.

[6]Cotton D,Monk P.A novel method for solving the inverse scattering problem for time-harmonic acoustic waves in the resonance region[J].SIAM.J.Appl.Math.,1985,45:1039-1053.

[7]Cotton D,Monk P.A novel method for solving the inverse scattering problem for time-harmonic acoustic waves in the resonance region II[J].SIAM.J.Appl.Math.,1986,46:506-523.

[8]Wang Liantang,He Zhiqiang.Recover the acoustic wave impedance coefficient from the incomplete data of the far field pattern[J].Mathematica Numerica Sinica,2003,5:245-256.

[9]You Yunxiang,Miao Guoping.Numerical method for the shape reconstruction of a hard target[J].Applied Mathematics And Mechanics,2003,10:1090-1100.

[10]You Yunxiang,Miao Guoping.A numerical method for solving the shape detection problem[J].Journal of Shanghai Jiaotong university,1997,11:45-50.

[11]王枢,王连堂.反演声波阻尼系数的另一种方法[J].纯粹数学与应用数学,2005,21(4):370-377.

Recover the acoustic wave impedance coefficient from the P-th Fourier coefficient of the far field pattern

XUE Lin-na1,GUAN Jin-you2
(1.College of Physics and Electronic Information,Yanan University,Yanan716000,China; 2.Foundemental Department,Tongling University,Tongling244000,China)

A method is presented for recovering the impedance coefficient given the P-th Fourier coefficient of the far field pattern of the scattered wave.The convergence of this method is proven.Numerical examples are given showing that this method is also accurate.

the scattered acoustic wave,impedance obstacle,P-th Fourier coefficient,the far field pattern, approximation

O178

A

1008-5513(2009)03-0512-09

2006-11-10.

国家自然科学基金(10671155).

薛琳娜(1963-),硕士,研究方向：计算物理.

2000MSC:31A25