长方体上均匀分布的密度函数
2009-07-05陈光曙
陈光曙
(江苏财经职业技术学院,江苏淮安 223003)
长方体上均匀分布的密度函数
陈光曙
(江苏财经职业技术学院,江苏淮安 223003)
讨论了长方体上均匀分布密度函数问题,得到了长方体体积的估计量、估计量的点估计及估计量的密度函数.
估计量;均匀分布;密度函数;长方体
1 引言
均匀分布上概率统计中的重要分布,具有广泛的应用价值.由于随机取的点集被广泛应用于许多概率模型中,如:流行病学、遗传学及交通理论等.因此,均匀分布及其相关统计量的研究也引起了众多学者的关注.如X~U(a,b)(a<b,a,b均为未知参数),设X1,X2,···,Xn是X的简单随机样本,关于参数a,b的估计量,人们更为关注的是它们的极大似然估计量文[1-2]曾研究过参数a,b的估计量的有关性质,并给出许多重要结论,给出了实数a,b的区间估计.文[3-4]进一步研究了一维均匀分布U(a,b)的区间长度L=b−a的估计问题.文[5]在文[3]的基础上,研究了矩形区域上均匀分布的面积估计问题.本文在文[1-5]的基础上,着重研究空间长方体G上服从均匀分布的体积V的估计量ˆV的概率密度函数以及V的点估计问题.
2 有关记号及引理
为叙述方便,引入以下记号和引理:
设G为空间的长方体,G={(x,y,z)|a<x<b,c<y<d,e<z<f},其中a,b,c,d,e,f均为未知参数,V=(b−a)·(d−c)·(f−e)表示G的体积.
设(X,Y,Z)在G上服从均匀分布,记为(X,Y,Z)~U(G),其联合密度为


3 体积V的统计量及其密度函数


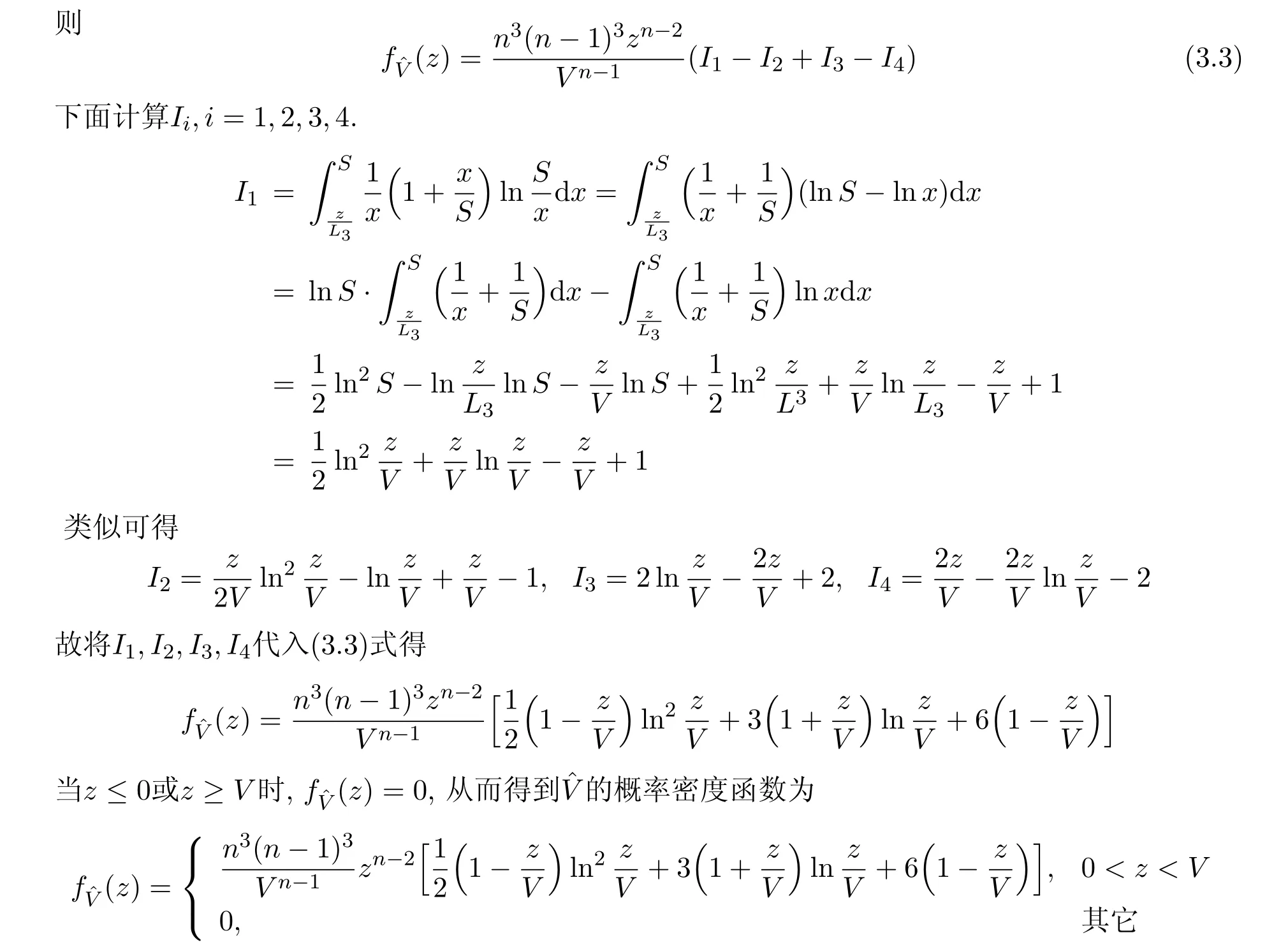
关于体积V的密度函数的性质以及V的区间估计问题,我们将另文讨论.
[1]潘高田,胡军峰.小样本的均匀分布参数的区间估计和假设检验[J].数学的实践与认识,2002,32(4):629-631.
[2]颜贵兴.均匀分布参数的矩估计与最大似然估计[J].广西师院学报:自然科学版,2001,18(2):76-79.
[3]陈光曙.均匀分布区间长度的估计[J].大学数学,2005,21(4):120-124.
[4]陈光曙.均匀分布区间长度估计量的渐近分布及其性质[J].山东师范大学学报,2005,20(3):8-10.
[5]刘兆君.二维均匀分布矩形区域面积的估计[J].大学数学,2007,23(4):155-159.
Density function of uniform distribution on the cuboid
CHEN Guang-shu
(Jiangsu Vocational and Technical College of Finance and Economics,Huaian223003,China)
In this paper,the problem of density function which is in the uniform distribution on the cuboids is discussed.From that,the volume estimator,as well as its point estimate and density function on the cuboids have been given.
estimation,uniform distribution,density function,cuboid
O211.1
A
1008-5513(2009)04-0721-04
2008-02-10.
江苏省高校自然科学基金(05KJD110034).
陈光曙(1961-),教授,研究方向:概率论与数理统计.
2000MSC:60D05
