关于两类含幺幂等元半环

刘伟,胡静,丰丕虎

(西北大学数学系,陕西西安 710127)

关于两类含幺幂等元半环

刘伟,胡静,丰丕虎

(西北大学数学系,陕西西安 710127)

研究了两类重要的含幺幂等元半环簇中成员的一些性质,给出了其中成员的等价刻画,并讨论了其中成员的结构,得到了这两类子簇中成员的一些结果.

幂等元半环；单演双半格；Mal’cev积；簇

1 引言

半环(S,+,…)是指非空集合S上装有两个二元运算“+”和“…”的(2,2)型代数,且满足条件:

(i)(S,+)和(S,…)是半群;

(ii)(∀a,b,c∈S)(a+b)c=ac+bc和c(a+b)=ca+cb.

幂等元半环是指满足附加条件(∀a,b∈S)a+a=aa=a的半环,即(S,+)和(S,…)都是带.幂等元半环簇记为I.

幂等元分配半环是指满足附加条件(∀a,b,c∈S)a+bc=(a+b)(b+c)和bc+a=(b+a)(c+a)的幂等元半环.幂等元分配半环簇记为ID.

单演双半格簇是指满足恒等式xy≈yx,x+y≈y+x,x+y≈xy的幂等元半环的全体,记为M.

若V,W⊆I,V◦W表示半环类{S∈I|(∃ρ∈Con(S))S/ρ∈W,(∀u∈S)ρu∈V},称为V 与W的Mal’cev积.

以下给出与本文相关的三类幂等元半环簇的子簇的记号及其满足的恒等式

有许多文献致力于幂等元半环的研究[14].其中文[1]首先研究了幂等元半环簇的子簇◦D,称其成员为加法带半环,它们是满足恒等式x+xy+x≈x+yx+x≈x的幂等元半环的全体.文[4]运用了偏序关系,Green’s关系等方法研究了幂等元半环簇P的两个重要子簇◦M,◦M的性质,给出了其中成员的等价刻画,并讨论了其中成员的结构.本文将研究文[4]中提到的两类簇中成员在含有幺元素时的性质,等价刻画和结构.

有关半群和范代数的概念和结果可参考文[5-7].

若S∈I,称S为含幺幂等元半环是指:存在e∈S且满足(∀a∈S)ae=ea=a,即(S,…)是幺半群.此时称e为幂等元半环S的幺元素.设X为簇,把X中所有含幺元素的成员组成的簇记为X1.例如:I1表示含幺元素的幂等元半环的全体组成的簇.

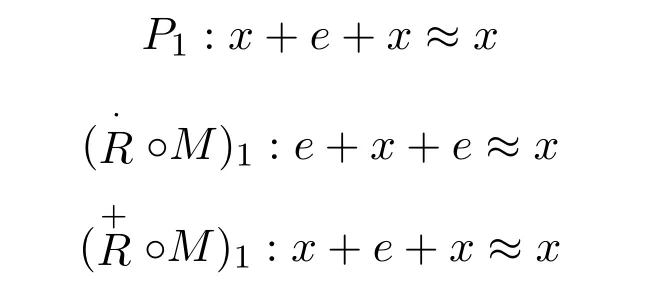
现在考虑上述三类簇中含有幺元素成员的全体组成的簇及相应的恒等式显然P1=(◦M)1,上述三类簇实际上成为两类簇.下面就这两类簇中的成员做一些研究.

2 两类簇中成员的性质

3 两类簇中成员的结构

[1]Sen M K,Guo Y Q,Shum K P.A class of idem potent sem irings[J].Sem igroup Forum,2000,60:315-369.

[2]Zhao X Z,Shum K P,Guo Y Q.L-Subvarieties of the variety of idem potent sem irings[J].A lgebra Universalis, 2001,46:75-96.

[3]Pastijn F,Zhao X Z.G reen’s D-relation for multip licative sem iring varieties[J].A rch.M ath.(Brno),2000, 36:77-93.

[4]张娟娟,李映辉,朱敏慧.两类幂等元半环[J].西北大学学报:自然科学版,2008,38(1):5-8.

[5]How ie JM.Fundam entals of Sem igroup Theory[M].Oxford:Oxford Science Publication,1995.

[6]G ratzer G.Universal A lgebra[M].New York:Springer-Verlag,1979.

[7]张娟娟,冯锋.幂等元半环簇P[J].纯粹数学与应用数学,2005,21(1):68-72.

Two kinds of idempotent semirings with identity element

LIUWei,HU Jing,FENG Pi-hu

(Department of Mathematics,Northwest University,Xi’an 710127,China)

To study the properties of them embers of two im potent subvarieties of the variety of idem potent sem irings with identity elem ent.The equivalent of them are characterized and the structure of them are discussed.Some resu lts about themembers of two im potent subvarieties are obtained.

idem potent sem iring,m onobisem ilattice,M al’cev product,variety

O152.7

A

1008-5513(2009)02-0289-05

2008-05-21.

国家自然科学基金(10471112),陕西省教育厅自然科学专项基金(07JK 413).

刘伟(1982-),硕士,研究方向:半群代数理论.

2000M SC:08A 15