矩阵特征多项式的图论计算公式

2009-07-05谭尚旺

纯粹数学与应用数学 2009年2期

关键词：图论邻接矩阵有向图

谭尚旺

(中国石油大学应用数学系,山东东营 257061)

矩阵特征多项式的图论计算公式

谭尚旺

(中国石油大学应用数学系,山东东营 257061)

给出了赋权有向图邻接矩阵特征多项式的图论计算公式,从而得到了一般矩阵特征多项式的图论计算方法,并且研究了赋权有向图邻接矩阵特征多项式和谱半径的一些性质.

矩阵;赋权有向图;线性子图;特征多项式

1 引言

文中没有定义的概念和记号见文[1].令A=(aij)是数域F上的n阶矩阵,则它的伴随有向图定义为赋权有向图DA=(V,E),V={v1,v2,…,vn},其中当且仅当aij/=0时,vi到vj有一条权值为aij的有向边.显然,A是赋权有向图DA的邻接矩阵.因此,一般矩阵特征多项式的计算问题与一般赋权有向图邻接矩阵特征多项式的计算问题是等价的.

设D是顶点集为V(D)且边集为E(D)的赋权有向图,wD(e)表示有向边e在D中的权. 设H是D的一个子图,如果对每个边e∈E(H),都有wH(e)=wD(e),则称H是D的一个赋权有向子图.令H是D的赋权有向子图.如果V(D)/=V(H)或E(D)/=E(H),则称H是D的赋权有向真子图.如果V(D)=V(H),则称H是D的生成赋权有向子图.D的一个i阶赋权有向子图H称为D的一个i阶线性子图,如果H的每个点的入度和出度都是1.显然,D的一个线性子图是由一些顶点不交有向圈的并构成的,其中这里把环看成长度为1的有向圈.对于D的赋权有向子图H,如果E(H)/=∅,则定义它的权wD(H)为wD(H)=∏e∈E(H)wD(e).

图谱研究是图论的热点之一,如文[2]研究了具有特殊谱的图的结构,文[3]研究了特殊图的谱特征.如何快速计算矩阵的特征多项式对研究和计算矩阵的谱是重要的.另一方面,网络和电路设计中的图一般都是赋权有向图并且赋权有向图的谱时常用来解决具体问题.因此,研究矩阵或赋权有向图邻接矩阵特征多项式的计算问题是有意义的.1974年,文[4]给出了一般无向图邻接矩阵特征多项式的图论计算公式.2000年,文[5]给出了一般有向图邻接矩阵特征多项式的计算公式.本文首先研究了一般矩阵或赋权有向图邻接矩阵特征多项式的图论计算方法,然后研究了非负矩阵或赋权有向图特征多项式和谱半径的一些性质.

2 赋权有向图特征多项式的图论计算方法

本节研究赋权有向图特征多项式的图论计算方法.记n阶赋权有向图D的邻接矩阵A(D)的特征多项式为φ(D,λ)或φ(D),令

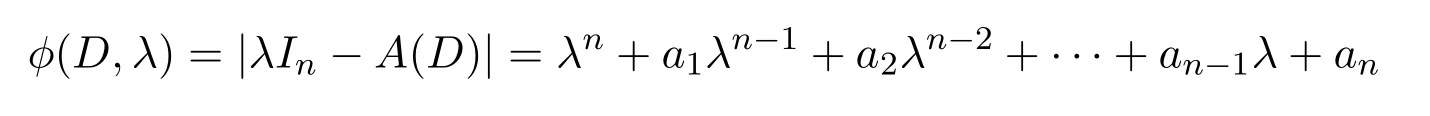
对D的赋权有向子图H,约定H−V(H)=∅时,φ(H−V(H),λ)=1.

引理2.1[6]令Li是D的i阶线性子图的全体,ε(H)是H中的圈数,则

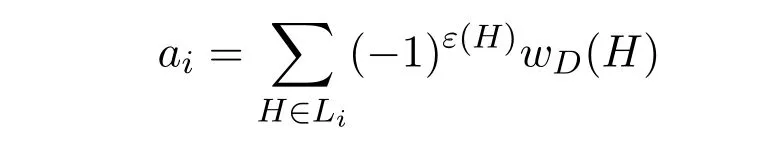
其中当Li=∅时,约定和号取值为0.

定理2.1设v是n阶赋权有向图D=(V,E)的一个顶点,C(D,v)表示D中包含顶点v的所有有向圈的集合,则

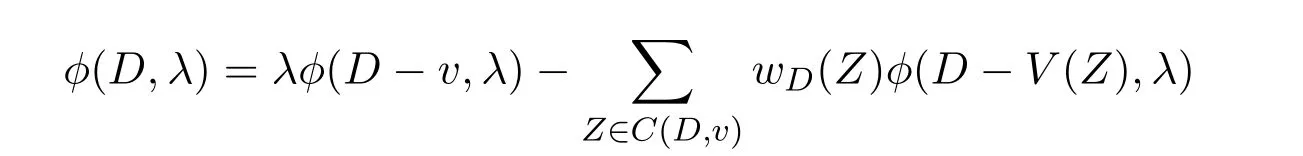
证明记D的一个赋权有向子图H的阶为o(H).引进记号

对i=0,1,…,n,下面只要证明φ(D,λ)与g(λ)−h(λ)的λn−i的系数相等即可.显然,λn的系数相等且都为1.因此,下面假设i≥1.取定D的一个i阶线性子图Hi,以Hif(λ)表示Hi对多项式f(λ)的λn−i系数的贡献.对常数a,特别约定Hi(af(λ))=aHif(λ).则对任意的常数a,b和多项式p(λ),q(λ),都有

由引理2.1知Hiφ(D,λ)=(−1)ε(Hi)wD(Hi).下面分两种情形讨论Hi对g(λ)−h(λ)的λn−i系数的贡献.

情形1假设v/∈V(Hi).

显然,g(λ)的λn−i系数取决于φ(D−v,λ)的λn−i−1系数.由于o(D−v)=n−1,于是对φ(D−v,λ)的λn−i−1系数有贡献的D−v的线性子图的阶是i.因为v/∈V(Hi),所以Hi也是D−v的一个i阶线性子图.于是由引理2.1知

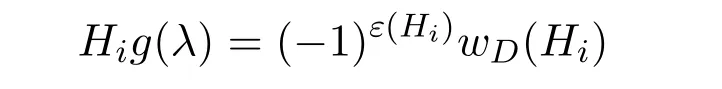
任取Z∈C(D,v).由于o(D−V(Z))=n−o(Z),于是对φ(D−V(Z),λ)的λn−i系数有贡献的D−V(Z)的线性子图的阶为i−o(Z).既然Z不是Hi的分支,于是o(Hi−V(Z))≥i−o(Z)+1,从而Hi−V(Z)不是D−V(Z)的i−o(Z)阶线性子图,进而Hi−V(Z) 对φ(D−V(Z),λ)的λn−i系数贡献为0,即Hi(φ(D−V(Z),λ))=0.因此,有

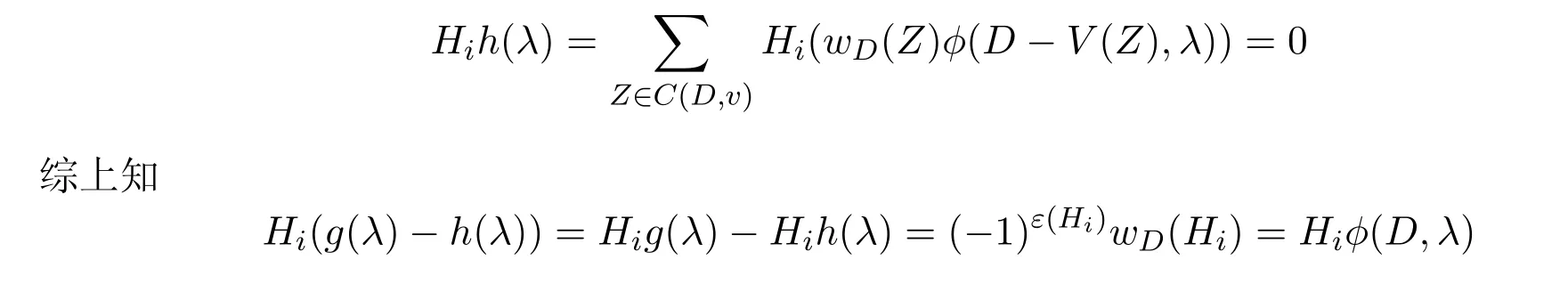
情形2假设v∈V(Hi).

显然,o(Hi−v)=i−1并且o(D−v)=n−1.因此,Hi−v不是D−v的i阶线性子图,从而Hi−v对φ(D−v,λ)的λn−i−1的系数贡献为0,即Hig(λ)=0.

由线性子图的定义,C(D,v)中只有一个圈在Hi中,记该圈为K,则Hi−V(K)是D−V(K)的i−o(K)阶线性子图.既然o(D−V(K))=n−o(K),于是Hi−V(Z)对φ(D−V(K),λ) 的λn−i系数贡献为

对每个Z∈C(D,v){K},Z都不是Hi的分支,所以o(Hi−V(Z))≥i−o(Z)+1,从而Hi不是D−V(Z)的i−o(Z)阶线性子图,于是Hiφ(D−V(Z),λ)=0.因此,有

根据上面两种情形的讨论,我们完成了定理的证明.

推论2.1设u和v分别是无公共顶点赋权有向图D1和D2的顶点,D表示把u和v粘成一个顶点后得到的赋权有向图,则

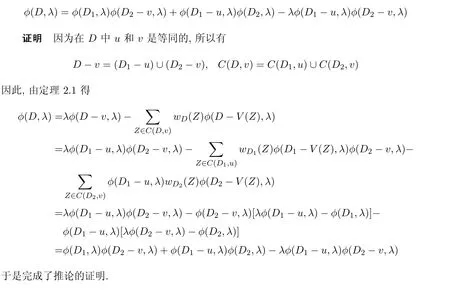
对i=0,1,2,…,n,下面只需证明φ(D,λ)和φ(D−e,λ)−h(λ)的λn−i的系数相等即可.显然,λn的系数相等且都为1.因此,下面假设i≥1.取定D的一个i阶线性子图Hi,下面需要证明Hi对φ(D,λ)和φ(D−e,λ)−h(λ)的λn−i的系数贡献相同.仍然沿用定理2.1中的记号,由引理2.1知Hiφ(D,λ)=(−1)ε(Hi)wD(Hi).下面分两种情形讨论Hi对φ(D−e,λ)−h(λ) 的λn−i系数的贡献.

情形1假设e/∈E(Hi).

显然,Hi−e=Hi是n阶赋权有向图D−e的i阶线性子图.由引理2.1有

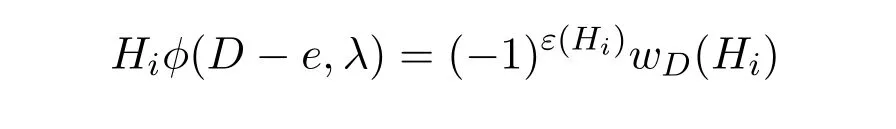
任取Z∈C(D,e).由于o(D−V(Z))=n−o(Z),于是对φ(D−V(Z),λ)的λn−i系数有贡献的D−V(Z)的线性子图的阶为i−o(Z).既然e/∈E(Hi),于是Z不是Hi的分支,从而o(Hi−V(Z))≥i−o(Z)+1.这表明Hi−V(Z)不是D−V(Z)的i−o(Z)阶线性子图.因此,Hi−V(Z)对φ(D−V(Z),λ)的λn−i系数贡献为0,即Hi(φ(D−V(Z),λ))=0.于是有

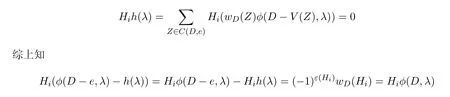
情形2假设e∈E(Hi).

显然,Hi−e是n阶有向图D−e的i阶有向子图,但不是D−e的i阶线性子图.因此, Hiφ(D−e,λ)=0.由线性子图的定义,C(D,e)中只有一个圈在Hi中,记该圈为K.类似定理2.1情形2的证明得

根据上面两种情形的讨论,我们完成了定理的证明.

推论2.3设vu是简单无向赋权图G=(V,E)的一个边,C(G,vu)表示G中包含vu的所有圈的集合,则

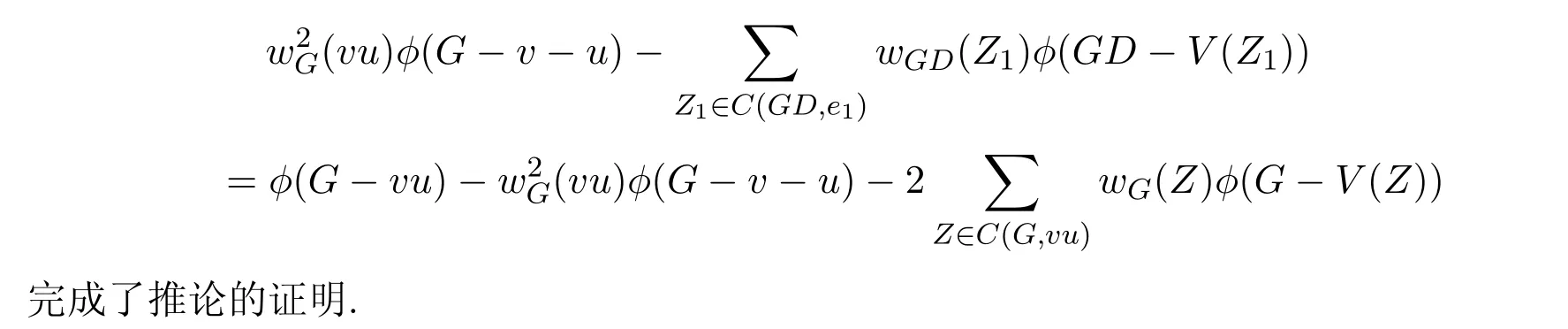
利用上面的结论,能够简单直观的计算许多矩阵的特征多项式.注意到简单无向图可以看成是边上的权值为1的赋权图,于是由推论2.2和推论2.3,能立即得到计算简单无向图邻接矩阵特征多项式的常用公式[4].

3 赋权有向图特征多项式的一些性质

本节研究赋权有向图特征多项式的性质.权值都是正数的赋权有向图称为正赋权有向图.由非负矩阵理论知正赋权有向图的邻接矩阵的谱半径是一个最大特征值.记赋权有向图D的邻接矩阵的谱半径为ρ(D).

引理3.1[4]设H和D都是正赋权有向图且D强连通,如果A(D)≥A(H)且A(D)/= A(H),或H是G的一个赋权有向真子图,则ρ(H)＜ρ(D).

引理3.2设e是正赋权强连通有向图D的一个边,则当λ≥ρ(D)时,都有φ(D,λ)＜φ(D−e,λ).

证明因为D是强连通的,所以C(D,e)/=∅.任取Z∈C(D,e).一方面,wD(Z)＞0.另一方面,由引理3.1知ρ(D)＞ρ(D−V(Z)),这表明λ≥ρ(D)时,φ(D−V(Z),λ)＞0.因此, 当λ≥ρ(D)时,由定理2.2得

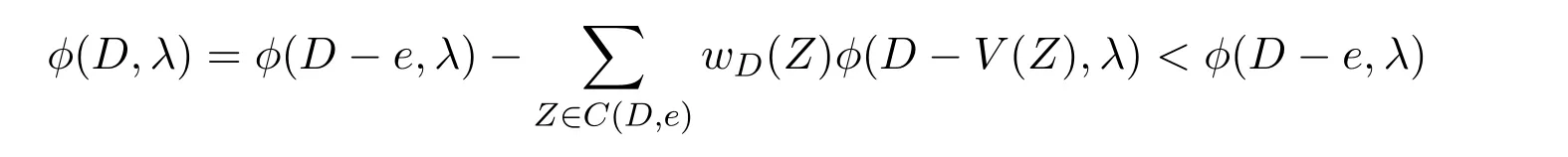
于是完成了引理的证明.

定理3.1如果H是正赋权强连通有向图D的一个真生成赋权有向子图,则当λ≥ρ(D) 时,有φ(D,λ)＜φ(H,λ).

[1]邦迪J A,默蒂U SR.图论及其应用[M].吴望名,李念祖,译.北京:科学出版社,1984.

[3]亓健,谭尚旺,同小军.完全等部二分图kn,n的迭线图Lm(kn,n)的谱特征[J].纯粹数学与应用数学,2000, 16(2):74-78.

[4]Cvetkovi´c D M,Doob M,Sachs H.Spectra of G raphs[M].New York:Academ ic Press,1980.

[5]谭尚旺,亓健,郭纪明.有向图和弱正则有向图补图的特征多项式的计算方法[J].数学杂志,2000,20(4):421-426.

[6]陈惠开.应用图论[M].范定松,张玲玲,译.北京:人民邮电出版社,1988.

(Department of App lied Mathematics,China University of Petroleum,Dongying 257061,China)

We obtain formulas computing the characteristic polynomial of ad jacent matrix of a weighted digraph in graph theory,thereby the methods computing the characteristic polynomial of a matrix in graph theory are derived and some properties of characteristic polynomial and spectral radius of adjacentmatrix on a weighted digraph are investigated.

matrix,weighted digraph,linear subgraph,characteristic polynomial 2000M SC:05C50