一种基于Tchebichef矩的半脆弱图像数字水印算法*
2009-05-08吕皖丽郭玉堂
吕皖丽,郭玉堂,2,罗 斌
(1. 安徽大学计算智能与信号处理教育部重点实验室//计算机科学与技术学院,安徽 合肥 230039;2. 安徽省教育学院计算机科学与技术系,安徽 合肥 230061)
数字水印技术是信息隐藏和数字产品版权保护及认证的有效技术,是多媒体信息安全研究领域的热点课题。在使用数字水印的方法对图像内容进行认证时,需要用到半脆弱数字水印技术。数字水印算法在实现上大体可分为空域中实现数字水印和变换域中实现数字水印两类。空域数字水印算法[1-2]的优点是简单易行、有较大的信息隐藏量,但该算法鲁棒性不好,属于脆弱数字水印技术,实用性差。在变换域中实现的数字水印算法中最典型的是Cox等人提出的DCT(discrete cosine transform)水印算法[3],将扩频通信的理论应用到了数字水印系统中。由于小波变换具有良好的主频分解特性,近年来还出现了许多基于小波变换的水印算法[4]。变换域水印属于鲁棒数字水印技术,对一般图像处理操作不敏感,但是算法复杂,水印容量低。为了增加变换域上水印容量,出现了利用数学分析或机器学习的方法来最优化水印嵌入位置、容量、强度的算法,如Lou等使用神经网络[5-6],但是,神经网络易产生过学习现象,且隐层节点数需要根据经验来确定。支持向量机是一种基于统计学习理论的新的通用学习方法,基于支持向量机的数字水印算法在较好保持图像感知质量的前提下,对部分图像处理具有很好的鲁棒性[7],但是由于支持向量机需要训练和学习,具有较高的时间和空间复杂度,嵌入水印容量相对较小而且对JPEG压缩敏感,因而还是欠缺实用性。近年来,图像的矩在图像分析和重建中得到了应用,在损失部分矩的情况下,图像重建时仍然可以得到质量较好的图像,利用这一特性,可以使用图像的矩进行数字水印的嵌入[8-9]。
文献[10]在Zernike矩中嵌入数字水印。常用的Zernike、Pseudo-Zernike以及Legendre 矩使用连续正交多项式作为基函数。实际应用中使用连续正交矩对数字图像进行处理时,采用离散求和的方式来逼近真实积分运算,连续函数离散化时会产生离散误差,并且多项式域到图像坐标域的转换造成实际矩计算中还存在着计算误差,这两大误差造成无法得到连续正交矩的准确值。离散正交矩的出现解决了误差难题。首先,离散误差不复存在了,而这一误差在计算连续正交矩中不可避免;其次,使用离散正交矩表示的图像更适宜用矩阵运算[11]。
基函数采用Tchebichef多项式的Tchebichef离散正交矩非常适用于数字图像处理。首先,Tchebichef正交矩本身是离散的,计算精度较高;其次,Tchebichef矩可直接用于离散图像,不需要对定义域进行归一处理;最后,Tchebichef多项式的计算具有递推关系和对称性。这些优点使得Tchebichef正交矩在图像重建时可以得到非常精美的图像,因此不仅适合用来提取图像特征,也很适宜在数字水印算法中用来嵌入水印。
1 Tchebichef矩
1.1 连续正交矩和离散正交矩
对于连续函数f(x,y),可以得到连续正交矩

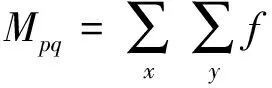
这一离散化的过程将导致连续矩函数的离散误差。
1.2 Tchebichef 矩
离散Tchebichef多项式定义如下[10]:
tn(x) = (1-N)n 3F2(-n,-x,1 +n;1,1-N;
1)n,x,y=0,1,2,...,N-1
(1)
其中

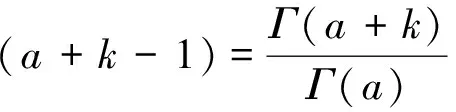
离散Tchebichef多项式满足正交属性:

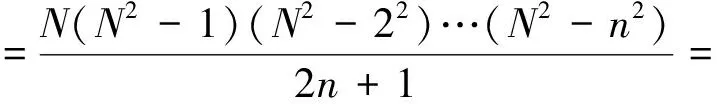

(2)
函数f(x,y),0≤x,y≤N-1,满足
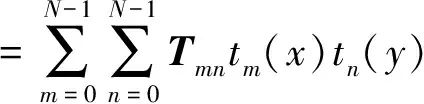
(3)
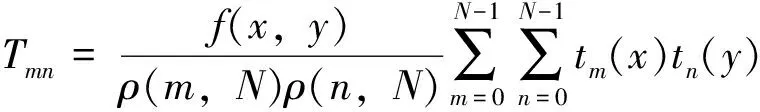
(4)
归一化的Tchebichef多项式定义为:
(5)
其中β(n,N)是一个与x无关的常量,β(n,N)最简单的选择是β(n,N)=Nn,这样第n阶 Tchebichef多项式表示为:
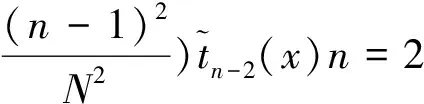
(6)
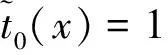

n=0,1,2,...,N-1。
2 数字水印的嵌入
数字水印的嵌入过程如图1。
2.1 基于Tchebichef矩的数字水印嵌入
数字水印的嵌入过程如下:
第1步 将水印图像转换成为一维序列,使用版权拥有者的密钥K对水印进行加密置乱,得到W={ωi}|i = 1…m,其中m是数字水印的长度。

图1 数字水印的嵌入过程

(7)


第3步 对第i个块,计算T45和T54,如果嵌入的第i位数字水印ωi是0,调整T45和T54,使T45
第4步 使用系数矩阵Ti重建图像I的第i个块Ii:
(8)
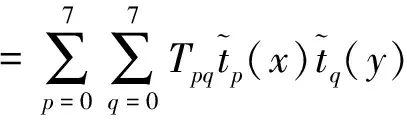
2.2 计算Tchebichef矩的快速算法



图2 N=8时归一化的Tchebichef多项式
3 数字水印的提取过程
本文中数字水印的提取不需要原始图像参与,属于盲水印提取算法。水印的提取过程是水印嵌入过程的逆过程,如图3所示。

图3 数字水印的提取过程
数字水印提取过程步骤如下:
第1步 将嵌入水印的图像I′分成8×8像素的块,对每一块计算Tchebichef矩,系数排列成8×8的矩阵。

第3步 使用版权拥有者的密钥K对水印进行解密并逆置乱,得到提取的水印图像。提取出的水印的质量可以使用误码率BER来衡量。
4 仿真实验
4.1 决定水印嵌入矩位置及阈值

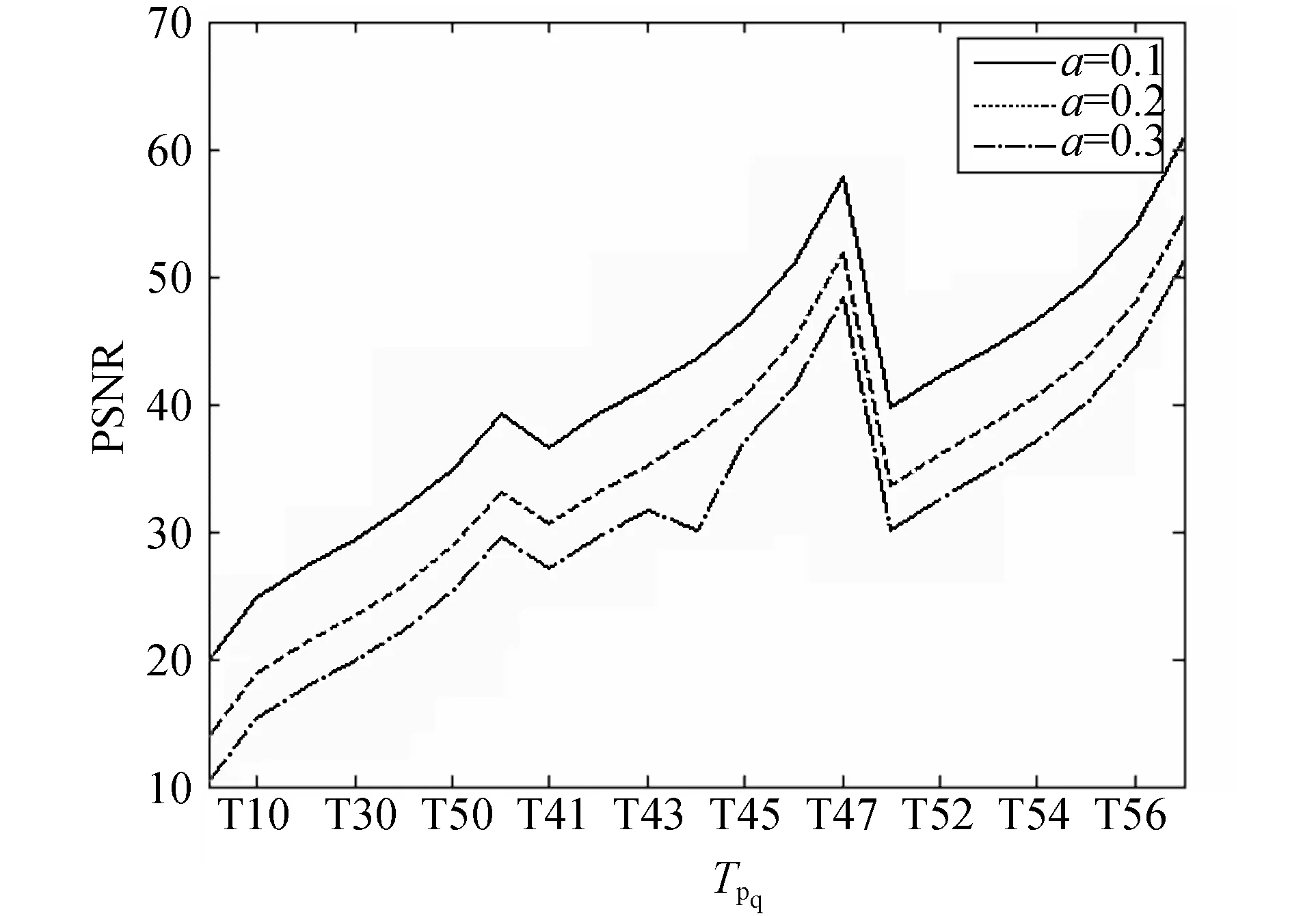
图4 修改块中一个Tchebichef 矩的块PSNR
结合图2的结果,为了使嵌入水印后的图像能够经受低通滤波,我们选择T45和T54来嵌入水印信息。
图5是标准图库中的五幅待测试的原图和水印图像,五幅原图分别代表具有纹理丰富、细节丰富、区域分明、主题分明和平坦背景的五类图像。
图6是在原始图像中使用不同阈值τ嵌入不同水印位数的嵌入水印图像的PSNR,从图6中可以看出,随着阈值τ的增加及嵌入水印数量的增加,嵌入水印图像的PSNR会下降。

图5 原始图像和水印图像
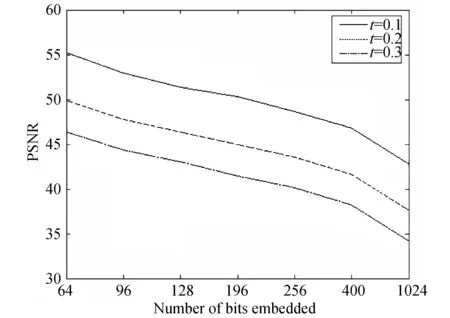
图6 使用不同阈值τ嵌入不同水印位数的嵌入水印图像的PSNR
表1是在原始图像中使用不同阈值τ嵌入不同水印位数的嵌入水印图像中提取水印的误码率。从表1中可以看出,阈值τ增大,提取水印的误码率降低。当τ从0.2增加到0.3时,误码率相差已不多,但是PSNR差别仍然较大。
综合图4、图6和表1的结果,选用阈值τ为0.2。后面的实验中,在256×256的原始图像中嵌入32×32的水印图像。实验结果与传统使用DCT变换嵌入水印算法做比较[12]。文献[12]将原始图像分块后做DCT变换,修改中频系数来嵌入数字水印。为了使实验具有可比性,本文使用的DCT水印算法同样将原始图像分为8×8的块,将每块做DCT变换,修改两个中频系数嵌入水印。
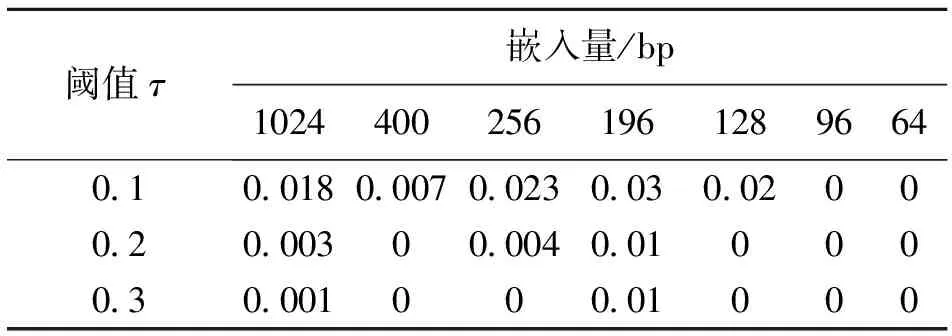
表1 使用不同阈值τ嵌入不同水印位数的嵌入水印图像中提取水印的误码率BER
以Pepper为例,图7中从左到右分别为Pepper原图,使用本文方法添加水印Pepper图和传统使用DCT添加水印Pepper图。

图7 Pepper原始图像和添加水印后图像
4.2 抗JPEG压缩的鲁棒性实验
使用Stirmark对添加水印图像进行压缩质量从90到10的JPEG压缩,对压缩后的图像提取水印,表2给出实验结果并与传统使用DCT变换嵌入水印算法做比较[12]。

表2 抗JPEG压缩鲁棒性实验
经过不同压缩质量的JPEG压缩,使用本文算法提取的水印普遍比使用DCT变换提取的水印效果好。
4.3 抗加性噪声的鲁棒性实验
图像的噪声可以看做是图像的高频信息,表3给出了实验过程中对高斯、椒盐噪声进行的鲁棒性实验结果并与传统使用的DCT变换嵌入水印算法做比较。从表3中可以看出,使用本文算法进行数字水印嵌入,抗加性噪声能力明显比使用DCT方法强。
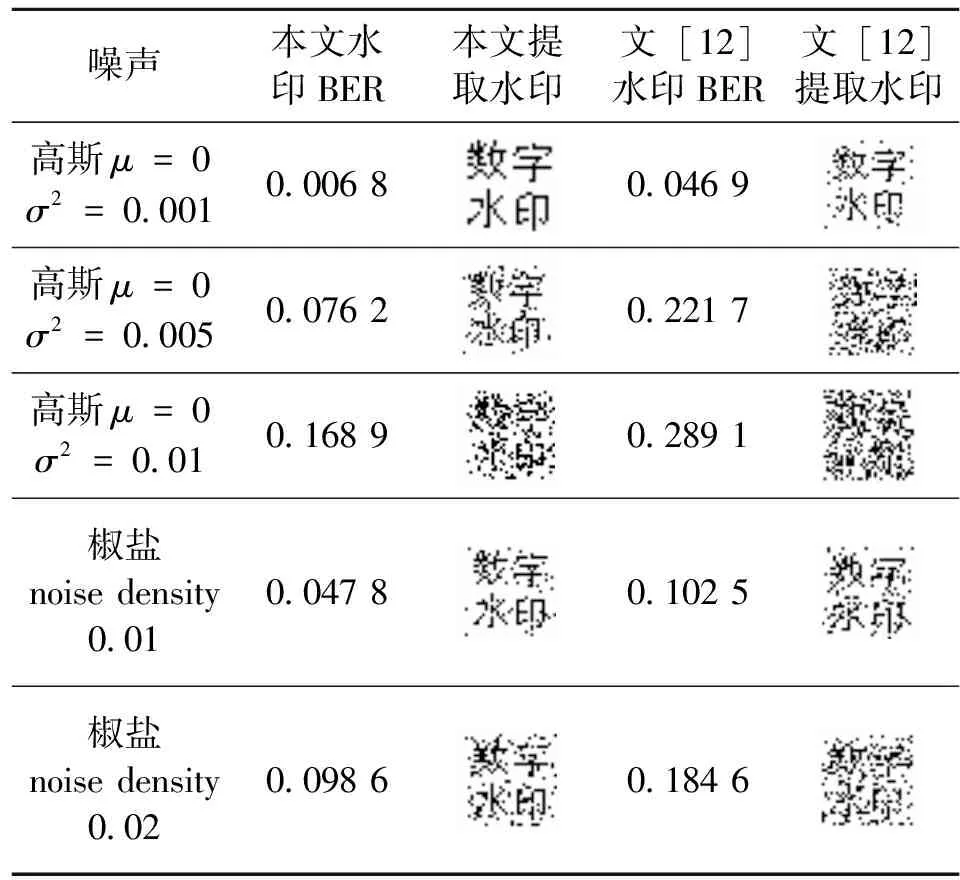
表3 抗高斯椒盐噪声鲁棒性实验
4.4 抗仿射攻击的鲁棒性实验
使用Stirmark对添加水印图像旋转并缩放回原始图像大小,对攻击后的图像提取水印。表4给出了实验结果。经过顺时针和逆时针的小角度旋转,原始水印仍然清晰可辨。
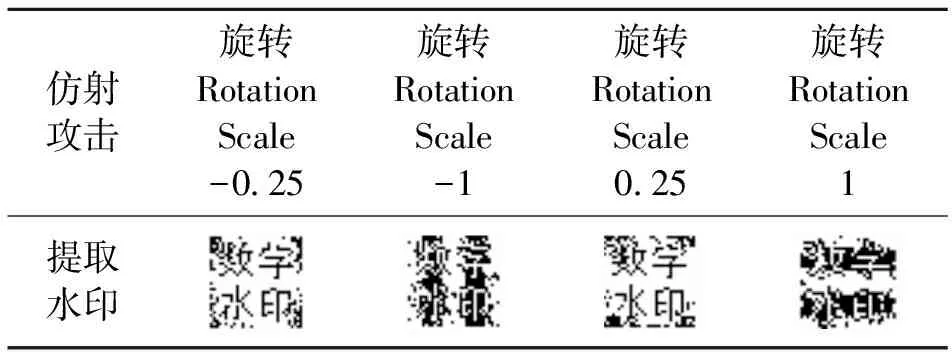
表4 仿射攻击鲁棒性实验
4.5 抗亮度/对比度攻击的鲁棒性实验
图8给出了使用Photoshop对添加水印图像增加亮度/对比度后水印检测实验结果。当亮度增加70,对比度也增加70后,误码率仅为0.005 9;而使用传统基于DCT变换的数字水印算法,提取水印误码率为0.018 6。
4.6 抗高斯低通滤波的鲁棒性实验
对加载水印图像进行高斯低通滤波,分别设计窗口为3×3、5×5和7×7的高斯低通滤波器,基于Tchebichef矩的数字水印算法取得了非常好的实验效果,实验结果如图9所示。

图8 抗亮度/对比度攻击的鲁棒性
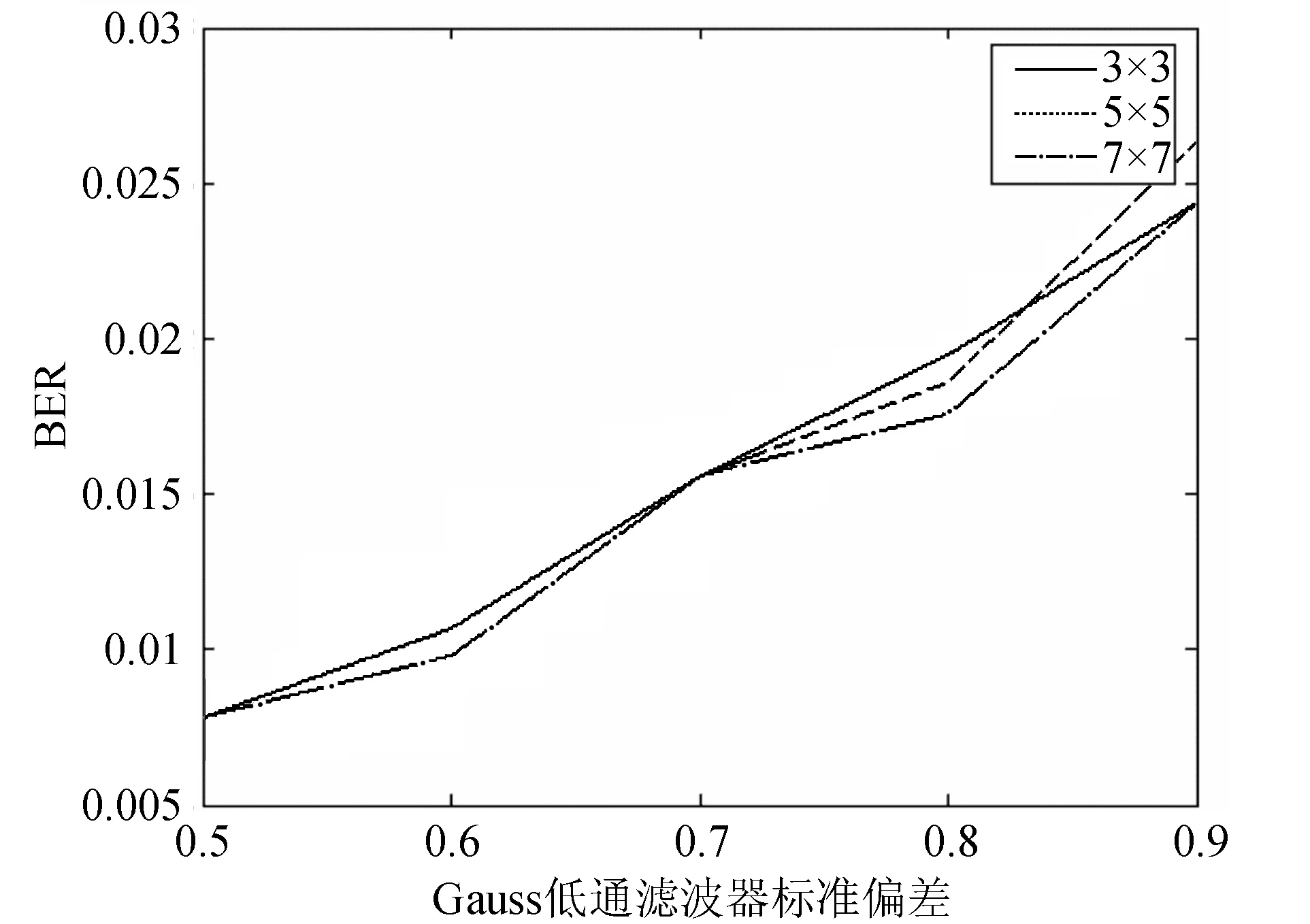
图9 抗低通滤波的鲁棒性
4.7 对剪切攻击的实验
使用Photoshop对添加水印图像进行了部分剪切和拷贝,选择不具备抗剪切功能的图像置乱算法,检测出的水印可以记忆被剪切和拷贝部位。
如果选取合适的特征提取算法和水印置乱算法,本文算法不仅可以定位拷贝篡改部位,还可以定位从图像的何处拷贝而来,因而可以应用于图像内容认证算法。
5 结 语
本文通过修改图像的Tchebichef矩来实现数字水印的嵌入,算法通过查找表法实现水印算法的快速计算,大大降低了计算Tchebichef矩的时间复杂度,提高了实现速度,使水印的添加和检测具有实时性。实验表明:算法不仅视觉效果好,而且对于常见的攻击,如JPEG压缩、加性噪声、小角度的旋转缩放攻击、亮度/对比度攻击以及高斯低通滤波等具有很好的鲁棒性,实验效果远好于常用的DCT数字水印算法。基于Tchebichef矩的半脆弱数字水印算法在实际应用中具有很强的实用价值。本文基于Tchebichef矩的半脆弱数字水印算法在水印嵌入容量上仅仅考虑最多嵌入1024bit,实际应用中,可以根据视觉模型,在纹理较丰富的块中修改多个Tchebichef矩来增加水印容量,采用什么有效快速的算法来判断水印嵌入位数,这也是我们下一步需要做的工作。
参考文献:
[1] VAN SCHYNDEL R G, TIRKEL A Z, OSBOME C F. A digital watermark[C]. Proceedings of the IEEE International Conference on Image Processing, Austin, Texas, USA. 1994: 86-90.
[2] NIKOLAIDIS N, PITAS I. Copyright protection of images using robust digital signatures[C]. Proceedings of theIEEE International Conference on Acoustics,Speech,and Signal Processing,Atlanta,Georagia,USA. 1996: 2168-2171.
[3] COX I J, KILIAN J, LEIGHTON F T, et al. Secure spread spectrum watermarking for multimedia[J]. IEEE Transactions on Image Processing, 1997, 12(6): 1673-1687.
[4] HSU C T, WU J L. Multiresolution watermarking for digital image[J]. IEEE Transactions on Circuits and System-II: Analog and Digital Signal Processing, 1998, 45(8) : 1097-1101.
[5] LOU D C, LIU J L, HU M C. Adaptive digital watermarking using network technique[C]. Proceeding of the IEEE International Carnahan Conference on Security Technology, Taipei, 2003: 325-332.
[6] DAVIS K J, NAJARIAN K. Maximizing strength of digital watermarks using neural networks[C] . Proceedings of the International Joint Conference on Neural Networks, Washington DC, USA, 2001: 2893-2898.
[7] HUNG H T, DUEN W S. Color image extraction based on support vector machines[J]. Information Sciences, 2007,177: 550-569.
[8] ZHANG L, XIAO W W, QIAN G B, et al. Rotation, scaling, and translation invariant local watermarking technique with krawtchouk moments[J]. Chinese Optics Letters, 2007, 5 (1):21-24.
[9] HU M. Visual pattern recognigion by moment invariants[J]. IRE Trans Inf Theory, 1962, 8 : 179-187.
[10] XIN Y Q, LIAO S, MIROSLAW P, Circularly orthogonal moments for geometrically robust image watermarking[J]. Pattern Recognition, 2007,40:3740-3752.
[11] MUKUNDAN R. Image analysis by Tchebichef moments[J]. IEEE Transactions on Image Processing, 2001,(9):1357-1364.
[12] BARNI M, BARTO LINI F, CAPPELLINI V. A DCT domain system for robust image watermarking[J]. Signal Processing, 1998, 66(3): 357-372.
