从数轴上理解绝对值

刘卫华

我们知道:|x|的几何意义是数x在数轴上的对应点到原点的距离.|x-a|的几何意义是数x和数a在数轴上的对应点之间的距离.因此,绝对值的几何意义总可以通过数轴来体现,让绝对值和数轴结合,是解决一些问题的巧妙方法.

例1已知|x|=1,则x=______.

分析:有的同学习惯上写成x=1,其实,我们结合数轴,可以看出,到原点距离为1的点,有两个.

解:x=1或-1.

例2绝对值大于3而小于6的所有的整数为________.

分析:有的同学习惯上写成4､5,我们结合数轴来看,到原点的距离大于3而小于6的点,在原点两边都有,且它们关于原点对称.

解:4或-4,5或-5.

例3若|x+1|+|x-3|=4,则整数x的可能值是________.

分析:这是一个方程,我们目前不好处理,我们运用绝对值的定义来试一试.

解:由绝对值的定义得x+1的绝对值是表示x与-1点之间的距离,x-3的绝对值是表示与+3点之间的距离.作数轴,如图1,在数轴上,我们看到-1和3之间的距离正好是4,所以若x在-1的左边,则x与-1点之间的距离加上x与3点之间的距离的和必大于4(如图2),不符合题意;

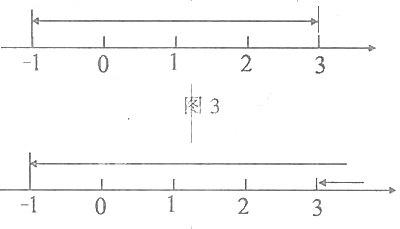
若x在-1和3之间(包括-1和3),则x与-1点之间的距离加上x与3点之间的距离的和等于4(如图3),符合题意,从中找出-1､0､1､2､3这几个整数点;

若x在3的右边,则x与-1点之间的距离加上x与3点之间的距离的和大于4(如图4),不符合题意.

综上所述,整数x的可能值是-1､0､1､2､3.

由以上例题我们可以看出,结合数轴去分析,才能更全面解答问题.数轴,是我们学习中的一个重要的工具,借用它,我们能更好理解绝对值的含义.大家一定要牢记!