高中新课程“数学史选讲”应讲些什么
2008-07-31国佳
国 佳
《普通高中课程标准》基本理念之一就是在高中数学课程中体现数学的文化价值,明确规定数学史选讲被纳入高中数学课程,但这部分内容“教什么”普遍是令高中教师比较头疼的问题.
平面解析几何是17世纪最重要的数学成就之一,在数学史上具有划时代意义,具有丰富的文化价值和教育价值,是提高学生科学素养和整体文化认知水平的典型范例.另外在每年的高考数学试卷中都占有重要位置,是高考复习的重点和难点.但绝大多数教师的传统观念认为学生学习解析几何主要就是学会代数计算和方法,很少介绍解析几何产生的背景,没有真正理解解析几何蕴含的思想方法.虽然数学史内容已包含在新课程的选修系列3中,但经调查实施状况并不理想,许多高中教师对这部分内容也感到陌生.
本文以平面解析几何的产生为专题,重点介绍笛卡儿和费马的解析几何思想,希望能有助于高中数学史课程的实施,并为高中教师对这部分内容的讲授提供参考.
1 平面解析几何的基本思想及重要前驱
在解析几何学创立之前,数学研究的对象是数与形,代数与几何这两个古老的数学分支各自独立地存在与发展,解析几何的诞生,使代数与几何实现了有机的统一.解析几何的基本思想是在平面上引进所谓“坐标”的概念,并借助这种坐标在平面上的点和有序实数对(x,y)之间建立一一对应的关系.每一对实数(x,y)都对应于平面上的一个点;反之,每一个点都对应于它的坐标(x,y).以这种方式可以将一个代数方程f(x,y)=0与平面上一条曲线对应起来,于是几何问题归结为代数问题,并反过来通过代数问题的研究发现新的几何结果.
早在公元前2000年,美索不达米亚地区的巴比伦人已能用数字表示一点到另一固定点的距离,已有原始的坐标思想.
公元前4世纪中叶古希腊数学家阿波罗尼奥斯全面论述圆锥曲线性质时采用过一种“坐标”,以圆锥体底面的直径作为横坐标,过顶点的垂线作为纵坐标.
14世纪法国数学家奥雷姆是解析几何最重要的前驱,他在《论形态幅度》这部著作中借用“经度”、“纬度”这两个地理学术语来描述他的图线,相当于横坐标与纵坐标.他的思想已接触到在直角坐标系中用曲线表示函数的图像,他的中心思想是用图形来表示一个变量的值,这个量依赖于另一个量,这可以说是函数概念及函数图像法的萌芽.
16世纪末,韦达提出了用代数方法解决几何问题的想法,给解析几何的创立很大启发.
17世纪初,开普勒发现行星围绕太阳运动的轨迹是椭圆,提出了行星运动三大定律,伽利略提出各种抛射体的运动轨迹是抛物线,这些都要求数学从运动变化的观点研究问题,并引起人们对圆锥曲线的兴趣,从客观上促进了解析几何的建立.
解析几何的真正发明还要归功于法国另外两位数学家笛卡儿与费马,他们工作的出发点不同,但却殊途同归.
2 笛卡儿与平面解析几何
笛卡儿(1596-1650)是法国杰出的哲学家、物理学家和数学家,又是生物学的奠基人.在笛卡儿之前,几何和代数这两个学科早就发展起来了,笛卡儿认为,欧几里得几何过分强调证明的技巧性,过分依赖于图形,不利于提高人们的想象力;代数又完全受法则和公式的约束.他主张把逻辑、代数、几何三者的优点结合起来,建立一种“普遍的数学”.笛卡儿创立解析几何的要旨是把几何问题归结为代数形式的问题,用代数学方法进行计算、证明,从而达到最终解决几何问题的目的,即几何代数化的方法.
笛卡儿解析几何的基本思想包括:
(1)引入坐标观念:受到法国人奥雷姆思想的影响,从经纬度出发,指出平面上的点和实数对(x,y)的对应关系.
(2)利用坐标法,提出用曲线表示方程的思想:考虑二元方程f(x,y)=0的性质,满足这方程的x,y值无穷多.x,y不同的数值所确定的平面上许多不同点,便构成一条曲线.这样,一个方程就可以通过几何的直观和方法来处理.
(3)利用代数方法,提出了用方程表示曲线的思想:具有某种性质的点,它们之间的关系可用一个方程表示.
笛卡儿在1637年出版了《更好地推理和寻求科学真理的方法论》,《几何学》是其中三个附录之一,大约占100页,《几何学》被认为是解析几何创立的标志.他首先改善了符号代数记法,他用小写字母a,b,c等代表已知量,x,y,z等代表未知量,这种用法一直延续至今.他设计用数字上标代替“平方”“立方”等词语表达法,对于希腊人来说,一个变量相当于某线段的长度,两个变量的乘积相当于某个矩形的面积,三个变量的乘积相当于某长方体的体积,三个以上变量的乘积,希腊人就没法处理了.笛卡儿则把x2看作比例式1∶x=x∶x2的第四比例项.因为对于一个量而言,其平方和立方跟该量本身并无质的区别.笛卡儿以单位量和比例式1∶x=x∶x2=x2∶x3=L为例说明数字上标仅表示跟单位量联系所需的“关系”数目.x只通过一个“关系”(比)跟单位量联系在一起,x2则要通过两个“关系”与单位量联系在一起.据此可以用算术语言引进几何.
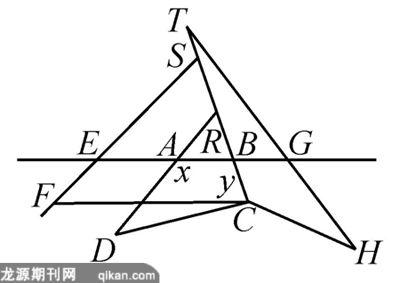
笛卡儿在《几何学》第二卷中,用“不确定的”代数方程研究几何曲线,证明了著名的希腊数学问题——帕波斯问题:设在平面上给定四条直线AG、GH、EF和AD,求从C点作四条直线CB、CD、CF和CH分别与已知直线交于已知角,且满足关系CB·CF=CD·CH的点的轨迹.他的解法中包含了解析几何主要思想:假定C点已找到,记AB为x,BC为y,经几何分析,他用已知量表出CD、CF和CH的值,代入CB·CF=CD·CH,就得到一个关于x和y的二次方程y2=Ay+Bxy+Cx+Dx2,其中A、B、C、D是由已知量组成的简单代数式.于是他指出,任给x一个值,就得到一个关于y的二次方程,从这个方程可以解出y.如果我们取无穷多个x值,就得到无穷多个y值,从而得到无穷多个点C,这些点C的轨迹就是二次方程代表的曲线.在这道题中笛卡儿选取直线AB作为基线(相当于一根坐标轴),以点A为原点,x值是基线的长度,y值是另一条线段的长度,该线段从基线出发,与基线交成定角.正是如此,笛卡儿建立了历史上第一个倾斜坐标系.由此,他把几何曲线变成代数方程,然后通过研究代数方程来揭示曲线的性质.他断言,方程的次数与坐标轴的选择无关,指出这个轴要选得使最后得出的方程愈简单愈好.
3 费马与平面解析几何
费马(1601-1665)是一名律师,虽然数学只是他的业余爱好,但他对数学做出了极为重要的贡献.费马与笛卡儿不同,他对于曲线的探讨,出发点是竭力恢复失传的阿波罗尼奥斯的著作《论平面轨迹》,费马撰写了《平面与立体轨迹引论》,他认为古人对于轨迹没有给予充分而又一般的表示,要解决这一问题,只能借助代数.
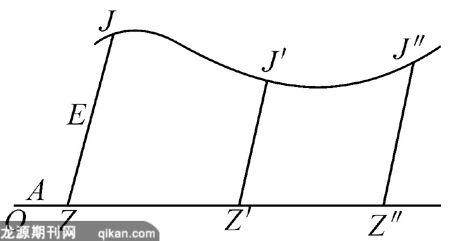
费马是这样考虑曲线和它上面的点(如右图),他取一条水平的直线作为轴,并在此直线上确定一个点作为原点,一般的点J的位置由A,E两个字母确定.A是从点O沿底线到点Z的距离,E是从点Z到J的距离,他所用的坐标是斜坐标,y轴没有明确标出,而且不用负数.这里的A和E相当于现在的x,y.费马的解析几何原理是:只要在最后的方程中出现两个未知量,我们就有一条轨迹,这两个量之一的末端描绘出一条直线或曲线.图中对于不同位置的J,其末端J,J′,J″,……就描绘出一条曲线来.这里的未知数A,E皆为变量.或者说联系A,E的方程是不定的.但他规定,如果方程是一次的,就代表一条直线;如果是二次的,就代表圆锥曲线.例如,他指出Dx=By(用我们现在的记号)代表一条直线;a2-x2=y2是圆的方程;a2-x2=ky2是椭圆方程;a2+x2=ky2是双曲线方程;x2=ay是抛物线方程.但有一点要注意,因为费马不用负坐标,他的方程不能代表整个曲线.
总之,费马主要是继承了希腊人的思想,他的成功之处在于把希腊数学中所发现的曲线特征,通过引进坐标译成了代数语言,这使得不同的曲线有了代数方程的一般表示方法.而笛卡儿从批判传统出发,费马从方程出发研究轨迹,而笛卡儿则从轨迹建立方程,方法各有侧重,但从历史的角度来看,笛卡儿的做法更具突破性.
参考文献
[1] 李文林. 数学史概论[M]. 北京:高等教育出版社,2002,8.
[2] 张贵新. 数学发展简史[M]. 东北师范大学出版社,1992,7.
[3] 梁宗臣,王青建,孙宏安. 世界数学通史[M]. 辽宁教育出版社.
[4] 吴文俊. 世界著名数学家传记[M]. 北京:科学出版社,1995,10.
[5] 朱家生. 数学史[M]. 北京:高等教育出版社,2004,7.
[6] 舒昌勇 高中数学新课程选修系列3、4的开课现状与思考[J]. 数学通报,2007,10:11-12.
[7] 李铁安,宋乃庆. 高中解析几何教学策略——数学史的视角[J]. 数学教育学报,2007,5:90-94.
[8] 张楠,罗增儒. 对数学史与数学教育的思考[J]. 数学教育学报,2006,8:72-75.
[9] 王宪昌. 关于数学文化研究的几点思考[J]. 数学教育学报,2007,2:44-47.
