美国与我国数学教材中关于“函数”概念教学之比较研究
2008-07-31俞昕
俞 昕
我国的高中数学教学改革正在如火如荼的进行着,从全球视野与国际交流的观点来看,我们的教学改革应放眼世界,需要在平等交流与相互沟通的基础上健康发展.笔者从教学前辈处得到一本现行美国的高中数学教材,笔者仔细翻阅了教材,发现与我国现行的高中数学新课程存在相同点,但更值得研究的是,它们之间又存在很多方面的差异,教材的布局、顺序、教学的方式方法等等,这些都引起了笔者很大的兴趣.“函数(Functions)”是我国高中数学中一个贯穿始终的重要概念,在美国的教材中它也扮演着重要的角色,所以笔者选择“函数”作为比较对象.
本文旨在就美国与我国教材中关于“函数”部分的教学情况进行比较研究,从中寻找异同点,为我们正在进行的高中数学教学改革提供一定的参考价值,同时以期待获得一些关于函数概念教学的值得我们借鉴的经验.
1 “函数”的教材处理与布局
我国的数学教材中是通过“在初中我们已经学习过函数的概念,并且知道可以用函数描述变量之间的依赖关系.现在我们将进一步学习函数及其构成要素.下面先看几个实例……”作为函数教学的引言;给出“函数”的集合形式定义,研究初中里学过的函数的定义域和值域;介绍区间的概念;最后通过两个例题来强化学生对函数的理解.
在美国的教材中,一开始就明确指出了Objectives(目标):(1)Determine Whether a Relation Represents a Function(判断给出的关系是否是函数关系);(2)Find the Value of a Function(求出函数值);(3)Find the Domain of a Function(求出函数的定义域);(4)Identifythe Graph of a Function(分辨函数的图象);(5)Obtain Information from or about the Graph of a Function(从函数的图象得到信息).然后给出提示:A relation is a correspondence between two sets. If x and y are two elements in these sets and if a relation exists between x and y, then we say that x corresponds to y or that y depends on x, and we write x→y. We may also write x→y as the ordered pair (x,y).(两个集合之间存在这样一种对应关系.如果x和y分别是这两个集合中的两个元素,并且在x和y之间存在着一种联系,那么我们可以说由x得到相应的y或者说y由x得到,我们可以记作x→y.我们也可以把x→y记作有序数对(x,y)). 接着教材就通过13个Examples来逐步阐述函数的概念和本质,并且逐一向学生展示应该如何达到教学与学习的目标.在这13个Examples中有些是通过叙述的形式,有些是通过问答的形式,从不同的角度来揭示“函数”这个重要的概念,并且占用了很大的篇幅.
笔者比较两个教材对“函数”概念教学的总体处理,发现以下几点区别:(1)美国教材中对“函数”概念的处理从篇幅上讲明显多于我国的教材.总共通过13个举例来逐层讲解函数概念,每个例子都有详细的解说过程,在几个例子后还有一些阶段性小结.我国的教材在给出函数概念后设计了两个例题,一个是求函数的定义域,求函数值;一个是判断两个函数是否是同一个函数.在中间穿插了三个“思考”,第一个思考是让学生总结函数有什么特征,第二个思考是研究反比例函数的定义域与值域,第三个思考是让学生比较研究初中和高中函数的两个定义.(2)我国的教材中在给出了函数的概念后穿插的给出“区间”的概念,而在美国的教材中,“区间”的概念在之前的章节中就已经介绍了,因此在讲解函数概念时就已经可以拿来使用了.这种处理方法笔者觉得还是比较可取的,因为“区间”的概念本身比较独立,可以提前至集合概念之后讲解,而在函数概念的讲解时就不必要腾出空间来介绍“区间”,可以对函数概念再进行深入的剖析.(3)在美国的教材中可以使用绘图计算器来研究函数图象.我国的教材中虽然在某些内容已经引进计算器的使用,但在函数图象的绘制上尚还没有引进绘图计算器,我们教师在平时的备课中经常会使用几何画板来绘制函数的图象,笔者觉得在必要的时候也可以向学生渗透计算机绘图的方法.
2 “函数”概念的引入
我国的教材中给出三个实例,让学生分析、归纳三个实例,发现它们的共同点.通过让学生思考、探究发现函数的特点,随后教材就给出函数的概念.美国的教材中对函数概念引入的处理与我国有些不同.Example 1 就是An Example of a Relation. 实例给出了四个学生与他们的生日之间的一种对应关系.

首先是通过上面这样的框图对应关系让学生感受函数是一种对应关系.Often, we are interested in specifying the type of relation (such as an equation) that exists between the two variables. For example, the relation between the revenue R resulting from the sale of x items selling for $10 each may be expressed by the equation R=10x. If we know how many items have been sold, then we can calculate the revenue by using the equation R=10x. This equation is an example of a function.在给出一些实例后教材给出the definition of a function: Let X and Y be two nonempty sets A function from X into Y is a relation that associates with each element of X exactly one element of Y.
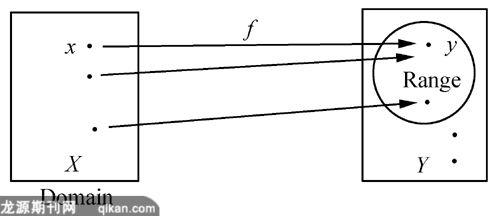
从两个教材对“函数”概念引入的处理上分析,我国的教材着重让学生自己进行分析,得出函数的特点,而美国的教材则更注重对实例进行剖析,从剖析的过程中得到函数的特点,运用图示加深学生对函数概念的理解.其实在我国,虽然在教材中已经删去了图示的内容,但教师在实际教学的过程中也是经常通过类似于上面的图示来加深学生对函数概念的理解,而且笔者自己在教学中也发现相对于文字的形式,学生对图示的形式更容易接受.
3 “函数”本质的分析
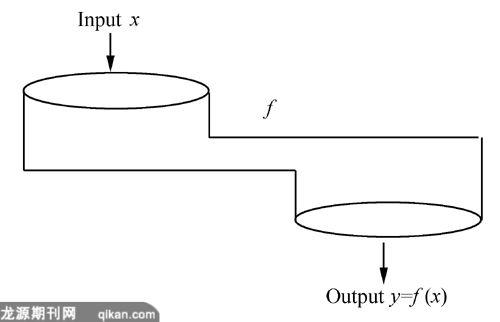
从对“函数”本质的剖析上分析,笔者觉得美国教材对函数本质的剖析更显深刻.我国的教材在给出函数概念后就给出了两个例题,而美国的教材在介绍了函数的概念后,花了很大的篇幅来逐步揭示出函数的本质.比如教材中使用了这样一个例子来强化函数概念:Sometimes it is helpful to think of a function f as a machine that receives as input a number from the domain, manipulates it, and outputs the value. See Figure.
The restrictions on this input/output machine are as follows:
1. It only accepts numbers from the domain of the function.
2. For each input, there is exactly one output (which may be repeated for different input).
Example 7 是Determining Whether an Equation Is a Function(判断等式是否是函数关系),教材给出这样的一个等式,并做出了如下解释:For values of x between -1 and 1, two values of y result. This means that the equationdoes not define a function.
Example 9 是 Identifying the Graph of a Function. 给出四张图象,让学生判断这些图象是否是函数图象.
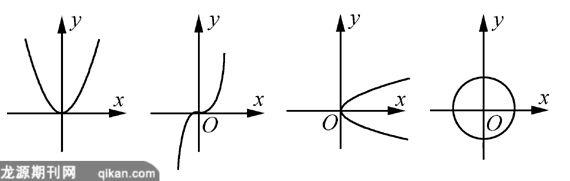
教材对于这个例题给出了Solution,引导学生从图象上加深对函数概念的理解.紧接着教材就对函数图象再作深入探讨:If (x,y) is a point on the graph of a function f, then y is the value of f at x; that is , y=f(x). The next example illustrates how to obtain information about a function if its graph is given. Example 10 就是Obtaining Information from the Graph of a Function. 给出已知函数的图象,让学生通过函数图象来研究函数的性质,比如定义域、值域、求函数值、或是已知函数值求自变量x的值等问题.函数图象在我国的教材中也有介绍,在第二节中专门介绍函数的表示法:解析法、图象法、列表法,并且通过两个例题要求学生画出分段函数的图象.
4 “函数”的表述形式
在美国的教材中对函数有一种表述形式,有别于我国的高中教材.We may think of a function as a set of ordered pairs (x,y) in which no two distinct pairs have the same first element. The set of all first elements x is the domain of the function, and the set of all second elements y is its range. Associated with each element x in the domain, there is a unique element y in the range. Example 3 is Determining Whether a Relation Represents a Function.
Determine whether each relation represents a function. For those that are functions, state the domain and range.
(a){(1,4),(2,5),(3,6),(4,7)}
(b) {(1,4),(2,4),(3,5),(6,10)}
(c) {(-3,9),(-2,4)(0,0),(1,1),(-3,8)}
In Example 3(c), this relation is not a function because there are two ordered pairs (-3,9) and (-3,8) that have the same first element, but different second elements. 这种“a set of ordered pairs (x,y)”的函数表述形式其实也是从另一种角度来加强学生对函数概念的理解.
笔者总结美国的教材,它总共从四个角度的表述形式对函数的概念与本质进行阐述:从图示的角度、从有序实数对的角度、从双变量等式的角度、从图象的角度.在我国的教学中笔者也发现学生对函数的概念理解确实存在困难,由于概念本身比较抽象,即使在一堂课上学生接受了函数概念,但在继续学习了大量关于函数的知识后,还是有一部分学生对函数概念的本质仍然含糊不清,比如在高三的总复习时曾遇到过这样一道题目:函数图象与直线x=1会有几个交点?此题的错误率非常之高,高三学生在此题上出错就说明学生虽然一直在解有关函数的问题,甚至是一些高难度的综合问题,但他们其实对函数真正的本质还未能领悟透彻.这样的现象是不是应该引起我们教师的重视,是不是我们对函数概念剖析得不够深刻,或是花费的时间还不够呢?笔者觉得我们不妨在我们自己教材的基础上,参照美国教材的一些做法,从不同的角度让学生理解函数的概念,这样做不仅培养学生多角度、多视角的观察事物,而且也起到了强化学生认知心智的作用.
5 “函数”教学重点的侧重
在具体的函数教学过程中,笔者发现我们新课程的改革有些做法非常巧合的与美国教材的处理相一致.比如关于求“值域”的处理,美国教材明确指出:We have not said much about finding the range of a function. The reason is that when a function is defined by equation it is often difficult to find the range. Therefore, we shall usually be content to find just the domain of a function when only the rule for the function is given. We shall express the domain of a function using inequalities, interval notation, set notation, or words, whichever is most convenient.可见美国教材对函数值域是非常淡化的.在我国之前的教学中,对求函数值域的要求比较高,比如分离常数法、反表示法、图象法、Δ法、换元法等等,总体来说,求函数值域比求函数定义域要困难得多,在现在的新教材中对求函数的值域也是非常淡化了,教师在新课讲解时基本是不讲解求值域了,但是在很多的参考资料中,求函数值域还是经常出现,所以这种情况也迫使教师不得不适时的补充有关内容.
美国教材重点落在求函数定义域,求函数值,以及已知函数值求自变量等问题上,这与我国的教材是相符的,而我国的教材中还特别强调了函数的三要素:定义域、对应法则、值域.着重强调了判断两个函数是否是同一个函数.
对于函数图象作图的要求,美国学生可以使用专用的作图计算器来绘制函数图象,在这方面我国对学生函数图象作图能力的要求明显高于美国,要求学生会画出一些特定函数的图象,比如含绝对值的分段函数图象.
此外在实际问题的处理上,两国的教材也有相通之处.两国的教材中有很多例题都是以实际问题为背景的,由此说明两国都很注重数学知识的实际应用,而非只拘泥于函数抽象的概念.
通过以上美国与我国教材中对“函数”概念教学的比较来分析,“函数”这个概念无论在我国还是在美国都是处于非常重要的地位,我国的新教材高一第一册几乎全部是围绕有关函数问题展开的教学,美国教材中至少7节的内容与函数有关,所以两国都非常重视“函数”概念的教学,相对比较而言,美国教材对概念剖析更详细与深入些,在多个Examples之后都从不同的角度阐明“函数”的主要特征,而我国的教材设计则在让学生自我思考与探究方面花费了一番心思,巧妙的设计了几个思考点发挥学生自主探究的能力,充分显示了“以生为本”的教学新理念.最后值得一提的是,在美国教材每节开头都有一个“Field Trip to Motorola”,在其中会有一些“Real Mathematics at Motorola”、“Interview at Motorola”,这样不仅是对学生的一种激励,更让学生感受到数学的实用价值;我国教材每一章开头也有引言或是一些引入性的情境问题,目的也是充分调动学生的学习积极性.总之在我国高中数学新课程实施的初始阶段,通过研究国外数学教材的途径,我们可以发觉很多值得我们思考的问题,获得更多改进与完善的空间.
作者简介 俞昕,出生于1977年10月,中教一级.研究方向:数学教学.取得的科研成果:课题《新课标视角下探寻高中数学课程中的文化因素》荣获市优秀科研成果一等奖.
