有趣的计数问题
2008-03-07王晓梅
王晓梅
关于m个球队进行单循环比赛时总的比赛场数n的公式是七年级数学中有名的“单循环”比赛问题。每个球队都和其他球队赛一场,共赛(m-1)场,则m个球队总共赛m(m-1)场,但是每两个球队之间只需赛一场,上面的比赛场次重复计算一次,故总比赛场次是:n=m(m-1)/2。这个结果在七年级几何计数问题中有许多有趣的应用。
1计点的个数
例1三条直线相交最多有几个交点?四条直线相交最多有几个交点?
分析:把三条直线视为三支球队,因为两条直线相交只有一个交点,因此任意一点可看成任何两个球队进行的一场比赛,则三条直线相交最多有3×(3-1)/2=3个交点,同理四条直线相交最多有4×(4-1)/2=6个交点。
推广平面内n条直线相交最多有n(n-1)/2个交点。
2计线段的条数
例2在一条直线上画4个点,共有条线段。画2007个点共有______条线段。
分析:把A、B、C、D这四个点视为4支球队,任何两点间的线段看作任意两支球队进行的一场比赛,则图中线段的总条数为4×(4-1)/2=6;画2007个点时有2007×(2007-1)/2=4026042条线段。
推广一条直线上的n个点共可组成n(n-1)/2条线段。
3计直线的条数
例3有四个点,其中任意三点都不在同一条直线上,过其中每两个点画直线,可以画几条?
分析:把四个点视为4支球队,因为过两点有且只有一条直线,因此,过任意两点的直线可看成任意两支球队进行的一场比赛,则过四个点可画4×(4-1)/2=6条直线。
推广平面内有n个点,每三个点都不在同一条直线上,过其中两点画直线,共可画出n(n-1)/2条。
4计角的个数
例4如图1共有______个角,如图2共有______个角(指0°~180°之间的角)。
分析:因为每两条射线组成唯一的一个角,所以任何两条射线组成的角,可以看成任意两支球队进行的一场比赛。
因此图1中射线组成的角的个数为4×(4-1)/2=6。
图2中射线组成的角的个数为50×(50-1)/2=1255。
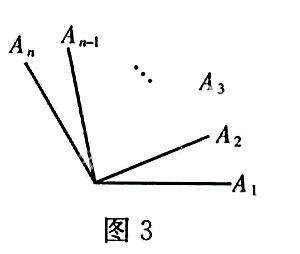
推广如图3。过0点的n条射线可组成n(n-1)/2个角。

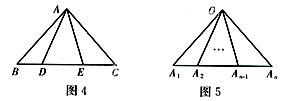
5计三角形的个数
例5图4中有几个三角形?
分析:把点B、D、E、C视为四支球队,任意两点和A点可组成唯一的一个三角形,因此任意两点和A点组成的三角形可以看成任意两支球队进行的一场比赛,所以图4中有
4×(4-1)/2=6个三角形。
推广如图5,直线上A1、A2,…。An共n个点和直线外一点0,可组成n(n-1)/2个三角形。
