深水系泊系统静力特性快速计算方法研究*

张火明1 范 菊2 杨建民2

1．中国计量学院计算机软件及理论研究所 杭州 310018 2．上海交通大学海洋工程国家重点实验室 上海 200030

深水系泊系统静力特性快速计算方法研究*

张火明1 范 菊2 杨建民2

1．中国计量学院计算机软件及理论研究所 杭州 310018 2．上海交通大学海洋工程国家重点实验室 上海 200030

为研究深水系泊系统静力特性，以工作水深为320 m的转塔式浮式生产存储系统为例，首先计算出每种类型锚泊线的水平张力TH-水平跨距X曲线、上端系缆点水平移动距离、每根锚泊线新的水平跨距，插值求出此时的每根锚泊线水平张力，投影合成后即得上端系缆点移动后的系泊系统X方向水平恢复力，垂直方向的恢复力计算方法与此类似。相应计算结果与Dynfloat软件结果相吻合。

深海平台 系泊系统 静力特性

世界范围内海洋开发正在向深海进军，许多 创新研制的适用于深海开发的新型海上石油生产处理装置不断涌现［1］，其中就包括浮式生产储油轮（FPSO）、半潜式平台、张力腿式平台（TLP）、单柱式平台（SPAR）等已获得广泛成功应用的新型平台。这些海上漂浮结构物的海上定位需要通过动力定位和锚泊系统的约束来实现［2-5］。其中锚泊系统在海洋和海岸工程中的应用十分广泛，形式也多种多样，受力情况十分复杂，通常情况下无法得出解析的表达形式，而不得不采用数值分析的方法来实现［2-5］。目前研究中，对锚链系统静力分析［6-7］的方法很多，给出了很多应用程序，用于求解锚链系统的受力和变形，其计算过程一般需采用多次迭代的方法，最终找到锚链顶端受力与锚链顶端位置的关系，一般很耗机时，因此有必要考虑采用简单直观的方法。

1 锚泊线静力计算理论

1．1 锚泊线静力计算基本方程

锚泊线可由多段不同重量和尺寸的索或链组成，段与段之间可有集中质量（悬挂重锤或浮球）。方法对松弛（有剩余索链躺在海底的）和张紧的（索链全部提起其下端拉力倾斜的）两种系泊状态均适用。

图1 锚泊线上任一微段静平衡受力分析图

见图1，锚泊线上的任一微段ds及在它上面的各个作用力。

根据图1从静平衡关系可得到

从几何关系则可得到

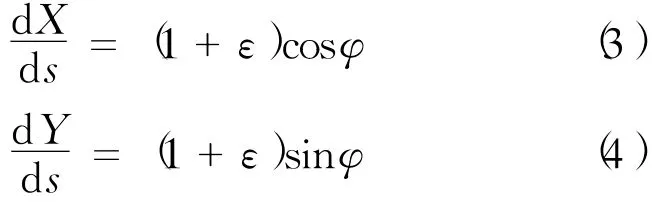
上面各式中的ε、G、F按下列公式计算

式中：A——锚泊线横截面积；

E——锚泊线材料弹性模量；

ρ——海水密度；

C——锚泊线等效直径；

CN——法向阻力系数（对圆形缆索取为1．2）；

CT——切向阻力系数，

其中：d、e——缆索形状及表面有关的系数，对圆形缆索d＝—0．035，e＝—0．035。

将式（5）～（7）分别代入式（1）～（4），便得到一组微分方程［3］，根据给定的锚泊线边界条件，对这组微分方程进行积分，即可得到沿锚泊线的各点处张力T与其倾角φ，以及各点的坐标X、Y。对这组一阶微分方程，积分方法选用适应性较强，精度较高的变步长龙格-库塔（Runge-Kutta）法［8］。

对于由多段不同重量和尺寸的索链组成的锚泊线，在进行积分时，可将前一段末端的积分结果作为相连的后一段始端的边界条件连续进行积分。若考虑流速沿水深的变化，可将流速表示成水深的函数Vc（Y），Y是锚泊线上点的纵坐标，是与水深Hw相对的，见图2。

图2 流速沿水深变化图

1．2 锚泊线静力方程定解条件

一般地，认为锚泊线静力方程式（1）～（4）存在4个定解条件［9］：给定锚泊线上端预张力；给定锚链顶端预张力倾角；给定锚泊线水平泊距；给定锚碇处的水平面坐标。

选用第1个定解条件作为求解锚泊线静力方程的初始输入，积分从锚泊线上端（浮体系缆桩处）开始逐步向下，对于浮筒和重块，将其水中重量均布在所在的积分锚泊线分段。当给定预张力后，可唯一确定锚泊线上端点的初始倾角，将其视为一个一维优化问题，采用黄金分割法［9］进行一维寻优，固定预张力，寻求最适合的初始倾角，使得到达海底时，锚链倾角最小（与海底相切，这里假设触底锚链没有全部提起，即锚泊线上端点张力没有达到极端情况），倾角取值范围设定在（0°，90°）。应该注意的是，存在一个预张力的最小值，使得锚泊线上端几乎垂直向下（初始倾角近似为90°），如果给定的预张力小于此值，锚泊线静力方程将无解。

1．3 锚泊线水平投影计算方法

对锚泊线进行静力特性计算时，当达到海底切点处停止。此时，锚泊线触底分段倾角α为0°，张力为Tb，设躺底部分锚泊线轴向刚度为AEb（对于有多个分段的锚泊线，假设仅有底部分段躺底，这在锚泊线正常工作，亦即锚泊线上端张力不过于小时一般是成立的），所受海底摩擦力为Ff，锚泊线与海底相切点横坐标为X，则，锚泊线水平投影长度为

式中：Lt——锚泊线拉伸前总长度；

Lu——锚泊线在与海底相切点以上部分拉伸前长度；

Ff——海底摩擦力，Ff＝Cfb·Wb，

其中：Cfb——海底摩擦力系数；

Wb——躺底锚链水中重量。

1．4 锚泊系统总静力特性计算方法

1）给出单根锚泊线的一系列预张力，锚泊线有几种类型，就给出几种预张力系列。对每种类型锚泊线，预张力系列范围应该包括该种类型锚泊线在所选海况作用下可能出现的张力上下限区间。预张力点数一般不能少于8个，因为随后要进行插值计算，点数太少精度不够，也不必太多，否则耗时过长，大多数情况下可选10～25个。

2）对每个给定的预张力T计算出锚泊线相应的水平跨距X和上端点倾角φ，以离散点的形式给出张力T-水平跨距X曲线、水平张力FX-水平跨距X曲线和垂直张力FZ-水平跨距X曲线，其中，FX、FZ为

3）依次给出上端系缆点水平移动距离dX（一般以系统初始静平衡时位置为0点，偏移距离可依次取为—2、—4、—6、…、—50 m，这里假设纵荡偏移范围为—50～0 m），对每个dX相应的计算每根锚泊线新的水平跨距，再根据这些新的水平跨距在对应的T-X、FX-X和FZ-X曲线中插值（插值方法选用适用性较强、精度较高的一元全区间不等间距拉格朗日（lagrange interpolate）插值法［9］）求出此时的每根锚泊线上端点张力、水平张力和垂直张力，将水平张力向X轴正方向投影，合成后即得上端系缆点移动后的锚泊系统X方向水平恢复力，垂直张力直接合成即可得上端系缆点移动后的锚泊系统Z方向垂直恢复力。完成一系列dX计算后，便可得到锚泊系统总的水平恢复力-水平偏移曲线和锚泊系统总的垂直恢复力-水平偏移曲线。对任一个dX，其计算过程可描述如下。

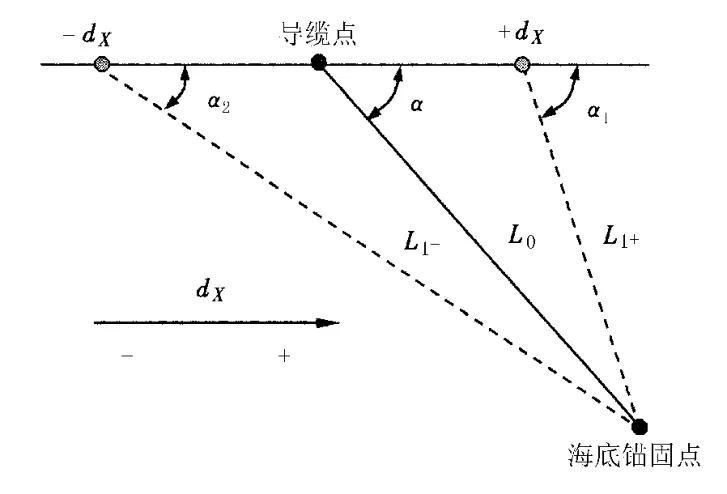
图3 锚泊总系统静力特性计算示意图

见图3，假设锚泊系统中某一根锚泊线初始水平投影长度为L0，初始布锚角为α，上端点初始倾角为φ0，系泊点向X轴正向移动dX后，相应的，该锚泊线水平投影长度（水平跨距）变为L1+，上端点倾角为φ1，根据余弦定理有

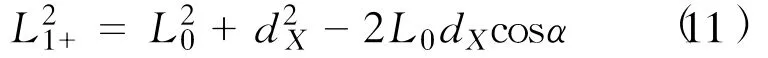
根据L1+值可插值计算出此时该锚泊线上端点水平张力FX1+和垂直张力FZ1+，再把水平张力FX1+向X轴方向投影即可得出此时该锚泊线对整个锚泊系统的水平恢复力贡献，见式（12）。

从而有

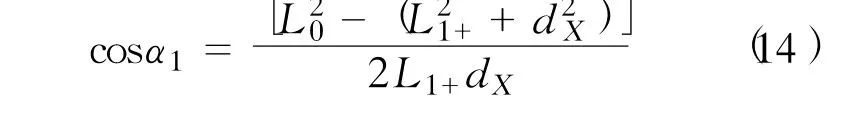
将锚泊系统所有锚泊线对整个系统恢复力的贡献叠加即可得整个锚泊系统在移动dX时的水平恢复力，如式（15）所示。

式中：n——锚泊系统锚泊线总根数；

FX+（T）——X向总恢复力；

FX+（i）——第i根锚泊线的贡献（X向分力）。

同样地，将锚泊系统所有锚泊线上端点垂直张力叠加亦可得整个锚泊系统在移动dX后的垂直恢复力，见式（16）。

式中：FZ+（T）——Z向总恢复力；

FZ+（i）——第i根锚泊线的贡献（Z向分力）。

对于本文选取的转塔式FPSO，由于其具有风标效应，因此常关心其向负向移动后的总恢复力情况，计算过程同上述方法相类似，注意此时dX为负值。

2 算例及分析

2．1 系统描述

选用工作水深为320 m的转塔式FPSO的系泊系统［8］作为研究对象。该FPSO采用内转塔式系统，包括转塔、系泊系统、立管系统3个部分，系泊系统由3组各3根共9根系泊缆组成，3组系泊缆成间隔120°均匀布置，每组3根系泊缆成5°间隔均匀布置。见图4，系泊缆数量为3×3，不考虑立管系统。

转塔主要参数和布置位置见表1。

每根系泊缆自上（与转塔连接）而下（与海底锚连接）分别由接转塔钢索、中间钢索和末端锚链这3段组成。各段钢索和锚链的具体参数与属性见表2。每根系泊缆的预张力为300 k N。

图4 转塔式系泊系统布置平面图

表1 转塔主要参数

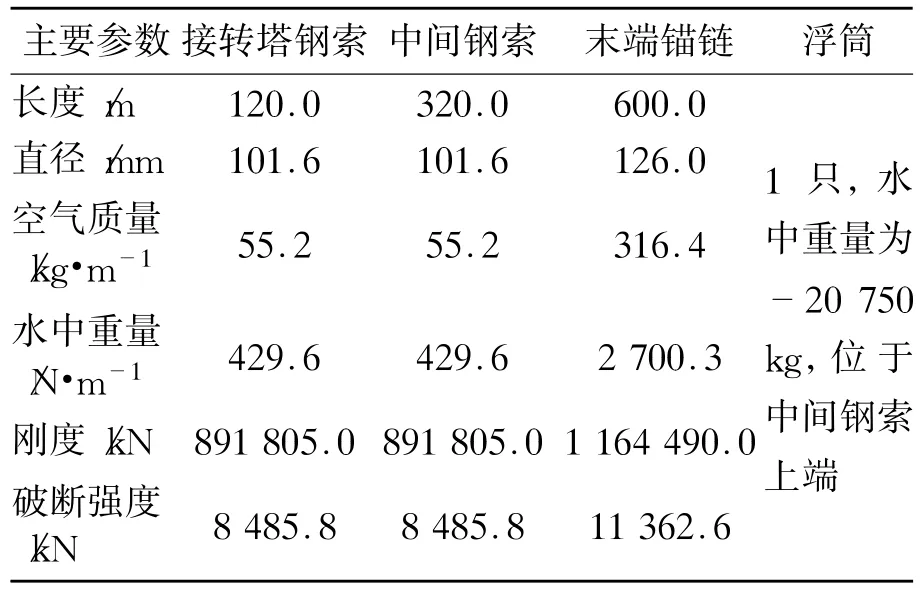
表2 320 m 水深系泊缆主要参数与属性（实际值）

2．2 锚泊系统静力计算模块的验证

荷兰Marin水池开发了一套转塔式FPSO水动力计算软件，其中Dynfloat模块可以计算转塔式系泊系统的静力特性，计算精度很好，为验证笔者所编制的转塔式系泊系统的静力特性计算模块的计算精度，现比较它和Dynfloat对320 m水深系泊系统静力特性计算结果。

计算时选取的控制参数如下：允许垂直跨距计算值与要求值误差精度εz为0．005；积分精度ε为0．000 01；锚泊线预张力T0系列点数为20，锚泊线预张力T0系列见表3；需要输出的X-T离散点数为26；水平位移增量间隔ΔX为—2．0；具有代表性的锚泊线布锚角为295°。计算时取均匀流速为0．0 m／s，纵荡偏移范围取为—50．0 m，步长取为—2．0 m，从0开始计算到—50．0 m，共26个点。

表3 320 m水深锚泊线预张力系列

图5 系泊系统静力特性计算结果比较

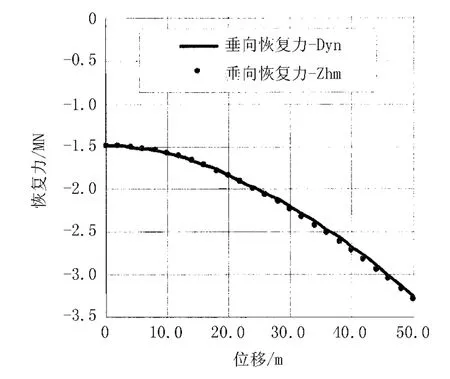
图6 系泊系统垂向恢复力特性计算结果比较

本次计算共耗时约15 s，消耗机时与水深和锚泊线长度有直接的关系，水深越深，锚泊线越长，计算时需要积分的步数越多，相应的时间也会越长。两种模块系统水平恢复力特性和单根锚泊线张力特性计算结果比较见图5，垂向恢复力特性计算结果比较见图6，考虑到绘图习惯，仍将横坐标按正值标出。

从图5、6可见，作者开发模块和Dynfloat模块计算结果十分吻合，该模块完全可用于深水系泊系统静力特性计算，其精确性是值得信赖的。

3 结语

提出一种较为简洁自然的方法求解深水系泊系统静力特性，对松弛的和张紧的两种系泊状态都适用，相应计算结果与Dynfloat软件结果吻合得很好。此方法比较简单直观，容易理解，并且耗时相对较少，比较适用于深水系泊系统静力特性计算。进一步的研究还需要效率更高，速度更快的计算方法［9］，还可以借助更好的计算机硬件系统，以缩短深水系泊系统静力特性计算消耗的时间。

［1］Rolf Baarholm，Fabio Gondim Palazzo．Hybrid Verification of a DICAS Moored FPSO［C］．Proc．of 14th ISOPE Conf．1 Toulon．France，2004：307-314．

［2］陈徐军，崔维成，沈 庆．对称式布置锚链系统的线性化处理［J］．海洋工程，2002，20（1）：75-79．

［3］潘 斌，高 捷，陈小红，陈家鼎．浮标系泊系统静力计算［J］．重庆交通学院学报，1997，16（1）：68-73．

［4］于定勇．水下锚泊系统计算［J］．青岛海洋大学学报，1995（专辑）：100-105．

［5］郝春玲，滕 斌．不均匀可拉伸单锚链系统的静力分析［J］．中国海洋平台，2003，18（4）：18-21，33．

［6］缪国平．挠性部件力学导论［M］．上海：上海交通大学出版社，1996．

［7］黄祥鹿，陆鑫森．海洋工程流体力学及结构动力响应［M］．上海：上海交通大学出版社，1992．

［8］张火明．基于等效水深截断的混合模型试验方法研究［D］．上海：上海交通大学，2005．

［9］滕 斌，郝春玲，韩 凌．Chebyshev多项式在锚链分析中的应用［J］．中国工程科学，2005，17（1）：21-26．

Investigation on quick computation method for the static characteristics of deep water mooring system

ZHANG Huo-ming1FAN Ju2YANG Jian-min2
1．School of Computer Software and Theory China Jiliang University Hangzhou 310018 2．State Key Laboratory of Ocean Engineering Shanghai Jiaotong University Shanghai 200030

A turret moored FPSOin water depth of 320m is selected toinvestigate the computational method of the static characteristics of the deep water mooring system．Firstly，the curve of horizontal tension TH against horizontal span Xis calculated and the results are expressed in discrete points．The horizontal transfer distance of the top point is presented in turn to calculate the corresponding new horizontal span of every mooring line．The horizontal tension of every mooring line is calculated by numerical interpolation in the corresponding TH-X curve according to the new horizontal span．Projecting TH at direction of X and integrating it as total，the horizontal restoring force on the top point at direction Xof the mooring system can be got．The calculation of the vertical restoring forceis similar to that mentioned above．The results are compared with those from Dynfloat and the agreement is good．

deep sea platforms mooring system static characteristics

P75 TP309

A

1671-7953（2007）02-0064-05

2006-07-20

修回日期2006-09-25

张火明（1976—），男，博士，讲师。

*国家自然科学青年基金资助项目（编号：10602055）

*中国计量学院校立项目（编号：XZ0501）