滑行艇和翼滑艇在正横规则波中的线性横摇仿真研究
2007-06-01杨松林
王 义 杨松林
江苏科技大学船舶与海洋工程学院 镇江 212003
滑行艇和翼滑艇在正横规则波中的线性横摇仿真研究
王 义 杨松林
江苏科技大学船舶与海洋工程学院 镇江 212003
建立滑行艇和翼滑艇在正横规则波中的二阶线性横摇运动微分方程,并利用前苏联中央流体动力中心ЦАГИ法得到艇体阻力,利用仿真工具Matlab/Simulink建立滑行艇和翼滑艇的横摇运动、阻力及推进系统的综合仿真模型,仿真计算结果表明建立的横摇运动微分方程较为合理,并验证具有前置V型割划式水翼的翼滑艇其横摇自稳特性要比同等吨位的滑行艇优良许多。
滑行艇 翼滑艇 横摇运动 仿真
迄今为止,国内外关于常规排水型船舶在静水和波浪中摇荡运动的研究,无论试验方法还是理论计算方法都基本上已经成熟[1-7]。由于像滑行艇和翼滑艇这类靠动升力支持艇重的高速艇,其航行过程中的航态和水动力情况不仅与常规排水型船舶完全不同,而且与高速排水型艇(即过渡型快艇)亦有本质的区别。滑行艇在滑行过程中、翼滑艇在翼滑过程中的恢复力矩直接与艇底的水动力分布及翼滑艇前置V型割划式水翼的水动力分布情况有关。目前,人们研究滑行艇和翼滑艇的摇荡特性、确定摇荡方程各系数大都采用试验的方法[8-9],未见关于滑行艇和翼滑艇在波浪中的横摇运动二阶微分方程的研究。因此,试图采用滑行面理论和三元机翼理论,推导出滑行艇在滑行、翼滑艇在翼滑状态下,正横规则波中的线性横摇恢复力矩计算式,进而得到横摇运动二阶线性微分方程,并探讨利用Matlab/Simulink的积分模块来求解该微分方程式。
1 线性横摇微分方程的建立
1.1 滑行艇横摇运动微分方程的建立
1.1.1 横摇惯性力矩M(¨φ)的计算
根据自由横摇的近似固有周期计算公式[10],可以反求横摇总转动惯量Jφφ+ΔJφφ,进而得到滑行艇横摇惯性力矩M(¨φ)为
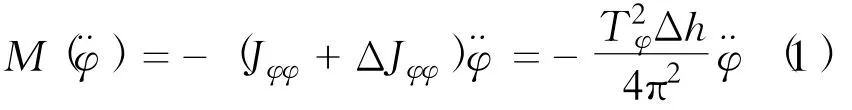
式中:Tφ——小艇(100 t以下)横摇固有周期,一般为3~5 s;
Δ——艇重,k N;
h——初稳性高,m。
1.1.2 横摇阻尼力矩M(˙φ)的计算
快艇的横摇阻尼系数的确定方法到目前为止,仍是采用试验,而且还仅是在静水中的横摇阻尼。因此滑行艇横摇阻尼系数2Nφφ的计算,借用常规船舶静水中的横摇阻尼系数的半经验或试验的方法。滑行艇的横摇阻尼力矩M(˙φ)为
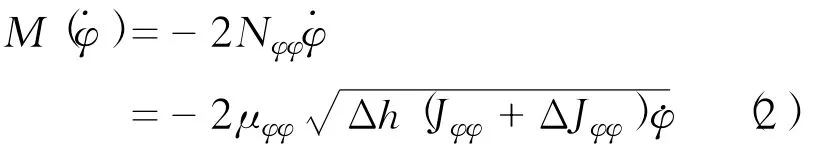
式中:2μφφ——无因次衰减系数,取为0.13。
1.1.3 横摇恢复力矩M(φ)的计算

图1 滑行艇横摇恢复力矩计算
由于艇在倾斜后,艇底两舷相对于水平面的横向斜升角β将发生变化,见图1,相当于左舷的斜升角增大为β1=β+φ,右舷的斜升角减小为β2=β—φ。由于β1>β2,根据滑行原理可知,左舷的水动力将小于右舷,艇底两侧的水动力一增一减构成恢复力矩,使艇有可能恢复至原始平衡位置[11]。可以得到滑行艇的横摇恢复力矩计算式
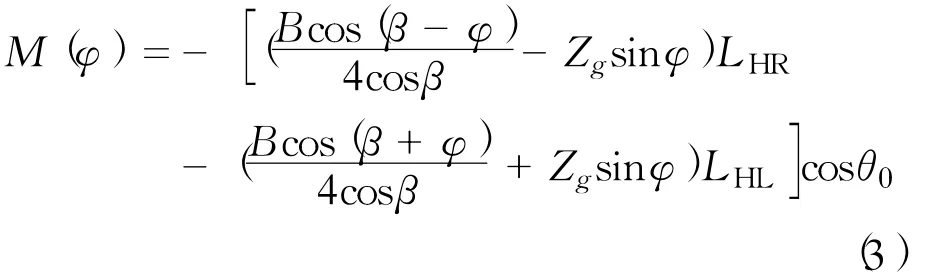
式中:LHR——艇右舷的升力,N;
LHL——艇左舷的升力,N;
θ0——航行纵倾角,(°);
Zg——艇重心垂向高度,m。
1.1.4 横摇波浪扰动力矩MW的计算
仅考虑横摇波浪主扰动力矩,参照常规船舶横摇波浪主扰动力矩的计算方法,可以得到滑行艇横摇波浪主扰动力矩MW的一般表达式

式中:Xφ——波面(倾)角修正系数;
α0——波倾角振幅;
μ——航向角,正横波为90°;
ωe——遭遇频率,正横浪时与波的真实频率相等。
1.1.5 滑行艇在正横规则波中的横摇运动微分方程1.2 翼滑艇横摇运动微分方程的建立
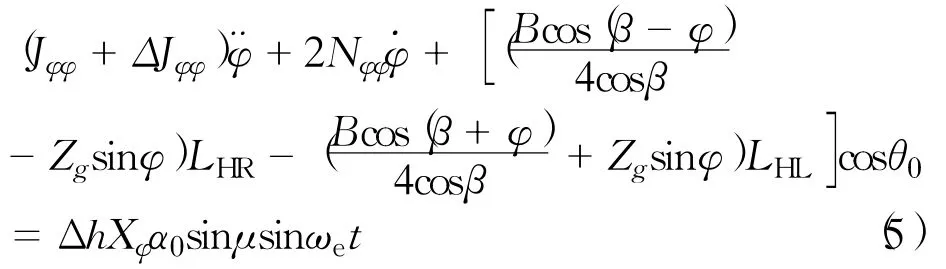
翼滑艇横摇惯性力矩、阻尼力矩和波浪主扰动力矩的计算方法采用与滑行艇相同的方法。
1.2.1 横摇恢复力矩MY(φ)的计算
与滑行艇横摇恢复力矩的分析方法类似,翼滑艇在倾斜后,艇底两舷相对于水平面的横向斜升角β将发生变化,前部V形割划式水翼的左右两侧相对于水平面的上翻角σ将发生改变,改变的量与艇两舷相同,见图2。这样,翼滑艇的滑行面和水翼产生方向相同的力矩,两力矩的合力矩即为翼滑艇横摇恢复力矩MY(φ)。

图2 翼滑艇横摇恢复力矩的计算图示
1.2.2 翼滑艇在正横规则波中的横摇运动微分方程

式中:LMR——艇右侧滑行面的升力,N;
LML——艇左侧滑行面的升力,N;
lh——单侧水翼升力的有效展长(单侧水翼在φ=0时的水平投影),m;
σ——V形割划式水翼的上翻角,(°);
ZH——水翼支柱长度,m;
LYR——右侧水翼的升力,N;
LYL——左侧水翼的升力,N。
2 滑行面及水翼动升力的计算
分别运用滑行面和三元机翼理论来计算艇底和水翼的升力,限于篇幅,仅将其计算表达式给出,升力系数表达式见文献[12]。
滑行面和水翼升力计算式为
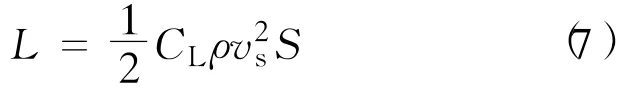
式中:CL——升力系数;
ρ——(海)水密度,kg/m3;
vs——航速,m/s;
S——升力面积,m2。
3 滑行艇和翼滑艇阻力及推进模型的建立
3.1 阻力模型
应用滑行平板资料估算滑行艇的裸艇体阻力,将艇阻力分成剩余阻力和摩擦阻力两部分。利用前苏联中央流体动力中心ЦАГИ法求艇的湿面积ST、湿长度lT和航行纵倾角(即冲角)θ0。
使用该方法需要查力矩关系曲线和动载荷系数关系曲线[13],为了便于仿真模型实时调用这些数据,本文利用曲线拟合的方法,得到函数关系式λ=f(FNB)。利用Matlab编制函数库,就可以得到在不同航速vs情况下(即不同的FNB)对应的湿长宽比λ。
翼滑艇艇体阻力计算方法与滑行艇相同,但需另外计及前置V型割划式水翼的阻力,可以参考水翼艇计算水翼阻力的方法,这里不再赘述。另外,由于滑行艇和翼滑艇的航速都较高,其附体阻力不可小视。文中采用附体阻力百分数法,取裸艇体阻力的一个百分数,取法不一,视附体多少情况而定。
3.2 螺旋桨推进模型
螺旋桨是高速艇最常用的推进器,其优点是效率高、构造及工作简单。
螺旋桨有效推力为
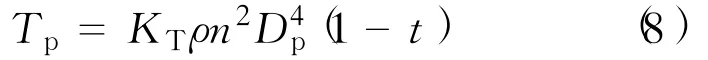
式中:KT——推力系数;
Dp——螺旋桨直径,m;
n——转速,r/s;
t——推力减额分数。
3.3 阻力和推进仿真模型
该推进系统的仿真模型是在平动方程的基础上建立的。
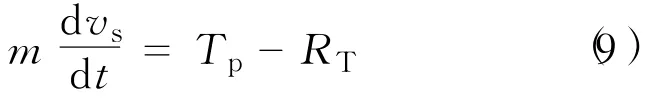
式中:m——艇质量(含附加质量),kg;
Tp——推进器有效推力,N;
RT——艇的总阻力,N。
4 算例
利用Matlab/Simulink[14]建立的滑行艇和翼滑艇横摇运动、阻力及推进综合仿真模型分别见图3、4。
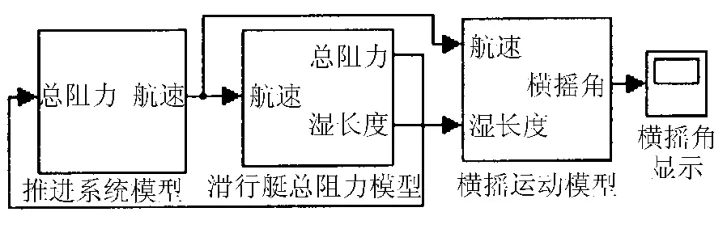
图3 滑行艇综合仿真模型
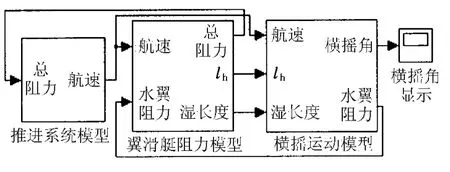
图4 翼滑艇综合仿真模型
利用Matlab仿真工具Simulink来求解滑行艇和翼滑艇横摇运动微分方程。利用Simulink积分模块来构造微分方程求解模型的核心思想是:x″经积分作用得到x′,x′再经积分模块作用就得到x,而x′和x经代数运算又产生x″,这里的x刚好对应横摇角φ。
选取吨位及尺度相同的滑行艇和翼滑艇作为算例,进行仿真对比研究。两艇的主尺度及船型参数见表1。

表1 1.4 t滑行艇及翼滑艇主尺度及船型参数
翼滑艇安装了水翼,重心位置比滑行艇偏前,为Lg=2.52 m,其他参数与滑行艇相同。算例中滑行艇实测横摇固有周期Tφ=1.1 s,翼滑艇实测横摇固有周期Tφ=1.4 s。
螺旋桨及波浪参数见表2。

表2 螺旋桨及波浪参数
仿真时间设定为100 s,运行仿真程序,得到滑行艇和翼滑艇横摇角变化曲线,见图5。
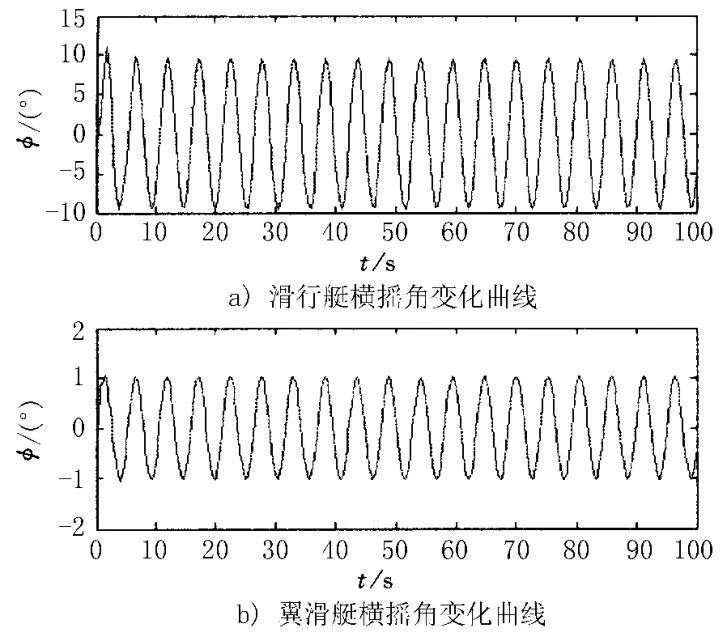
图5 滑行艇和翼滑艇横摇角变化曲线对比
该海况条件下滑行艇的横摇角幅值为9°,而翼滑艇的横摇角幅值为1°,验证了安装有V型割划式水翼的翼滑艇其横摇运动特性明显优于同等吨位的滑行艇。
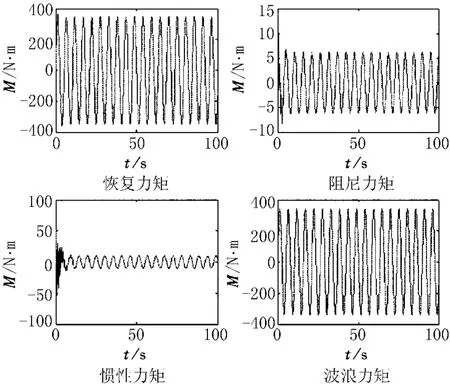
图6 翼滑艇各横摇力矩变化曲线
图6显示了翼滑艇上述海况条件下各横摇力矩的变化情况。从图6中可以看出,翼滑艇在翼滑状态下遭遇正横规则波影响时,由于其较高的航速,产生的恢复力矩是抵抗波浪力矩的最主要部分。各力矩随横摇角的正负对称变化,未发生数值的偏向,说明了利用滑行平板理论和机翼理论建立的求解翼滑艇和滑行艇的恢复力矩模型合理。
5 结论
对于滑行艇和翼滑艇这样在航行过程中靠动升力支持的快艇,在计算横摇力矩时与常规排水型船舶有着本质的区别。利用文中提供的方法可以方便地求解各力矩,特别是恢复力矩。同时由于翼滑艇前端安装了割划式水翼,其横摇自稳特性比滑行艇优良许多。另外,利用Matlab/Simulink积分模块来求解微分方程是一种非常新颖、可靠,而且适用面很广的方法,能够为研究船舶这样的复杂系统提供很好的思路。
[1]林 焰,纪卓尚.船舶在波浪中的横摇运动及其稳性[J].中国造船,1993,33(6):36-46.
[2]Nayfeh A H,Sanchez N E.Stability and complicated rolling responses of ships in regular beam seas[J].International shipbuilding progress,1990:37.
[3]余 音,胡毓仁,金咸定.船舶在波浪中的非线性横摇研究的现状和发展[J].船舶力学,2000,4(1):73-77.
[4]袁 远,成志军,金咸定.船舶在波浪中运动的六自由度非线性耦合方程[J].上海交通大学学报,2001,35(4):541-543.
[5]陶尧森,冯铁城,丁 皓.舰船优化设计中耐波性计算方法的探讨[J].船舶力学,2000,4(2):6-9.
[6]李远林,吴家鸣,王冬姣.波浪对船舶非线性横摇阻尼的影响[J].船舶工程,2003,25(2):21-24.
[7]李远林,伍晓榕.非线性横摇阻尼的试验确定[J].华南理工大学学报:自然科学版,2002,30(2):79-82.
[8]董文才,黄祥兵,刘志华.深V型滑行艇横摇阻尼的实验确定[J].海军工程大学学报,2004,16(4):26-29.
[9]王小宁译.滑行艇动稳性[J].国外舰船工程,1998(5):11-18.
[10]李积德.船舶耐波性[M].哈尔滨:哈尔滨船舶工程学院出版社,1992:34-42,47-50.
[11]蒯挺适.军用快艇设计基础知识[M].北京:国防工业出版社,1992:56-57.
[12]奚 炜.翼滑艇运动智能控制仿真初步研究[D].镇江:江苏科技大学,2006:34-35,41.
[13]邵世明,王云才.高速艇动力学[M].上海:上海交通大学出版社,1990:90-93.
[14]张志涌.精通MATLAB 6.5版[M].北京:北京航空航天大学出版社,2003:366-384.
Study on linear rolling simulation of the planing craft and hydrofoil-planing craft in regular beam waves
WANG Yi YANGSong-lin
School of Naval Architecture and Ocean Engineering Jiangsu University of Science and Technology Zhenjiang 212003
Two order linear differential equations of rolling motion for the planning craft and hydrofoil-planing craft are established.TheЦАГИmethod is used to calculate the resistance of craft,and the overall simulation models of rolling,resistance and propulsion are built by Matlab/Simulink.Numerical examples and simulations′show that the rolling differential equations are reasonable,and proved that the rolling self-stability of a hydrofoil-planing craft with V type hydrofoil is much better than that of planing craft.
planing craft hydrofoil-planing craft rolling simulation
U674.94
A
1671-7953(2007)02-0013-04
2006-09-18
修回日期2006-11-06
王 义(1981—),男,硕士生。
