锚泊阻尼研究综述
2015-05-06陈佳欣
杨 勇,尹 群,陈佳欣
(江苏科技大学船舶与海洋工程学院,江苏镇江212003)
0 引言
海洋结构物在服役期间所承受的环境载荷作用主要是由风、浪、流、潮汐、地震等因素引起的,其中风载荷、流载荷和波浪载荷对结构物的影响较大,在设计过程中需要进行重点考虑[1]。在这些载荷的作用下,海洋浮式结构物往往会产生较为复杂的运动响应,主要包括:(1)流载荷、平均风载荷、二阶波浪平均漂移力引起的平均静力位移;(2)一阶波浪力引起的波频振荡运动;(3)二阶慢漂波浪力、随机风载荷、二阶锚泊线力引起的低频振荡运动。
由于低频振荡运动的频率与结构物系统的固有频率较为接近,因此会产生大位移的共振低频慢漂运动,但过大的位移对于平台的正常作业会产生不可预估的后果。移动式钻井平台必须保证其运动位移不超过钻探作业所允许的最大运动幅度[2],通常认为半潜式钻井平台的移动半径不能超过水深的5%。对于如何限制海洋平台慢漂运动位移幅度这个问题,整个系统能够提供的阻尼值将会起到重要的作用。相关研究发现[3],锚泊线提供的阻尼最大可以占到系统总阻尼的80%。
过去很长一段时间内通常认为在预测系泊式海洋结构物的运动响应时,锚泊阻尼作用是可以忽略的,锚泊系统对浮体最主要的作用是其所提供的回复力,导致这一误解的最主要原因是锚泊线的拖曳面积与平台本身相比是十分小的,几乎可以忽略。Huse[4]发现锚泊阻尼在结构物发生一阶波频振荡运动时,对结构物运动的影响的确是十分有限的,但是对于二阶低频振荡运动,锚泊阻尼能够大大降低其运动能量。因为在一个低频运动周期内,锚泊线单元在垂直于其自身切线方向上运动的振幅远远大于平台自身的运动振幅,因此,锚泊阻尼研究对准确预计结构物的运动响应和进行合理有效的锚泊系统设计有着重要的工程意义。
1 时域全动态有限元法
1.1 指示图法与等效线性阻尼系数
时域全动态有限元法被广泛应用于锚泊阻尼的计算与研究中。通过相关的商业有限元软件进行建模、仿真以及计算,得到一个低频振荡周期内锚泊线顶端张力的水平分量,并作为一个时间历程输出,将其与锚泊线顶端运动的低频水平速度分量相乘,并在一个运动周期内积分,从而得到锚泊线在一个振荡周期内耗散的能量值,这一求解过程通常通过指示图法来完成。图1是典型指示图法的示意图,以锚泊线顶端运动的水平位移为横坐标,锚泊线顶端张力的水平分量为纵坐标,两者围成曲线的面积代表一个振荡周期内锚泊线所消耗的能量[5]。
锚泊线在顶端结构物一个振荡运动周期内所耗散的能量E可以通过以下公式来计算:

式中:Th为锚泊线顶端张力水平分量;X为锚泊线顶端水平位移;dX/dt为锚泊线顶端移动速度;τ为锚泊线顶端振荡周期。

图1 指示图
引入等效线性阻尼系数B,锚泊线顶端张力水平分量Th可以表示为:

将式(2)代入式(1),可以得到:

假设锚泊线顶端运动是一个周期为τ、振幅为a的正弦运动,带入式(3)可解得:

式中:a为锚泊线顶端正弦运动振幅;τ为锚泊线顶端正弦运动周期。
因此,锚泊线等效线性阻尼系数B可以表示为:

式(5)中能量E由图1中曲线围成的面积计算得到。
1.2 方法应用与研究现状
Webster[5]用完全时域非线性动态有限元法同时结合指示图法相关理论对锚泊阻尼进行了无量纲分析。通过研究发现,锚泊线的预张力、拖曳力系数和刚度对锚泊阻尼有着十分重要的影响。随着这些参数的增加,锚泊阻尼先呈现出先上升后下降的趋势,而海流速度对锚泊阻尼的影响较小,且随着流速的增加,锚泊阻尼几乎不变。
Brown 和 Mavrakos[6]对 15 所大学与研究机构的有限元计算结果与实验进行了比较研究,发现基于时域分析的有限元方法能够更加准确可靠地得到锚泊线的顶端张力值,从而得到准确的锚泊阻尼结果。Brown和Mavrakos对叠加波频运动后的低频锚泊阻尼特性进行了比较分析,根据文中算例结果,单一钢链形式锚泊线在叠加波频运动后,原来低频运动下所具有的锚泊阻尼值会扩大7至8倍,而单一钢索形式锚泊线在叠加波频运动后,锚泊阻尼虽然增大没有这么多,但也是原来的2倍多,可见波频运动对锚泊阻尼的影响是十分显著的。
Johanning,Smith 和 Wolfram[7]采用时域有限元法研究了锚泊线的轴向拉伸和顶端运动动态变化对锚泊阻尼的影响,锚泊线顶端运动为单一的简谐运动,结果显示锚泊阻尼受它们的影响较大。
上海交通大学的苏志勇等[8]选取一组工程中常用的锚泊参数,研究了锚泊线顶端运动为单一简谐运动时各个参数对锚泊水平阻尼和垂向阻尼的影响,结果显示轴向刚度和顶端运动方程对锚泊阻尼的影响较为显著。
哈尔滨工业大学的乔东升等[9]用有限元方法对锚泊线进行非线性时域动力分析,分析了海流速度以及海底摩擦系数对锚泊阻尼的影响。研究发现海底摩擦系数对锚泊阻尼的影响十分的有限,而海流速度会导致低频振荡运动下锚泊阻尼值的增加。研究还表明,随着顶端简谐振荡运动周期的减少和振幅的增加,锚泊阻尼呈现上升趋势。
2 准静态分析法
2.1 Huse模型
准静态分析法适用于锚泊线顶端运动十分缓慢的情况,即锚泊线顶端处于低频振荡运动。假设锚泊线在结构物一个运动周期内时刻都处于准静态状态,利用悬链线方程计算得到锚泊线在平衡位置以及2个最大振幅位置时的各个锚泊线单元节点的位置坐标,从而利用相关公式进行推导计算得出锚泊线在一个运动周期内消耗的系统能量和锚泊线等效线性阻尼系数[10]。
锚泊阻尼研究准静态分析法首先由Huse[4]提出,通过计算作用于锚泊线上的拖曳力所消耗的系统能量,得到锚泊线等效线性阻尼系数。基于准静态法计算模型,通过改变锚泊阻尼研究中一些主要系统参数的大小,进行系统性分析计算,Huse[11]编制了一个系列图表用于锚泊阻尼的直接计算。
准静态分析法中,锚泊线在一个运动周期内耗散能量的计算推导过程如下所叙述。假设锚泊线顶端的运动是一个正弦振荡运动,其运动振幅为a0,运动周期为τ,运动方程可以表示为:

式中:a0为锚泊线顶端正弦运动振幅;ω为锚泊线顶端正弦运动角频率。
同时,假设锚泊线单元ds在垂直于其切线方向的运动是振幅为n0(如图2所示)的正弦运动,运动周期同样为τ:

式中:s为沿曲线的坐标;n0(s)为锚泊线单元ds在垂直于其切线方向的运动振幅。
图2 中,TP1、TP2分别为锚泊线顶端运动到近端位置和远端位置时(2个最大振幅处)的海底触点位置;ΔZ为锚泊线单元ds在一个运动周期内的最大垂向位移;ΔX为锚泊线单元ds在一个运动周期内的最大水平位移;θ为锚泊线顶端运动到中间平衡位置时,锚泊线单元ds切线和水平方向的夹角。
平行于锚泊线切线方向的拖曳力被忽略掉。根据莫里森方程,垂直于锚泊线切线方向的拖曳力可以表示为:

式中:ρ为水密度;D为锚泊线等效直径;C为垂向拖曳力系数;˙n对式(7)等边式右边求导。
锚泊线单元在一个运动周期内所消耗的能量是作用在其上的拖曳力所做的功,可以推导得到:
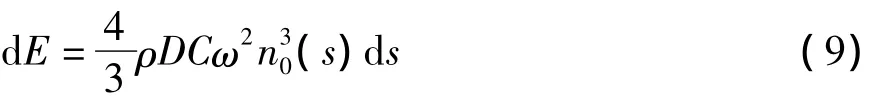
因此,作用在锚泊线上的拖曳力所造成的能量耗散与锚泊线运动振幅的三次方成正比。同时,运动位移的表达式为:

考虑到与锚泊线单元的垂向运动分量相比,其水平运动分量可以忽略,因此式(10)可以近似成:

将式(11)带入到式(9)中,可以得到:

沿着整条锚泊线进行积分得到能量E之后,再利用式(5)进行计算,从而得到锚泊线的等效线性阻尼系数。
2.2 Liu模型与Bauduin模型
在实际应用中,考虑到悬链线方程自身的几何非线性,在一个完整运动周期内,锚泊线单元的运动位移对于中间位置并不是完全对称的。因此,Liu提出了一个更为准确的计算方法,将一个完整的运动周期分为2个周期来分别计算,将2个不对称振幅分别进行考虑。
基于Liu对准静态分析法的改进,Bauduin和Naciri[12]将整个运动周期分成N(N≧8)个阶段,同时考虑了锚泊线单元在一个运动周期内平行于自身切线方向的位移对其运动的贡献,提出了一个更为精确的锚泊阻尼计算方法。
3 模型实验法
3.1 自由衰减实验
自由衰减实验法是最早用于测量锚泊阻尼的实验方法,通过将浮体与锚链的整体模型移动到一定的距离并加以释放,使其自由移动,观察并记录其振幅衰减的变化,从而得到系统的总阻尼。但是,自由衰减实验法对锚泊阻尼之外的系统阻尼的测量十分困难,只能近似估算。通常情况下,锚泊阻尼取为系统总阻尼的60%至80%。
Huse[4]利用2个半潜平台模型进行了实验。每个模型都分别进行2组实验。第1组是连接完整的锚泊系统模型,第2组是用合适刚度的横向水平弹簧代替,仅仅模拟锚泊系统对模型的回复力作用。实验结果显示,2个模型通过2组不同方式的锚泊,低频运动幅值分别被衰减了25%和20%,被减少的振幅考虑来自于锚泊系统的阻尼作用。但是当模型处于波频运动范围时,2组结果差别不大。
Bauduin和 Naciri[13]比较了改进后准静态分析法的结果和衰减实验所得的结果,得到了比较满意的对比结果。衰减实验中,通过系统总阻尼减去粘性阻尼得到锚泊阻尼。粘性阻尼是利用模型连接水平弹簧进行实验得到,总阻尼由模型连接完整锚泊系统进行实验得到。
Johanning,Smith 等[7]利用衰减实验研究了锚泊阻尼,并探究了预张力对锚泊阻尼特性的影响。研究结果显示,系统运动在锚泊线高预张力的情况下衰减周期会明显缩短,这也意味着预张力越大,锚泊线会消耗更多的系统能量,锚泊阻尼越大。
3.2 受迫振动实验
受迫振动实验法通常与指示图法进行结合,是目前最合适也比较准确的模型实验方法,其原理与使用动态有限元软件进行模拟计算十分相似。通过特殊装置使得浮体模型以一定的周期和振幅进行无衰减运动,测量并记录锚泊线模型顶端张力水平分量以及水平位移历程,结合指示图法算出锚泊线所消耗的系统能量,进而得到等效线性阻尼系数。
Wichers 和 Huijsmans[13]利用受迫振动实验对锚泊阻尼进行了研究。结果显示,结构物在发生低频振荡运动时,锚泊线提供的阻尼与结构物自身的粘性阻尼处于同一个数量级,都十分重要。同时,发现当结构物运动中加入波频垂荡运动后,锚泊阻尼增长显著。
Kitney和Brown[14]通过受迫振动实验发现所得到的锚泊线顶端张力数值和数值计算的结果还是较为接近的,验证了该实验方法的可行性。
4 结论与今后工作
本文主要介绍了锚泊阻尼研究的方法与成果,方法主要分为时域全动态有限元法、准静态分析法和模型实验法。在时域全动态有限元法部分,重点介绍了指示图理论以及等效线性阻尼系数的定义与推导过程。在准静态分析法部分,主要介绍了2种准静态分析计算模型,即Huse模型与Liu模型,并对计算锚泊阻尼的公式推导过程进行了介绍。在模型实验法部分,重点介绍了2种求解锚泊阻尼的主要实验方法,即自由衰减实验和受迫振动实验。本文在介绍这3大类锚泊阻尼研究方法的同时,对这些方法的应用以及研究成果进行了综述。这些研究成果可以概括为:
(1)锚泊阻尼是系统总阻尼中不可或缺的一部分,其对顶端结构物的一阶波频运动影响很小,但是对结构物的二阶低频运动却有着重要的限制作用。
(2)锚泊线顶端发生单一简谐振荡运动时,锚泊阻尼随着运动周期的减小或是振幅的增加而变大。
(3)锚泊线顶端发生单一简谐振荡运动时,锚泊阻尼受锚泊线刚度、锚泊线预张力、拖曳力系数、水深的影响较大。当简谐振荡运动频率较快时,流速改变对锚泊阻尼影响很小;当简谐振荡运动频率较慢时,流速改变对锚泊阻尼影响很大。
(4)单一低频简谐振荡运动下的锚泊阻尼值,在锚泊线顶端运动中叠加入波频简谐振荡运动后,锚泊阻尼值会大幅度的增长。
根据锚泊阻尼现有的研究成果以及各种求解方法的优劣性,今后锚泊阻尼重点研究的方向可以概括为以下几个部分:
(1)此前的研究对象大部分均为单一成分金属锚泊线,对于其他锚泊线的锚泊阻尼特性还需要进行研究,如多成分金属锚泊线、非金属锚泊线等。
(2)进一步改进锚泊阻尼计算准静态模型,提高计算的结果精度。
(3)考虑到波频随机运动可以看成无数个波频简谐振荡的合运动,这些运动之间是否存在抵消作用,而削弱对锚泊阻尼的影响,值得进行研究。
(4)鉴于时域全动态有限元法的准确性与方便性,利用该方法对复杂运动下的锚泊阻尼特性和锚泊阻尼参数影响进行研究,例如低频简谐振荡与波频简谐振荡的合运动以及低频简谐振荡与波频随机的合运动,而不只是仅仅考虑单一的简谐振荡。
[1] 李润培,王志农.海洋平台强度分析[M].上海:上海交通大学出版社,1992.
[2] 黄祥鹿,陆鑫森.海洋工程流体力学及结构动力响应[M].上海:上海交通大学出版社,1992.
[3] Huse E,Matsumoto K.Mooring Line Damping due to First-and Second-order Vessel Motion[C]//MEPC.21st Offshore Technology Conference.London:MEPC,1989:135-148.
[4] Huse E.Influence of Mooring Line Damping upon Rig Motions[C]//MEPC.18th Offshore Technology Conference.London:MEPC,1986:433-438.
[5] Webster W C.Mooring-induced Damping[J].Ocean Engineering,1995,22(6):571-591.
[6] Brown D T,Mavrakos S.Comparative Study on Mooring Line Dynamic Loading[J].Marine Structures,1999(12):131-151.
[7] Johaning L,Smith G H,Wolfram J.Measurements of Static and Dynamic Mooring Line Damping and Their Importance for Floating WEC Devices[J].Ocean Engineering,2007:1918-1934.
[8] 苏志勇,陈刚,杨建民,等.深海浮式结构物锚泊阻尼参数研究[J]. 海洋工程,2009,27(2):22-28.
[9] 乔东升,欧进萍.深水平台锚泊定位系统动力特性与响应分析[D].哈尔滨:哈尔滨工业大学,2011.
[10] Huse E.New Developments in Prediction of Mooring System Damping[C]//MEPC.23rd Offshore Technology Conference.London:MEPC,1991:291-298.
[11] Huse E,Matsumoto K.Practical Estimation of Mooring Line Damping[C]//MEPC.20th Offshore Technology Conference.London:MEPC,1988:543-552.
[12] Bauduin C,Naciri M.A Contribution on Quasi-static Mooring Line Damping[J].Offshore Mechanics and Arctic Engineering,2000,122:125-133.
[13] Wichers J E,Huijsmans R H.The Contribution of Hydrodynamic Damping Induced by Mooring Chains on Low-frequency Vessel Motions[C]//MEPC.22nd Offshore Technology Conference.London:MEPC,1990:171-182.
[14] Kitney N,Brown D T.Experimental Investigation of Mooring Line Loading Using Large and Small-scale Models[J].Offshore Mechanics and Arctic Engineering,2001,123:1-9.
