如何给能力多元的班级上数学课

吴仲和

教学背景

1.爱德华是美国加州具有7年教龄、非洲裔的初中数学和科学教师。他对数学教学的信念是，教师必须相信每一个学生都能学好数学，作为教师，重要的是给每个学生提供足够的学习机会。他还相信教育的目的不仅是教会学生应会的数学和科学基本技能，更重要的是教会学生做一个合格的公民。

2.学生情况：八年级，全班共29名学生（16男13女），其中有2个白种人，12个拉丁裔人，13个非洲裔人，2个亚裔人。英语作为第二语言的学生占25%以上。3个学生的数学成绩高于平均水平，2个学生的数学成绩低于平均水平。

3.教学内容：未知数和简单方程。授课时间：60分钟。

课例

爱德华老师首先告诉学生此课的目的以及如何达到这个目的：我们首先要复习一下预备知识，新课的内容是未知数和简单方程，我们还要阐述方程的解法和验算方程的解。

1.复习预备知识。

（1）爱德华老师的课从复习新课的预备知识（POD）开始：学生在已有格式的纸上大约用了5分钟的时间来完成下列练习题。

①求值：3y-13，当y=7时。

②求值：7w+4-w，当w=2时。

③写出代数式：比20小的数。

爱德华老师先选择3个学生在黑板上回答问题，然后让其他学生有充分的机会表达不同的答案，爱德华老师接着解释为什么有的是正确的答案，为什么其他的是错误答案。他让学生们特别观察POD的第1、2题，并特别解释求值与代入未知数的关系以导入新课的内容。

2.教授新课。

爱德华老师开始今天的新课内容。他特别强调要每个学生拿出数学笔记本来记录今天的学习内容，并确认都准备好了。

（1）设立框架打基础。

a.与实际生活相联系。爱德华老师先让学生表达“什么是等式”后，用专门用于教学的计算机投影（聪明小白板）给出了等式的正式定义，即等式是用等号连接的数学表达式。他还要求学生能够举出数学表达和日常生活中的例子，以便进一步理解等式的概念和在实际生活中的应用。他还让学生与邻座互相讨论，相互阐述等式的内容和日常生活的例子，然后随机选择学生在全班进行阐述。例如，一组学生给出表达等式，并举出与实际生活有关的例子：杰夫需要$38来购买自己需要的电子软件，他利用周末帮助邻居清除院子里的杂草。如果杰夫已有$3，清除杂草1小时可得$5，那么杰夫将工作几小时，才能有$38？

b.用实物建模来帮助学生建立直观的思维，懂得概念。当学生对直观等式的概念有了明确的理解后，爱德华老师立即用代数等式将一般等式予以升华。他举出这样的等式例子：9+2=11，x+7=37，a+（-3）=2a+5，并用代数天平秤（图2）来阐述代数等式的特点：开放等式（含未知数的等式）和两边相等，同时用3种代数式来说明代数式的特点。

爱德华老师指出天平秤的中杆相当于等式的等号，红盘子里的砝码代表正数，黄盘子里的砝码代表负数。爱德华老师用不同重量的小砝码来演示代数等式。他这样做的目的是使学生们能直观地感受代数式的意义。

●3+4是否等于5？爱德华老师将3个小砝码放入左边的红盘子里，又将4个小砝码放入左边的红盘子里，让学生们设想一下，如果他将5个小砝码放入右边的红盘子里，天平秤是平衡还是不平衡？（学生小声地议论，有的说平衡，有的说不平衡。）这时，爱德华老师在右边的红盘子里放入5个小砝码，学生们从数学天平秤可以直观地感受到天平秤不平衡。爱德华老師进一步解释为什么不平衡：因为左边是7而右边是5，其数学解释是：7≠5。

●（-2）+5是否等于-3？爱德华老师将2个小砝码放入左边的黄盘子里，再将5个小砝码放入左边的红盘子里，他让学生们设想一下，如果将3个小砝码放入右边的黄盘子里，天平秤是平衡还是不平衡？在学生们议论后，爱德华老师在右边的黄盘子里放入3个小砝码，学生们可以直观地感受到天平秤不平衡。爱德华老师进一步解释为什么不平衡：因为左边是3而右边是-3，其数学解释是：3≠-3。

●（-7）+2是否等于-5？爱德华老师用上述方式引导学生先设想，然后议论，再直观感受天平秤是否平衡，最后爱德华老师进一步解释为什么平衡。

c.建立抽象思维，用实物建模来验证抽象思维并让学生有充分的时间来练习巩固。当学生对等式有了直观的理解后，为了进一步帮助学生们建立对代数式的抽象理解，爱德华老师在黑板上写出了下列题目并移开代数天平秤，要求学生用对应的代数天平秤对这些等式的正误作出判断。

①9-7=3

②4×5=20

③3（-5）+4=11

在学生做题期间，爱德华老师来到两个低于平均水平的同学旁边，确认他们对以上内容是否跟得上和是否需要进一步的帮助。个别学生做得快的，爱德华老师或让他们帮助别人，或让他们思考一下如何用代数天平秤来展示代数等式。当全班同学都完成了课堂练习，爱德华老师除了让学生们做出解释外，自己还将所有的题都重新解释一遍，以便所有的学生都能懂得课堂上所涵盖的内容。当学生理解等式概念后，爱德华老师再一次使用代数天平秤来连接代数等式（方程式）以使学生能有直观的感受并建立抽象思维。

●（-7）+2=x，当x等于什么数时，才能使等式正确？爱德华老师将7个小砝码放入左边的黄盘子里，再将2个小砝码放入左边的红盘子里，让学生们设想一下，在右边什么颜色的盘子里放入几个小砝码才能使代数天平秤平衡？如果他将5个小砝码放入右边的红盘子里，天平秤是平衡还是不平衡？（学生小声地议论，有的说应放入红盘子里，有的说应放入黄盘子里。）在学生们议论之后，爱德华老师在右边的黄盘子里放入5个小砝码，学生们可以直观地观察到当x等于（-5）时天平秤平衡。爱德华老师进一步解释为什么平衡：因为左边是-5而右边也是-5，其数学解释是（-7）+2=-5，即x=-5。

●x+4=-2，当x等于什么数时，才能使等式正确？爱德华老师按照以上差不多的程序边放砝码，边让学生们设想答案、讨论，最后在正确的盘子里放入6个小砝码，让学生们直观地观察到，当x等于（-6）时天平秤平衡，等式正确。其数学解释是-6+4=-2，即x=-6。

d.实际应用。爱德华老师特别强调开放等式，即代数等式的重要性，并给出定义：开放等式（方程式）就是包含有一个或多个变量的等式。然后让每个学生自己创造一到两个与现实生活有联系的含有一个未知数等式的例子，并要求学生能够将他们创造的方程式与邻座的同学分享和讨论。然后，爱德华老师让学生将他们创造的含有一个未知数的方程式在全班与其他同学分享，并用学生们的实例作为讨论的基础。这里是部分学生的例子：

①w-11=34：杰克有一些铅笔，他将11支铅笔给了其他同学，还余34支铅笔，问杰克原来有几支铅笔？

②6y+3=27：珊德娜已有$3，她利用周末帮助邻居清扫院子每小时可得$6，问几小时后，珊德娜可有$27？

③x/3=12：如果一个玩具的价格是$12，问乔治需要有多少钱才能购买3个玩具？

（2）引入新的内容：解方程。

a.当确定学生们对于代数等式在概念、计算和应用三个方面有所了解后，爱德华老师这时将重点放在对方程的解上。什么是方程的解？爱德华老师让学生充分讨论，然后他归纳出方程的解的定义：方程的解是当你将其代入原方程，使得这个方程的等式成立的那个数。爱德华老师先给出简单方程解的例子：

①x+3=10，x=7是方程的解，因为7+3=10。

②110+y=115，y=15不是方程的解，因为110+15≠115。

b.爱德华老师在学生对于基本的代数等式即方程的解有比较深的理解后，将代数等式与现实生活连接起来。他一再告诉学生们不要急于求快，要等到完全懂得变量的关系后再列方程和解方程。他要求学生们将下列应用题转换成代数等式：

潜水员的设备重17kg，潜水员和设备共重89kg，问潜水员有多重？

在学生思考时，爱德华老师一再告诫学生们，他并不要求他们很快地找出答案，而是把重点放在变量关系上，从而正确地列出方程。在教室观察一圈后，他发现有的同学给出了106kg。为此，他带领学生一同分析：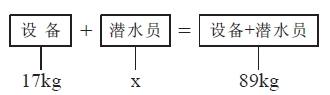

爱德华老师展示建模并找出抽象代数式的过程，指出x不可能是106kg，因为17+106≠89。

爱德华老师举出另一个例子让学生来建模、列方程和解方程：

一个容器重3kg，你的书包和容器加起来共重16.5kg，问你的书包的重量可否是13.5kg？你需要写出方程，然后解方程来回答这个问题。你可以与你的同伴一起讨论，然后由小组代表来与全班同学分享。

在这个活动中，同学们经过讨论，基本都能由直观的方框图产生出代数式，即3加上什么数能得到16.5，学生利用16.5-3=13.5，然后将解x=13.5代入3+x=16.5，得出16.5=16.5。

（3）应用。

爱德华老师让学生与相邻同学讨论并举出（或创造）一个将应用题转换成代数等式的实际例子。下面的例子是一组学生经过讨论举出的：

冰球运动员的设备和球衣重11kg，冰球运动员和他的设备以及球衣共重108kg。问冰球运动员的体重可否是99kg？

此时，学生们列方程、解方程以及检查方程的解已基本沒有问题了。爱德华老师有意识地选出几个学习能力较弱的学生来回答这个问题，他们做出了下列回答：

列方程：11+x=108

检查方程的解：将x=99代入方程得出110≠108。因此冰球运动员的体重不可能是99kg。

需要指出的是，在这个班上，无论是学习能力较强的、较弱的，还是学习能力平均的学生，都能认真地记录自己的课堂笔记。爱德华老师利用尽可能多的机会与不同学生互动，特别是对学习能力较弱的学生，更是给予尽可能多的和有意识的关心。这在无形中也起到了检查学生的作用。

3.写数学日志。

这节课最后一项教学内容是让学生写今天的数学日志。日志内容包括：日期、数学概念（变量和方程式）以及相应的数学课程标准，最后一项是书面解释：如何检查x=7是否是方程3x-10=11的解。爱德华老师要求学生们用自己的语言来阐述他们所学到的知识，并与相邻的同学交流，然后随机地抽出几个学生与全班分享他们所学到的知识。

在学生们专心地写数学日志时，爱德华老师再一次走到不同学生的面前，以便确认这些学生确实掌握了今天所教的内容。

最后，爱德华老师用抽签的方式来让3个学生在全班阐述他们的数学日志以达到总结本课内容、复习和巩固所学知识的目的。

课例评述

这是一堂普通的代数预备课。由于学生多为少数族裔，使得教课的节奏相对较慢，因为爱德华老师知道，教这样的学生不能快，否则效果会相反。尽管如此，这节课还是体现了概念、计算和应用三个方面的重点。下面用12条有效教学的内容来讨论爱德华老师的课。

（1）相关性：爱德华老师非常明确教学的目的并与课程标准相对应，即学生能够懂得未知数和简单方程的解法。教学内容与学生水平和教学目的相关。

（2）联系性：爱德华老师以学生已有的知识为切入点，并使之与新内容相联系。更重要的是，他不仅自己联系实际进行教学，还要求学生能够举出与实际生活相联系的例子来加深学生对所学知识的理解。

（3）平衡性：这节课在数学概念、熟练计算和实际应用上取得了相对平衡。从时间上统计，爱德华老师用于数学概念的时间为21分钟（35%），熟练计算上的时间为16分钟（27%），实际应用上的时间为19分钟（32%）。

（4）有序性：爱德华老师兼顾了不同层次的学生，由浅入深从预备知识到概念的引进及框架的设置；从老师的介绍到学生的创造和反馈；从学生的课堂练习到学生与老师的互动，层次分明，逻辑推理由易到难。

（5）多元性：爱德华老师的这个班是典型的多元化班级。此多元化不仅体现在种族的多元，还体现在学习能力的多元。不让一个孩子掉队是爱德华老师的目标。为此，他将精力用在了学习能力较差的孩子身上，利用一切机会来检查这些学生的进度。比如，这节课，爱德华老师利用课堂练习的机会与两个低于平均水平的学生的互动多达5次，共计使用8分钟（13%）的时间。他还对高于平均水平的学生提出新的学习要求，即帮助别人和思考超前的学习内容（比如，如何用代数天平秤来展示代数等式）。这节课还体现了教学的多元化，爱德华老师不仅用讲授和展示的方法，还用提问、小组讨论、学生表达和展示的方法，极大地提高了学生的参与度。

（6）评价性：爱德华老师在講授新课之前，通过POD就已教内容对全班学生做了检测。这个检测活动是有目的的，并且是随课堂教学而进行的，比如，他让学生与相邻同学相互阐述等式的内容和日常生活的例子，然后由学生代表在全班进行阐述；再比如，他让学生与相邻同学讨论并将他们创造的含有一个未知数的方程式在全班与其他同学分享。结束时，他让学生用日志来反映学习的情况。这些例子说明，爱德华老师用不同的方法了解学生掌握新知识的程度，以帮助他自己实时调整讲课的内容。

（7）创新性：爱德华老师使用代数天平秤来阐述代数等式的特点：开放等式和两边相等显得有新意。特别是对负数在等式中的应用，利用带有负数的代数天平秤来阐述十分直观，起到了帮助学生从直观思维到抽象思维过渡的目的。爱德华老师并不是一味地按照教科书的顺序来教学，而是按照学生的理解程度来设计教学进度，以使教学材料有新意，有吸引力，使得学生在探究中学习。

（8）互动性：爱德华老师不仅鼓励学生与其他同学讨论问题，给学生创造互动的机会，而且还自己投入到学生中与学生互动。本节课，学生共有数次的互动机会，增强了团队的意识。老师通过与学生的互动，了解了学生，特别是学习能力低的学生对数学概念的理解程度，从而促进学生自发参与学习。

（9）反思性：爱德华老师在课中有意识地引导学生互相讨论、自我指导、自我反思、自我评价。在课结束时，学生有机会用数学日志的方式来反思所学的内容。他还用抽卡片的随机方法来鼓励学生的参与而不是按照学生成绩的好坏来让学生回答问题，这既体现了公平又使得学生随时都要集中注意力。

（10）公平性：这个班虽然有不同程度的学生，但爱德华老师竭尽全力建立公平的学习环境，尊重不同智力孩子的努力，使课堂具有宽容的学习气氛。比如，用不同的教学手段（运用教学用具来帮助不同程度的学生）；用不同的数学表达（语言表达、数学式子表达、实际问题表达、方框图表达以及书面写作表达）来展示学生对数学概念的理解；用不同的方法（老师授课、学生小组讨论、老师随机抽查学生）来鼓励学生的参与。

（11）责任感：此课体现爱德华老师具有较高的课堂管理艺术。学生具有较强的组织纪律性和责任感。他们知道来到此课堂的目的是学习而不是其他。学生们与他人讨论，有助于培养学生的小组合作精神，无论学习好坏，都把自己看作是小组的一员。同时也帮助学生树立让每个人都成为学习中的胜利者的非常积极的人生态度。

（12）有效性：这节课基本上没有浪费时间。全课用了56分钟（93%）在教学内容上。由于学生的投入和参与，全课基本上没有纪律问题。

说明：本节课是作者在课堂教学研究中的课例之一，系作者亲自观察得到。为了了解学生的学习情况，课后作者将印有两个小问题的小纸条交由学生填写作为学习反馈。这两个小问题是让学生创造性地陈述他们从这堂课所学到的知识并给出一个实际例子来说明他们对所学知识的应用。结果表明大多数学生达到了本课的教学要求。