基于TOPSIS和BPNN的网球运动员“势头”的量化研究

一、简介

当今社会，网球这项体育运动越来越受欢迎。频繁的赛季转换、高密度的比赛安排和以赛代练是网球的显著特点[1]，当描述比赛的整体走势出现了不可思议的波动或者转折点时，“势头”这个词被经常提及。“势头”指运动员在一系列事件之后获得的一种能够提升比赛状态和气势的动力，它在网球比赛的走势中起到了相当重要的作用。[2]

在2023年温布尔登网球公开赛男子单打决赛中，尽管阿尔卡拉斯在第一盘中落后了5分，他在第二、三、五盘中分别以7-6， 6-1， 6-4比分获胜，最终逆转局势，打败了德约科维奇。于是，一个自然的想法是，在这场比赛中“势头”在阿尔卡拉斯第一盘大幅度落后及后面乘胜追击时发挥作用，扭转了比赛结果。根据以上背景，本文将“势头”选做研究对象。但考虑到“势头”是一种球员在比赛过程中拥有动力的主观感受，很难进行准确的刻画，无法衡量球员在某一时刻有多少“势头”，也难以说明“势头”在一场比赛中是如何产生及变化的。

基于此，本文的主要任务是给“势头”一个量化的指标，找到在“势头”不断作用下比赛局势发生逆转的具体时刻，同时找出对“势头”影响较大的因素。本文利用2023年温布尔登网球公开赛男子单打比赛的数据进行研究，并考虑了如下假设：

1.两个球员综合实力的差距可以用他们在ATP上的实时排名的差距来衡量。

2.环境等客观因素如天气、场地等不影响球员的表现水平。这是因为比赛会因不理想的天气延后，并且承办比赛的场地均满足一定的标准。

3.比赛轮次不影响球员的状态。即每个球员的比赛状态在不同场、盘及局中保持稳定。

4.每一分的比赛结果只影响球员下一分比赛中的表现水平，且每一分在比赛进程中的位置不影响球员的状态。由于比赛的盘数和比分在一定程度上能够体现比赛的进程，于是本文假定在局点和盘点时的关键分与非关键分对球员的影响是一样的。

5.每一得分的性质相同。由于双发失误、ACE球、破发点等具有特殊性质的分已经在比赛结果比分中有所反映，故此处不加以考虑。

二、数据集介绍及预处理

2023年温布尔登网球公开赛男子单打比赛决赛的数据包含了31场比赛中每一分的信息。每一行数据含有比赛编号、盘数、局数、分、球员双方的名称等基本信息。本文将此数据集中的每行分别以两个球员作为主体，拆分为两行，将数据集整理成共含有了14568行的新数据集。则新数据集的各行拥有唯一主体，称为球员，同一分中的另一方被称为对手。

数据集中与比赛表现相关的变量符号及含义如表1、表2、表3所示。

此外，本文还定义了两个组合变量：Server_count×Server，Server×Speed_no，分别记为Server_no，Speed。根据假设5，P1_ace，P1_break等变量含有的特殊信息已蕴含在比分中，故不需要添加额外变量。

本文利用随机森林填补了speed_no中含有的752个缺失值。经过检验，未发现不符合常识的离群值，故不进行其他处理。

三、“势头”的衡量及比赛结果的估计

（一）基于TOPSIS熵权法的“势头”的量化估计

考虑到“势头”是一种比赛状态，本文利用与比赛表现相关的变量来估计球员在比赛指定时刻的“势头”的多少。

根据假设3与4，每一分所处位置不影响球员状态，故本文能够把每一分的信息作为被评价对象，并利用TOPSIS熵权法给出一个比赛状态评分。评分越高说明球员在这一分的“势头”越大，表现得越好，赢的可能性也越大。此评分就是“势头”的一个量化指标。

1.熵权法为指标赋权

指标权重的确定是TOPSIS的重要环节，而采用熵权法可有效消除主观判断的影响。它利用熵值判断指标的离散程度，并把熵值更大的指标赋予更高的权重。接下来采用此方法计算权重。

共有14568个被评价的分，24个评价指标。首先构建判断矩阵：X=（xij）14568*24（i=1，2，…，14568;j=1，2，…，24）。对判断矩阵进行标准化处理，得到

xij'=xijxjmax

其中xjmax指第j个指标的最大值。接下来计算信息熵

Hj=-k∑14568i=1pijlnpij，j=1，2，…，24

其中pij=xij'∑14568i=1xij' ，k=1ln14568。进一步得到第j个指标的权重

ωj=1-Hj∑24j=11-Hj

其中ωj∈［0，1］，且 ∑24j=1ωj=1。指标权重计算结果如表4所示。

最后，计算出加权矩阵

R=（rij）14568×24

其中rij=ωj*xij'（i=1，2，…，14568;j=1，2，…，24）。

2.基于TOPSIS的“势头”的量化估计

首先将指标转化成数值越大越好的极大型数据，并进行标准化。

接下来使用TOPSIS对球员的比赛状态进行评价。首先确定各指标的最优理想解A+和最劣理想解A-。由于所有指标均已转化为极大型数据，所以各指标中最大值代表最优情况，最小值代表最劣情况，即

A+j=max（r1j，r1j，…，r14568j），A-j=min（r1j，r1j，…，r14568j）

然后计算每个球到A+与A-的距离

D+i=∑24j=1（A+j-rij）2，

D-i=∑24j=1（A-j-rij）2

进一步能够计算出球员在第i分时刻的比赛状态评分

Ci=D-iD+i+D-i，Ci∈［0，1］

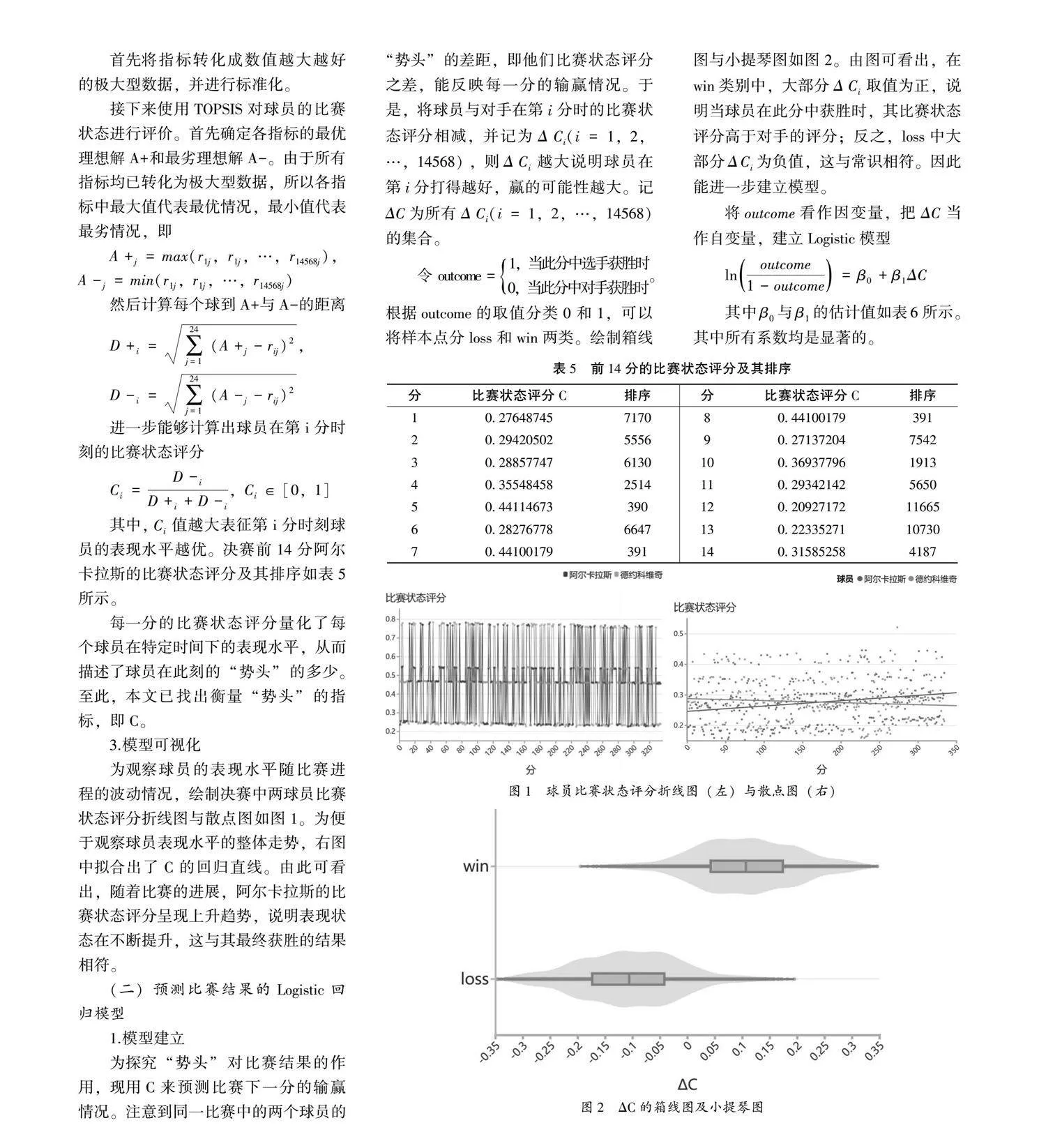
其中，Ci值越大表征第i分时刻球员的表现水平越优。决赛前14分阿尔卡拉斯的比赛状态评分及其排序如表5所示。

每一分的比赛状态评分量化了每个球员在特定时间下的表现水平，从而描述了球员在此刻的“势头”的多少。至此，本文已找出衡量“势头”的指标，即C。

3.模型可视化

为观察球员的表现水平随比赛进程的波动情况，绘制决赛中两球员比赛状态评分折线图与散点图如图1。为便于观察球员表现水平的整体走势，右图中拟合出了C的回归直线。由此可看出，随着比赛的进展，阿尔卡拉斯的比赛状态评分呈现上升趋势，说明表现状态在不断提升，这与其最终获胜的结果相符。

（二）预测比赛结果的Logistic回归模型

1.模型建立

为探究“势头”对比赛结果的作用，现用C来预测比赛下一分的输赢情况。注意到同一比赛中的两个球员的“势头”的差距，即他们比赛状态评分之差，能反映每一分的输赢情况。于是，将球员与对手在第i分时的比赛状态评分相减，并记为ΔCi（i=1，2，…，14568），则ΔCi越大说明球员在第i分打得越好，赢的可能性越大。记ΔC为所有ΔCi（i=1，2，…，14568）的集合。

令outcome=1，当此分中选手获胜时0，当此分中对手获胜时。根据outcome的取值分类0和1，可以将样本点分loss和win两类。绘制箱线图与小提琴图如图2。由图可看出，在win类别中，大部分ΔCi取值为正，说明当球员在此分中获胜时，其比赛状态评分高于对手的评分；反之，loss中大部分ΔCi为负值，这与常识相符。因此能进一步建立模型。

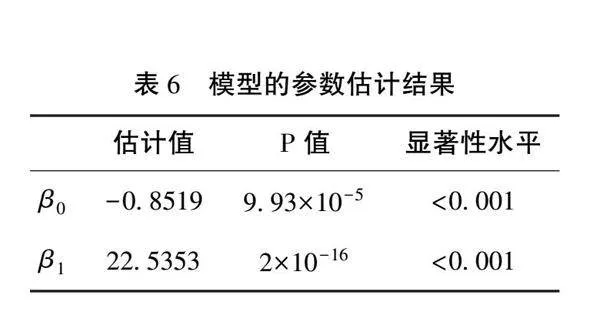
将outcome看作因变量，把ΔC当作自变量，建立Logistic模型

lnoutcome1-outcome=β0+β1ΔC

其中β0与β1的估计值如表6所示。其中所有系数均是显著的。

2.10折交叉验证

为评估模型的预测效果，现进行10折交叉验证。首先将样本集随机地划分为样本量相同的10部分[3]，把前9部分当作训练集，用于建立模型及拟合参数；最后1部分当作测试集，以此来估计平均预测准确率。

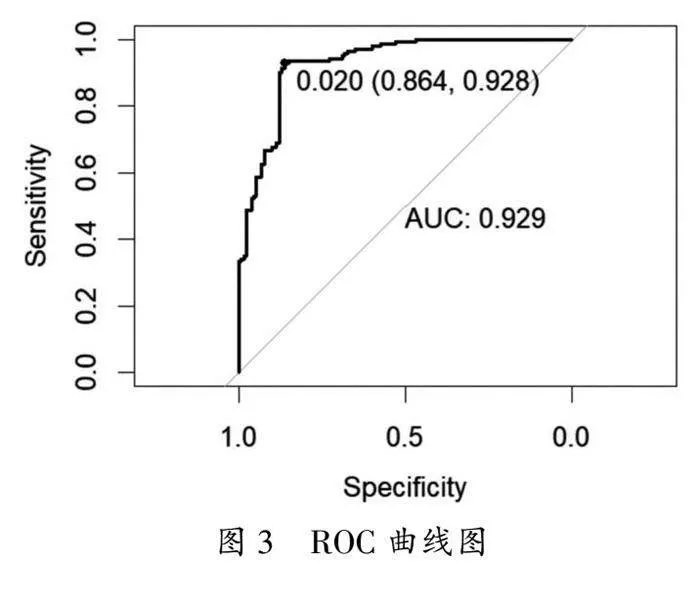
其次，绘制ROC曲线如图3所示，由图可得到用于判断预测类别的最优阈值=0.020。于是，对于测试集的样本点，如果它的后验概率≥0.020，则此点的outcome被判为1；否则，outcome被判为0。将预测得到的outcome与测试集中outcome的真实值进行比较，计算得到预测准确率为0.8333。

此外，计算得到AUC为0.929，非常接近1，说明此模型有很强的二元分类能力，区分两个类别的表现很好，且ROC曲线是可靠的[4]。

最后将上述操作重复200次，计算得到平均预测准确率为87.9%，说明模型比较稳健且预测效果不错。

四、转折点的识别与“势头”的刻画因素

（一）基于核回归方法的转折点识别

前文已说明“势头”会对比赛结果造成影响，接下来的目的是描述“势头”如何在比赛中发挥作用。具体来说，希望找到在“势头”不断作用下，比赛走势从有利于某一方转化为另一方的具体时刻，即比赛的“转折点”。

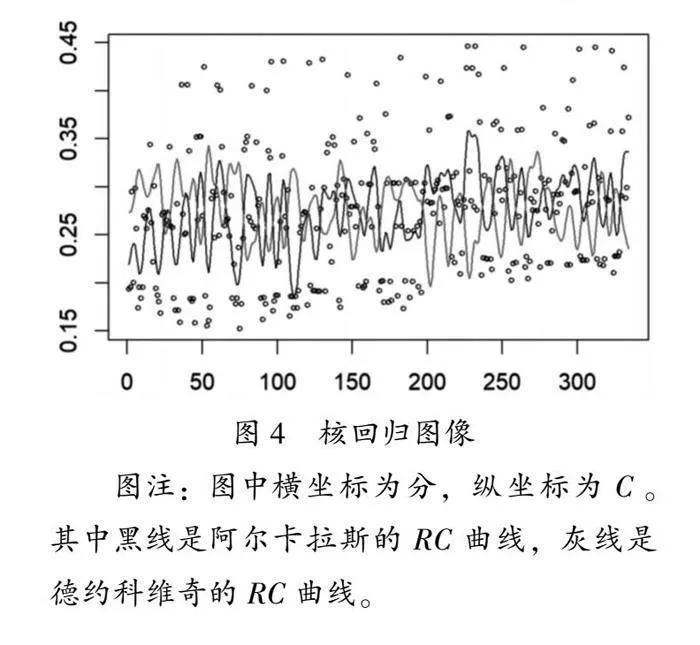
从直观上来看，当一方选手的表现得更好时，比赛走势更有利于这一方。故首先考虑用球员比赛状态评分的差值当作自变量。但由图1右图可以看出，C变化特别大且迅速，故直接使用ΔC作为自变量难以识别出ΔC正负号的变化规律。因此接下来对C进行核回归，使得ΔC的变化更加平滑，便于识别转折点的发生。

本文把C当作因变量，把分当作自变量，进行核回归拟合，记拟合后的比赛状态评分为RC，并绘制同一场比赛双方的核回归曲线如图4所示。两条曲线的交点就是转折点发生的时刻，距离转折点最近的分就是“势头”扭转比赛局势的那一分。为简化表达，本文把上述距离转折时刻最近的分简称为转折点。

（二）基于BPNN的自变量重要性的评估

为了找到对“势头”影响较大的指标，并计算出每个指标影响的大小，本文采用BPNN。此算法具有大规模并行结构、分布式存储等特点[5]，有很强的分类能力。

为充分利用在转折点出现之前的ΔRC随比赛进程不断减小的信息，本文把转折点与其前两个点一起看作“转折时刻”。定义出用于判断点是否位于转折时刻的指标

reversion =1，此点位于转折时刻

且ΔRC由负转正0，此

点不位于转折时刻

-1，此点位于转折时

刻且ΔRC由正转负

为了探究哪些因素影响转折时刻，现把reversion当做因变量，使用reversion=1或-1的点对应的数据，把各项指标当做自变量，使用BPNN对reversion的分类进行预测。计算得到预测准确率为75.9%。

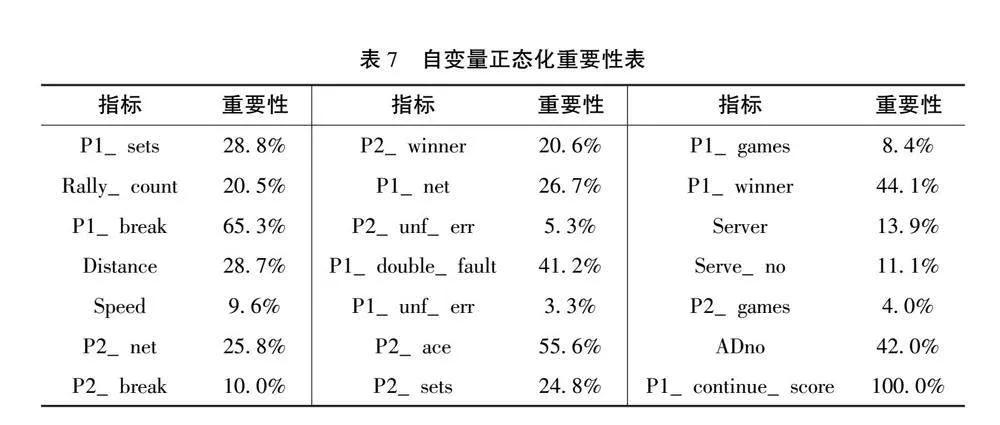
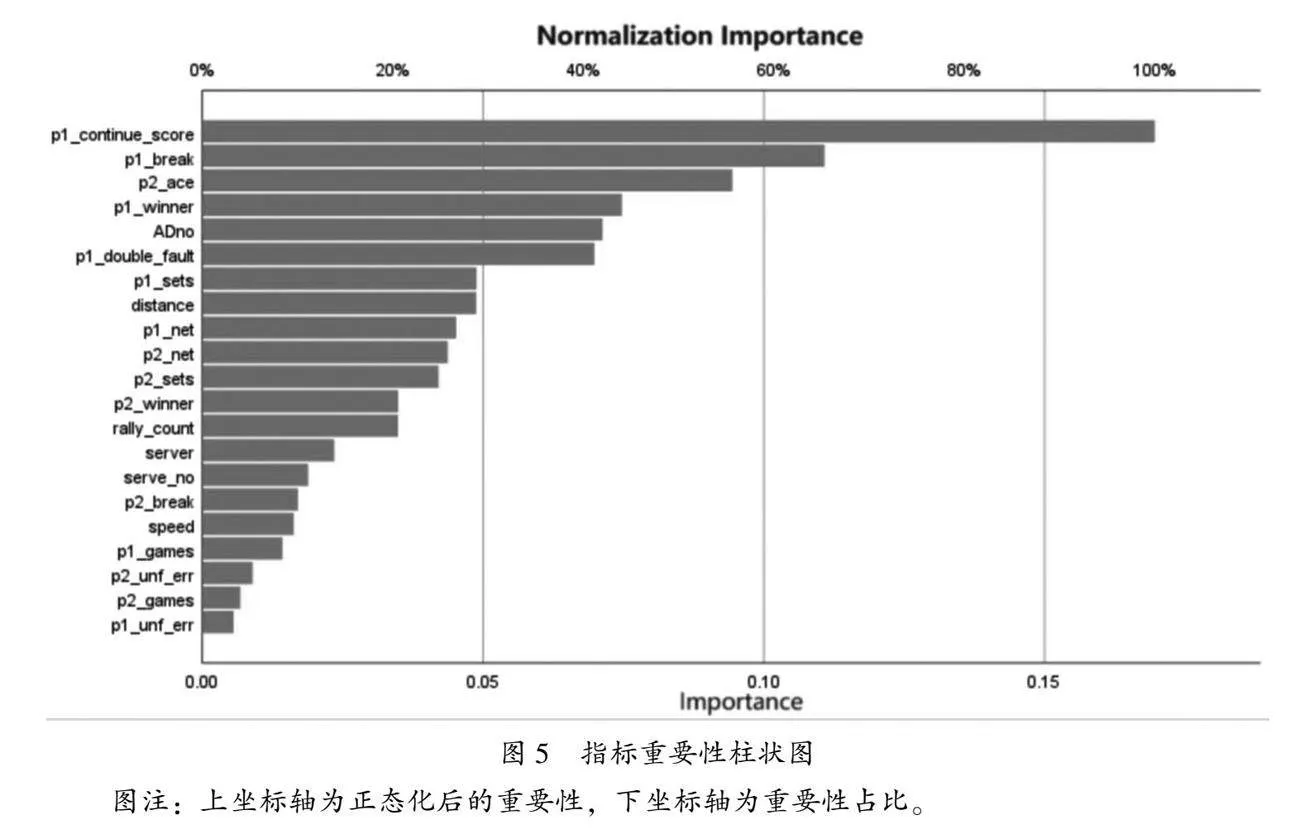
在进行BPNN 时，训练集的样本点被分为几个批次，每个批次依次进行训练。而权重更新就是在两个训练批次切换之间进行的。[6]这些权重可以被理解为每个指标解释了多少因变量的变化，即每个指标对转折时刻的影响有多大。于是，指标的权重就是其重要性的一种量化。经过正态化的自变量重要性如表7所示。此外，为便于直观地观察自变量重要性的排序，绘制柱状图如图5。

从图5可以看出，重要性最高的自变量是P1_continue_score，即球员连续得分与失分次数，占比达到17%。研究表明每局比赛中“连续得两分”和“连续失两分”是技战术变化的关键时机[7]，此处从运动员“势头”的角度来验证了此结论。当选手在比赛中连续得分时次数越多时，他获胜的概率越大。这是因为连续得分能够使球员更加有斗志，即增加了“势头”，从而他获胜的可能性也越高。因此，在运动员日常比赛中，应更加关注此因素，在球员连续得分时把握“势头”，一鼓作气；在连续失分时及时调整状态，恢复动力。

重要性占比第二的变量是球员在破发点的情况，占比为11%。相关文献说明高水平球员在破发点关键分上的获胜率高于其他分数，即高水平球员在比赛的重要时刻能够表现出更好的状态，且这种能力具有相对的稳定性[8]。于是，在关键时刻以良好的状态面对压力，把握住每个破发点，能够为球员增加“势头”，提升获胜概率。

对手打出ACE球的次数是重要性排名第三的变量，占比9%。当对手打出ACE球的次数增加时，球员的“势头”也会发生较大改变，从而影响了比赛结果。这为球员的训练提供了两点建议：第一，提高接发球的能力，降低比赛中对手打出ACE球的频率，能够减少“势头”的衰减；第二，锻炼球员在对手打出ACE球之后的状态调节能力，尽量保持“势头”的稳定，尝试发挥其积极作用，从而扭转比赛的不利走势。

五、结论

1.任意时刻的运动员“势头”的多少能够用比赛状态评分C衡量，C∈［0，1］，且C越高说明此分中球员的表现越好。

2.在网球选手及赛况的研究中，过去的理论将比赛中的球员每一分的表现看作是相互独立的，但现在越来越多研究表明，过去比赛的分数、表现等因素都会影响球员接下来的比赛状态。[9]“势头”为球员提供激励与动力，影响了比赛每一分的结果。可通过如下模型预测任意分的比赛结果outcome。

lnoutcome1-outcome=-0.8519+22.5353ΔC

其中ΔC是球员与对手C的差值。此模型的平均预测准确率为87.9%。

3.“势头”在比赛中发挥作用的具体时刻体现在转折点上。两个球员核回归拟合后的比赛状态评分曲线的交点就是转折点发生的时刻。通过BPNN对转折时刻的预测准确率为75.9%。

4.对“势头”影响最大的三个因素为：选手连续得分或者失分的次数、球员在破发点的情况及对手打出ACE球的次数，重要性占比分别为17%，11%和9%。在日常训练及比赛中重视上述因素，并及时调整球员的心态和身体状态，能够有效发挥“势头”的积极作用，提升比赛获胜的概率。

参考文献：

[1]时广彬，任杨千千，石磊，等.基于机器学习的网球最佳回球落点决策模型[J].体育科学，2023，43（06）：53-60.

[2]Klaassen and Magnus （2014）.Analyzing Wimbledon. The Power of Statistics， Oxford University Press.

[3]Gareth James， Daniela Witten， Trevor Hastie， Robert Tibshirani. An Introduction to Statistical Learning with Applications in R. Springer; 2021. p. 203-205.

[4]Roumeliotis， S.，Schurgers，J.，Tsalikakis，D.G.et al. ROC curve analysis： a useful statistic multi-tool in the research of nephrology. IntUrolNephrol （2024）. https：//doi.org/10.1007/s11255-024-04022-8.

[5]TuJuanjuan. Research on Learning Algorithm of Neural Nerwork Optimized with PSO and its Application[D]. Jiangsu University， 2013.

[6]韩普，周汉辰，周北望.BP神经网络原理研究与实现[J].广播电视信息，2018，0（10）：121-125.

[7]刘明朋，刘晨.世界优秀女子网球运动员连续得失分特征研究[J].Sports World，2019，（05）：23-24.

[8]GONZALEZ-DIAZ J，GOSSNER O，ROGERS BW， 2012. Performing Best When It Matters Most ： Evidence From Professional Tennis [J].J Econ Behav Organ， 84（3）：767-781.

[9]Jackson， D. and Mosurski， K. （1997）. Heavy Defeats in Tennis：Psychological Momentum of Random Effect. Chance， 10：27-34.Dqsad.

责任编辑 朱守锂