离散数学课程思政教学设计与实践

摘" 要：课程思政是落实立德树人根本任务的关键举措。作为计算机类专业基础课程，离散数学在专业课程体系中具有重要的作用，在课程教学中推进课程思政建设是极为必要的。该文根据离散数学教学的素养目标，从该课程教学体系设计、课程思政融入点及实现方式方面具体介绍线上线下相结合的课程思政实践过程，充分发挥课程育人的主渠道作用，为培养德才兼备的专业技术人才奠定基础，也对其他专业课程教学中融入思政教育提供参考。

关键词：课程思政;离散数学;教学设计;线上线下;思政元素

中图分类号：G642" " " 文献标志码：A" " " " " 文章编号：2096-000X（2025）05-0173-04

Abstract： Curriculum ideological and political education is a key measure to implement the fundamental task of cultivating morality and cultivating talents. As a fundamental course in computer science， Discrete Mathematics plays an important role in the professional curriculum system， and it is extremely necessary to promote the ideological and political construction of courses in curriculum teaching. Based on the teaching goals of Discrete Mathematics， this paper introduces the online and offline mixed teaching practice process for political education of Discrete Mathematics from the design of the teaching system， the integration points of ideological and political education in the course， and the implementation methods. It lays the foundation for cultivating professional and technical talents with both moral and talent， and providing reference for integrating ideological and political education into other professional curriculum teaching.

Keywords： curriculum ideological and political education; Discrete Mathematics; teaching design; online and offline mixed teaching; weighted graph; ideological and political element

2016年12月，习近平总书记在全国高校思想政治工作会议上指出“要坚持把立德树人作为中心环节，把思想政治工作贯穿教育教学全过程，实现全程育人、全方位育人”[1]。2020年5月，教育部印发了《高等学校课程思政建设指导纲要》，强调把思想政治教育贯穿人才培养体系，全面推进高校课程思政建设，发挥好每门课程的育人作用[2]。为深入贯彻落实习近平总书记关于思政课建设的重要论述、关于“大思政课”的重要指示和在中国人民大学考察时的重要讲话精神，全面推动思政课改革创新，推动思想政治教育创新发展，教育部等十部门2022年印发了《全面推进“大思政课”建设的工作方案》[3]。

离散数学是研究离散量的结构及其相互关系的数学学科，它在各学科领域，特别在计算机科学与技术领域有着广泛的应用。作为计算机类专业的重要专业基础课程，离散数学也是计算机科学的许多专业课程，如程序设计语言、数据结构、操作系统、编译原理、人工智能、数据库和算法设计与分析等必不可少的先行课程[4-5]。如何在离散数学课程教学中推进课程思政建设，提高本课程与思政教学的融合度，做到知识传授与价值引领的有效结合，是授课教师应该认真思考和探索的问题。

一" 离散数学课程目标

通过离散数学的学习，不但可以掌握处理离散结构的描述工具和方法，为后续课程的学习创造条件，而且离散数学所提供的训练可以帮助学生提高抽象思维能力和逻辑推理能力[6]，有益于学生严谨、完整、规范的科学态度的培养，为其将来参与创新性的研究和开发工作打下坚实的基础。本课程的具体目标如下。

知识目标：理解并掌握命题逻辑、谓词逻辑、二元关系、集合论、图论和关系代数等基本概念、基本理论及其内在联系，能够利用离散数学的概念、理论与方法分析表达复杂工程问题。

能力目标： 通过课前、课后学习，培养学生自主学习的能力;通过课堂讨论，培养学生团队协作、沟通交流的能力。掌握以关系、群、环、域和图等可以建立的数学重要模型，综合运用基本知识和技能，识别复杂工程问题的关键环节和参数，表达并解决复杂工程问题;通过数学素养的培养和思维方式的锻炼，提升严谨缜密的数学思维能力，提高面向计算机复杂工程问题的抽象思维、概括分析、逻辑推理的能力。

素养目标：了解离散数学对计算机各个方向的科学意义，了解离散数学重要数学模型和方法的发展历程，树立坚定的科学信念，形成科学的世界观、人生观和价值观，树立坚定理想信念，激发爱国情感，增强社会责任感和使命感;培养学生的批判性思维和对新知识的探索精神;将中国传统文化元素与知识点紧密融合，坚定文化自信。

二" 课程思政教学体系设计

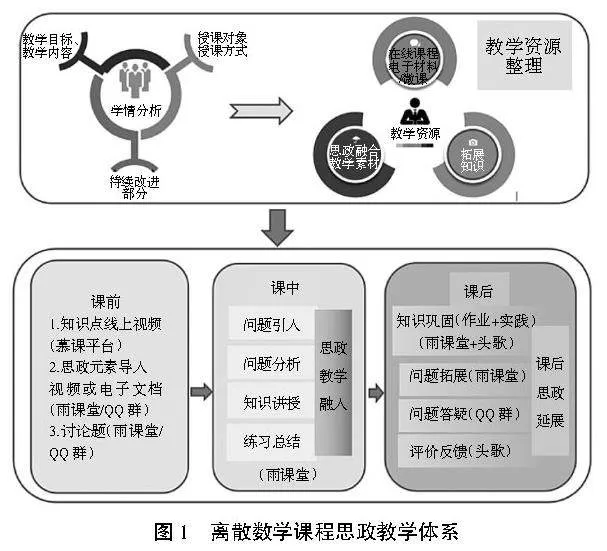
作为一门专业核心课程，离散数学课程思政和专业知识的融合要做到润物细无声，潜移默化地将价值观的元素植入专业知识授课和实践中。本课程的课程思政教学体系如图1所示。

在课程教学开始之前，课程组首先分析学院计算机类三个专业学生对该课程的掌握和需求情况，为该课程教学体系和教学内容的修改提供科学依据。具体实施中，结合教学开展方式，进一步分析课程目标以及前一学年该课程的学生达成度分析报告，对该课程的教学内容进行设计。在此基础上，课程组对该课程的教学资源，如知识点短视频、电子材料、相关思政素材（文档或视频等）进行补充整理。根据专业培养目标的要求，结合教学大纲，对离散数学教学内容进行统一梳理，针对离散数学四个部分的知识点，不断挖掘思想政治元素，寻找思想政治教育与离散数学的结合点，建立每个知识点和各个思政元素的联系，构成课程的思政地图。例如，讲授图论起源时，可以介绍相关科学家对待科学问题的态度和精神，培养学生对新知识的探索精神和独立思考的意识。讲解最短路径时，可以引入“一带一路”天然气管道铺设、中国邮递员问题等，树立民族自豪感和自信。通过不断优化和整合课程教学内容，逐步规范课程教学设计方案，使专业课与思想政治理论课紧密结合，形成同向同行的育人格局。

离散数学课程思政教学过程采用线下线上相结合的方式，包括课前、课中和课后3个阶段。课前，课程组老师基于雨课堂和学堂在线线上课程资源，在线发布下次课需要讲授知识点的相关预习任务，主要包括预习课本知识、查阅相关知识应用或调研相关知识历史背景等。课程组根据课程具体内容提前提炼出与课程内容相关的思政元素，让学生在调研学习知识点相关材料的时候，产生对所授知识的兴趣，同时对国家政策方针、数学知识的发展、中国文化等有更进一步的了解，厚植爱国情怀，坚定民族自豪感和文化自信，树立勇于探索科学知识的信念。

课堂教学主要在线下进行，包括问题引入、问题分析、知识讲授、课堂练习总结。在线下各教学环节中，基于知识点，植入课前挖掘好的思政元素。教师要引导学生针对课前预习内容进行交流，让学生体会到深层次的思政内容。在知识讲授完，通过雨课堂在线答题的方式，考核学生对知识点的掌握情况。

课后主要包括布置课后作业，离散数学课后作业主要基于雨课堂和头歌两个平台开展。在雨课堂中，课程组布置针对知识点的客观和主观题;在头歌平台布置相关编程实践题;“理论+实践”相结合的作业模式进一步巩固学生对知识点的掌握。课程组将思政教育进一步延伸至课后，通过对知识点所涉及的思政元素进一步拓展，以实际问题、案例的方式让学生去阅读、思考。

三" 课程思政融入点及实现方式

本课程采用线上线下混合式教学模式，课程贯彻OBE理念，基于知识目标、能力目标和素质目标反向设计了混合式课堂的教学内容，并在实践中不断改进。在素养目标培养方面，本课程主要通过以下途径开展思政教育。

（一）" 修订课程大纲，体现思政目标

在离散数学教学同课程思政有机融合的过程中，首先要重新修订教学大纲，明确把开展课程思政建设加进离散数学教学任务。在课程教学内容中要增加政治信仰、社会责任、文化自信等教育内容。最终要实现价值塑造、能力培养、知识传授三位一体的课程目标，并且把思政目标和毕业要求的指标结合起来。

（二）" 挖掘离散数学蕴含的思政元素，构建思政地图

在保证课程教学内容总体不变，知识技能目标有效达成的前提下，根据离散数学课程的特点，坚持正确的育人导向，在教学设计中充分挖掘课程知识点相关的思想政治元素并将其有机融入课堂教学环节中，以实现思想政治的育人目标。主要通过两个方面去挖掘思政元素。

1" 数学发展史

离散数学课程中逻辑、集合与关系、图论、代数系统四个部分都蕴含着丰富的数学史。在讲解这四个部分的理论知识时，可以将定义、公式、定理以及算法的起源、发展和相关数学家的生平逸事介绍给学生，如德摩根的坚韧正直、欧拉的勤奋执着等[7]。培养学生勇攀科学高峰、迎难而上，敢于同困难做斗争，勇于创新的精神，同时激发培养学生勇攀科学高峰、迎难而上，敢于同困难做斗争，勇于创新的精神，同时激发爱国爱党，为国家富强永攀科学高峰的信念和意志，引导其树立正确的世界观、人生观和价值观。

2" 与社会、生活相关的应用案例

离散数学理论性强，抽象性强，学生往往感觉该课程难学难懂，提不起学习兴趣。在教学过程中利用社会生活中的案例作为知识点引入，技能提高学生的学习兴趣，引导学生去分析、思考问题，也能通过这些案例让学生对时政方针、祖国文化等有进一步理解，培养学生理论联系实际的作风的同时树立民族自豪感和文化自信。这部分内容中引入中国邮递员问题、项目管理问题、网络布局问题、航空调度和航班的设定、城市的交通管理、奇偶校验图灵机等实例，调动学生的积极性，培养学生的工程思维和创新意识，严谨细致的工作作风[8]。

介绍离散数学对软件和信息技术发展的重要作用，引入我国科技发展中“卡脖子”技术问题。提升学生在逆境中创新发展、锐意进取、坚守职业、勇于挑战、无私奉献和勇攀高峰的科学探究精神。培养学生科研报国的责任感、使命感和求真务实的科学精神。

（三）" 在混合式教学过程中有效融入思政元素

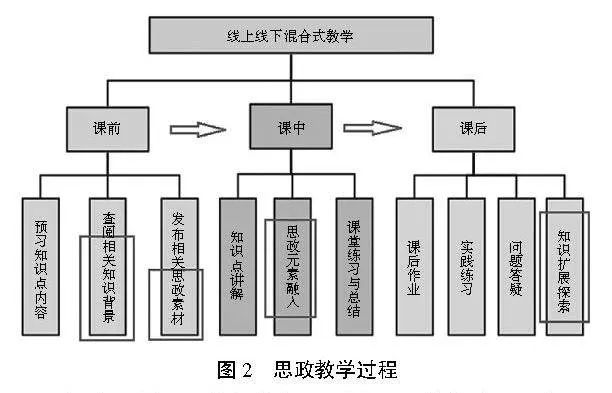
教学团队建设了在线课程，采用了线上线下的混合式课堂教学。通过课前思政素材学习发布，课中将思政元素作为知识点引入、案例分析，课后将思政元素以问题调研分析的方式将思政教育贯穿到整个课程教学过程中，如图2所示。在课堂上，针对具体问题，通过组织学生开展研讨，也培养了学生的沟通交流能力。

例如，我们在讲授带权图的定义、最短路径问题这些知识点时，首先在课前通过线上平台发布了一些课程材料，如“一带一路”倡议、导游规划旅游线路问题、结构程序设计之父Dijkstra生平等。在上课时，以互动交流的方式介绍丝绸之路和“一带一路”倡议，让学生认识理解自己祖国在推动全球共赢、和平发展所体现出来的负责任、大国的气度和胸襟。“一带一路”是中国与丝路沿途国家分享优质产能，共商项目投资、共建基础设施、共享合作成果，内容包括道路联通、贸易畅通等。在讨论中同时抛出一些问题让学生思考，比如铺设两个国家之间的天然气输送管道，如何铺设才能达到管道互通并用料最少呢？对于沿线两个城市之间的航行，如何规划使得从城市A到城市B的飞行时间最短？该如何对这些问题建模后求解呢？

进而引出带权图的概念。在计算机网络建模中，通信成本、计算机在这些线路上的响应时间或计算机之间的距离等都可以用加权图来研究[9-10]。在此基础上，以一个旅游城市导游规划旅游线路问题为例，引入最短路径问题，同时借旅游城市悠久的历史介绍来进一步树立文化自信。

在此基础上，我们对最短路进行数学建模，给出形式化的描述。进而引导学生思考，带权图建模后，该如何求出图中两个结点间的最短路径？进一步地引出求解最短路径的Dijkstra算法。在具体讲授Dijkstra算法之前，课程教师会对Dijkstra所作出的贡献做一个简单介绍。介绍Dijkstra在人生不如意的时期（对计算机学科存在偏见的时代）仍然积极投入工作、持之以恒从而创造经典。鼓励学生努力学习、刻苦钻研专业知识。同时借Dijkstra敏锐的洞察力，敢于质疑恩师Van Wijingaarden的ALGOL 68语言，鼓励学生发挥独立思考的能力，培养批判性思维。

四" 结束语

本课程教学过程中，课程组教师积极进行“知识传授与价值引领相结合”的课程思政教学改革及探索，实现“立德树人、润物无声”。融入思政元素的离散数学课堂悄悄地发生了改变：教学内容更丰富，理论与实际联系更紧密，师生关系更融洽。思政元素的引入，增强了教学过程的互动性和生动性，激发学生之间的知识共享与价值认同，激发学生学习热情和学习动力。师生之间不但有知识、技术层面的交流，还多了思想层面的交流。一旦思想层面产生共鸣，师生的关系就更亲密，专业学习更愉快，培养目标的完成更顺利。

近年来，离散数学课程高质量地完成了教学任务，课前、课中、课后三个阶段相互衔接，相互配合，确保知识、能力、素质目标有效达成，也深受学生的好评。本课程先后在学校课程思政教学设计案例大赛、示范性课程建设方面获得立项支持和奖励。

参考文献：

[1] 习近平：把思想政治工作贯穿教育教学全过程 开创我国高等教育事业发展新局面[N].人民日报，2016-12-09（01）.

[2] 贾经冬，李卫国.离散数学课程思政教学设计与实践[J].计算机教育，2022（3）：102-105.

[3] 教育部等十部门关于印发《全面推进“大思政课”建设的工作方案》的通知[J].中华人民共和国教育部公报，2022（10）：8-14.

[4] 邵婷婷，邵珠艳，古鲁峰.离散数学的课程思政建设与实践[J].计算机教育，2021（11）：115-119.

[5] 邹乐，王晓峰，吴志泽，等.课程思政视域下计算机专业基础课的教学研究——以“离散数学”为例[J].合肥学院学报（综合版），2021，38（2）：140-144.

[6] 刘亚婷，尚顺先.课程思政背景下“离散数学”教学模式改革[J].教育教学论坛，2021（39）：96-99.

[7] 王磊，仇海全，李焱.课程思政视域下离散数学课程的教学改革实践探究[J].电脑知识与技术术，2023，19（10）：154-156，165.

[8] 何楚明，刘冬宁.离散数学课程中计算思维与课程思政的切入与融合[J].计算机教育，2023（2）：79-82.

[9] 贾保敏，孔维宾.离散数学教学的课程思政探析[J].软件导刊，2022，21（2）：221-225.

[10] 公徐路.课程思政下离散数学课堂教学中的改革与实践[J].大学数学，2020，36（4）：25-30.

基金项目：教育部产学合作协同育人项目“新工科大数据与信息安全专业师资培训”（220606008072028）;河南省高等教育教学研究项目“面向专业胜任力的计算机复合创新型人才培养体系研究与实践”（2021SXHLX043）;河南省新工科研究与实践项目“新工科背景下计算机科学与技术创新实践能力培养模式探究”（2020JGLX011）;河南大学首批本科专业核心课程提质建设项目“离散数学课程”（HDTZJS2023-037）;2023年度河南大学研究生教育教学改革研究与实践项目“双一流背景下的生物信息学研究型创新人才培养模式探索与实践”（YJSJG2023XJ068）;河南大学本科教学改革研究与实践项目“基于BLOOM+OBE的计算机类创新性研究型人才培养课程群建设”（HDXJJG2022-040）;河南大学研究生培养创新与质量提升行动计划项目“《专业英语》课程思政示范课程”（SYLKC2022006）

第一作者简介：阎朝坤（1978-），男，汉族，河南开封人，博士，教授。研究方向为人工智能。

*通信作者：罗慧敏（1980-），女，汉族，河南周口人，博士，副教授。研究方向为生物信息学。