常微分方程核心课程教学改革

2025-02-13陈爱敏

高教学刊 2025年5期

摘" 要：常微分方程课程是数学类专业基础课中的一门核心课程，也是数学分析、高等代数和解析几何的后继课程。在学生构建专业的数学理论体系过程中具有非常重要的作用。该文基于河南大学数学与统计学院分设的四个专业各自的不同特点，从课程教学目标、教学方法与学生学习能力提升等方面提出关于常微分方程课程分类、分层等教学模式改革，充分发挥教学团队的优势，借助在线教学平台，最大可能实现以学生为主体的教学模式，构建新的评价体系，在合适的节点融入思政元素，加强课程思政引领。力争通过改革实现更加适应当今教育理念和更加符合学生时代特征的教学模式。

关键词：常微分方程;核心课程;分类教学;分层教学;团队教学

中图分类号：G642" " " 文献标志码：A" " " " " 文章编号：2096-000X（2025）05-0128-04

Abstract： The course Ordinary Differential Equations is a core course in the basic courses of mathematics majors， and it is also a successor course to Mathematical Analysis， Advanced Algebra， and Analytical Geometry. It plays a very important role in the process of students building a professional mathematical theoretical system. This paper based on the different characteristics of the four majors set up by the School of Mathematics and Statistics of Henan University. From the aspects of course teaching objectives， teaching methods， and students' learning ability improvement， this paper proposes reforms in teaching models such as classification and stratification of ordinary differential equations courses， fully leveraging the advantages of teaching teams， and utilizing online teaching platforms to achieve a student-centered teaching model as much as possible， and constructing a new evaluation system， integrating ideological and political elements at appropriate nodes to strengthen the guidance of ideological and political education in the curriculum. The study strives to achieve a teaching model that is more suitable for today's educational concepts and more in line with the characteristics of the student era through reform.

Keywords： Ordinary Differential Equations; core curriculum; classification teaching; layered teaching; team teaching

常微分方程是数学分析、高等代数等基础课程的后继专业基础必修课，同时又是偏微分方程、随机微分方程等课程的基础，在整个数学理论体系中起着非常重要的承上启下作用。随着科学的发展，数学应用的思想越来越受到重视。利用数学理论模型指导实验学科的实践也越来越被广泛推广。在每年的全国大学生数学建模竞赛题目中，总有使用常微分方程模型分析问题的题目。而这些题目很多就是科学研究问题中的一部分。比如，2020年辽宁省大学生数学建模竞赛的B题即为传染病传播问题，就是封闭系统传染病传播问题的研究，主要应用微分方程模型分析，而且传染病传播目前仍是科学研究的一个重要研究课题。鉴于常微分方程在科学研究方面的重要作用，数学相关专业的研究生复试中，常微分方程基本上都是其中的一个复试科目。

塞蒙斯曾这样评价微分方程在数学中的地位：300年来分析是数学里首要的分支，而微分方程又是分析的天然后继课程，又是为了解物理科学的一门最重要的数学，而且在它所产生的较深的问题中，它又是高等分析里大部分思想和理论的根源[1-2]。

常微分方程课程非常重要，其课程授课的时间也基本上安排在学生修了必要的数学分析、高等代数以及解析几何等基础课部分或者全部内容之后。虽然教学模式也在不断尝试改革，但是，随着网络时代的发展，以及学生接触到爆炸性资源的环境下，如果利用好先进的网络教学平台，发挥学生的课堂主题能动性，体现教师的主导性，提高学生的数学素养等，还需要任课教师和任课教师团队认真思考，查阅资料，认真准备，设计好每一堂课的教学内容。

一" 常微分方程核心课程建设要求

河南大学数学与统计学院共设置有数学与应用数学、信息与计算科学、金融数学和统计学四个专业，其中数学与应用数学专业是河南大学传统优势专业，2005年获批河南大学首批名牌专业，2007年批为河南大学特色专业。另外该专业2014年单设的“明德计划”实验班则是为了实施大众化背景下的精英教育，力争将学生培养成“厚基础、宽口径、重素质、强能力、有特色，在数学及其交叉学科具有巨大发展潜力”的高素质复合型卓越人才。开设于2000年的信息与计算科学专业是河南省设立最早的信息与计算科学专业，2011年获批为河南省特色专业，2019年获批河南省一流专业建设点。信息与计算科学专业围绕新工科建设发展战略，以数学和信息科学为基础进行交叉融合培养，在培养过程中的高年级阶段实施分模块教学，力争培养掌握良好信息技术或科学计算能力的高级人才。2021年获批国家级一流专业建设点的统计学专业也在高年级阶段实施分模块教学，分成数理统计模块与应用统计模块，有意识地根据学生的升学或就业意愿分别突出培养学生统计理论方法和统计软件操作能力。金融数学专业主要培养学生利用数学建模、数值计算等定量分析研究金融市场内在规律，熟练掌握金融工程、计量经济和保险精算等方面专业知识。

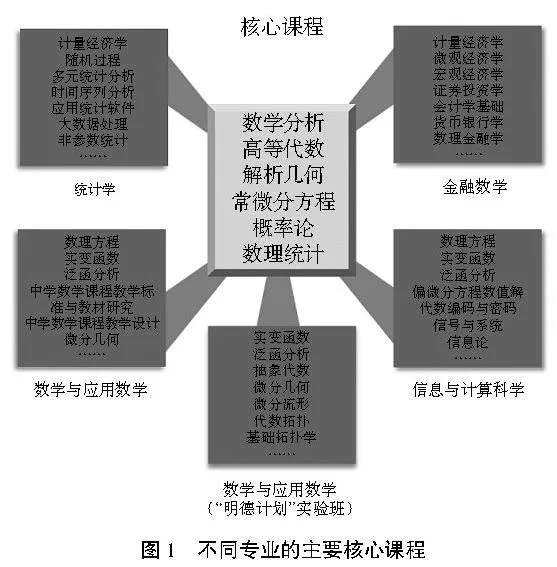
虽然每个专业都各有培养学生的要求和特点，但是都有共同的目标：主要培养学生具有良好的数学素养。作为数学大类专业，在各专业的培养方案中，分别设置以专业特点为背景而有所偏倚的核心课程（不完全列举如图1所示），其核心课程包括数学分析、高等代数、解析几何、常微分方程、概率论和数理统计。前三门作为数学基础课程的地位无可撼动，常微分方程也越来越受到重视，这与常微分方程身兼基础理论和应用研究的双重地位分不开。

打破以往照本宣科、只讲授课本内容的传统授课方式，加入当前学科研究最新进展中用到的常微分方程模型，通过背景介绍、方法介绍、模型建立、模型分析和问题应用，让学生感受到理论与实际科学研究的紧密结合，提升课程内容的新颖性，提高学习内容的挑战度，开拓学生的创新探索思维，尝试基于一些当前应用领域的研究背景建立微分方程模型，将学科研究新进展、实践发展新经验、社会需求新变化纳入课程，增强课程内容的“高阶性”“创新性”。以学习产出为导向，明确课程对培养目标达成度的贡献，细化课程对学生知识、能力、素质培养的教学目标与任务，开展课程教学达成度评价，并依此对课程进行持续改进。

二" 改革的重要方面

（一）" 利用线上平台，开展线上线下混合式教学

改变传统的单纯教室上课模式，利用线上教学平台，采用混合式新型教学模式;深化教学模式融合创新。主动适应高等教育的新形势，在学校课程数字化建设与管理平台建设完整课程，积极探索新形态课程建设。加强研究性、项目化、探究式和参与式教学，推广翻转课堂，充分运用现代化的信息技术手段，强化教学形式的先进性和互动性[3]。

在新冠病毒感染疫情的网课阶段，各种在线平台蜂拥出现。在之前的教学过程中，已经尝试使用雨课堂、智慧教室、钉钉课堂及腾讯会议等在线平台为学生开展过教学工作（如图2所示），任课教师逐渐感受到线下教学与线上教学的不同以及各自的优劣。随着在线教学平台的逐渐完善、任课教师对线上教学平台的使用方法熟练掌握以及学生电子产品的更新，使得发挥线上线下各自特长的融合教学更加受师生欢迎。

尽量丰富教学资源。建设和积累可以不断更新的电子教材、授课录像、网络课件、案例库、试题库和参考资料等在线课程资源，为学生提供丰富的自主学习资源。

（二）" 团队教学和分类教学

常微分方程课程团队主要有6名教师，其中1名教授，5名副教授。团队教师的研究领域包括偏微分方程、交叉学科以及生物统计等。每位教师不仅有丰富的教学经验，而且对常微分方程的理论掌握得非常扎实，对常微分方程在各自研究领域的应用都了然于心。课程团队结构合理，在对话访学交流或国内外学术会议中，善于与国内外著名高校的师资开展教学交流，充分发挥团队教师的特长，根据学生的专业特点和培养要求，分配合适的任课教师，构建分层次、分专业特长的课程团队。

打破以往课程团队机械分段、随意分工的授课模式，从科学前沿、基础理论、实践训练和学业拓展等环节进行合理分工，充分利用不同教师的优势，全面提升课程质量。比如做偏微分方程方向的教师，对常微分方程在偏微分方程等更深层次的数学理论体系中的基础和相互关联会体会更深，更加适合对数学与应用数学专业的学生开展教学，可以从理论基础到理论深度、理论难度方面拓展。再比如做数学交叉方向的教师，则适合对信息与计算科学、金融数学专业开展教学，以自己研究领域的最新常微分方程应用为例，开展启发式教学，更能加深学生对应用领域和科学研究的兴趣。另外，做统计相关研究方向的教师则更加适合对金融数学、统计学等专业的学生开展教学，将分析确定性问题的常微分方程理论拓展到随机微分方程理论，以及用微分方程理论开展数据分析等方面可以更加熟练的引申[4-6]。

总之，根据教师团队每位教师的研究特点和特长，结合四个专业的不同培养要求和特点，开展分类教学，不仅适合学生的培养要求，更能让学生在潜移默化中感知常微分方程课程在不同领域中的推广与应用，培养学生成为创新型、应用型人才。

（三）" 分类、分层教学

本科生在校学习的态度会随着时间变化，其学习目标也会影响学习动力。怎样提高学生的学习动力也是教学过程中需要注意的重要方面。而学习目标主要因就业前景而发生变化。数学与统计学院的学生目标主要由三类组成：考研究生，考公务员或考教师等事业单位编制以及就业。一年级学生中大部分可能只是关注考试修学分，二年级开始会有较多的学生开始考虑今后的发展目标。教学过程中引导学生明确目标，根据学生的需求和对不同学科的不同培养目标，制定分层教学计划。尽量改变传统的统一考核模式，采用分类考核，丰富考核形式，建立以激发学习动力和专业志趣为着力点的评价制度，进而逐步完善课程的考核形式。通过线上、线下平台提供开放性问题，启发学生开创性回答，加强对学生课堂内外、线上线下学习的评价，鼓励开展非标准答案考试，提高过程性评价在学业考核成绩中的比重，激发学生学习的积极性和思维的创造性，展示学生自主学习能力。对不同目标的学生实施不同的考核方式，对不同学习能力的学生采用合理的分层考核方式[7-9]，让学生的能力充分得到发挥，进而能够在今后的学习和工作中实现各尽其能。

（四）" 适当的课程节点融入课程思政元素

习近平总书记在全国高校思想政治工作会议上强调，“提升思想政治教育亲和力和针对性，满足学生成长发展需求和期待，其他各门课都要守好一段渠、种好责任田，使各类课程与思想政治理论课同向同行，形成协同效应”。常微分方程作为整个数学类课程体系中最重要的一块儿“责任田”，一段承上启下的“渠”，转任教师不仅要用“学高为师”的深理论灌输给学生，还要用“德高为范”的思想品德和价值观引领学生的世界观、价值观和人生观。在授课的合适节点上融入思政元素，加强课程思政引领，将思想价值引领贯穿于教学全过程，这个教学全过程不局限于常微分方程这一门课程，可以延伸拓展到前期或后继课程[9-10]。比如常微分方程第二章中将介绍伯努利方程，自然很多同学或听众听到此处都会认为“伯努利”是一个人名。确实，“伯努利”是人名，但是主要是人名中的姓氏。伯努利这个科学史上的伟大家族，是17—18世纪瑞士的一个出过多位数理科学家的家族。伯努利微分方程和概率论中的伯努利试验、伯努利大数定律主要是由雅各布·伯努利提出，而且雅各布也被公认为是概率论的先驱之一，是世界上最早使用“积分”这个术语的人。利用伯努利家族[11]（如图3所示）的数学故事引起学生对科学研究的兴趣，进而将学科知识进行一次大串联，并且引导学生树立远大理想，做敢担当、能吃苦、肯奋斗的新时代青年。

根据课程所属学科性质特点，结合教学内容实际，修订教学大纲，明确思想政治教育的拓展重点，在合适的教学节点融入载体，不断改善教学方法，不断制作更新课件，让内容更符合时代气息。将价值导向与课程知识传授相融合，在知识传授和能力培养中，引导学生自觉弘扬和践行社会主义核心价值观，不断增强“四个自信”，让学生树立正确的价值观和人生观。

三" 结束语

常微分方程在数学类专业课核心课程中起着承上启下的重要作用，本文旨在从理论上梳理教学改革的主要方面，进而在教学过程中开展实践工作。通过分类教学、分层教学，搭建实时更新的线上教学平台，丰富题库建设，充分发挥团队的优势，做好课程思政，对学生因材施教，真正实现“宽口径、重素质”的学生培养模式。

参考文献：

[1] 塞蒙斯G.F.微分方程[M].张理京，译.北京：人民教育出版社，1981.

[2] 王高雄，周之铭，朱思铭，等.常微分方程[M].4版.北京：高等教育出版社，2020.

[3] 袁锐.“常微分方程”课程线上线下混合式教学模式探析[J].教育教学论坛，2020（38）：248-249.

[4] 崔仁浩，刘萍.“常微分方程”课程启发式教学初探[J].继续教育研究，2016（3）：119-121.

[5] 李晨松.基于师范专业认证的常微分方程教学模式改革探究[J].内蒙古民族大学学报（自然科学版），2021，36（2）：171-174.

[6] 王振国.本科院校《常微分方程》课程的教学改革与实践[J].教育理论与实践，2015，35（21）：56-57.

[7] 吴楚升.《常微分方程》课程分层教学的实践分析与探究[J].开封教育学院学报，2019，39（3）：112-113.

[8] 李姝敏，郭鹏云，徐国明.常微分方程课堂教学改革的探索与实践[J].赤峰学院学报（自然科学版），2023，39（3）：88-92.

[9] 陈光霞，李凤萍.课程思政理念在《常微分方程》教学改革中的应用[J].高等数学研究，2022，25（1）：102-104.