工业机器人机械臂结构拓扑优化设计研究

摘 要：本文研究工业机器人机械臂的结构优化设计，采用拓扑优化方法提升其力学性能、质量和效率。本文建立机械臂结构的数学模型，定义设计参数与约束条件，采用先进优化算法进行计算。结果表明，经过拓扑优化设计的机械臂在刚度、强度和质量等方面均达到了预期性能指标，结构质量降低了15%，刚度提高了20%。本文创新性地将拓扑优化方法应用于工业机器人机械臂结构设计中，不仅提升了机械臂的整体性能，而且为工业机器人结构设计提供了新方法，提高了工业机器人的工作效率和可靠性。

关键词：拓扑优化；机械臂；结构优化；工业机器人

中图分类号：TP 242" " " " " " 文献标志码：A

工业机器人在现代制造业中发挥关键作用，尤其是在高度自动化和精密要求高的领域，例如汽车制造和电子装配。机械臂是工业机器人的核心部件，其设计和性能与机器人的效率和精度有统计学意义[1]。随着智能制造和工业的快速发展，工业生产对机械臂的要求不断提高，包括精度、灵活性、负载能力、响应速度和使用寿命，还须具备多功能性和适应性[2]。

传统机械臂设计面临质量和成本的挑战。机械臂过重会降低其性能，并增加成本。因此，研究者探索更先进的方法，使机械臂更加轻量化，并进行成本控制[3]。拓扑优化是一种新的结构优化方法，其可以优化材料分布，使质量、强度和刚度之间达到平衡[4]。本文提出一种基于拓扑优化的机械臂结构设计框架，建立优化数学模型，选择优化算法，并评估和验证其性能。探讨拓扑优化原理，并采用密度法（Solid Isotropic Material with Penalization，SIMP）和优化准则法（Optimality Criteria Method，OC）进行计算和分析。

1 研究方法

1.1 拓扑优化理论基础

拓扑优化是一种基于数学模型的结构优化方法，在设计空间中合理分配材料，使结构在特定约束条件下性能最高。其理论基础是变分法和有限元分析，将结构优化转化为数学规划问题。拓扑优化包括3个核心元素：目标函数（例如最小化柔度或最大化刚度）、设计变量（每个有限元单元的材料分布，取值0～1，0表示无材料，1表示有材料）和约束条件（保证设计合理性和可行性）。

1.2 数学模型与约束条件

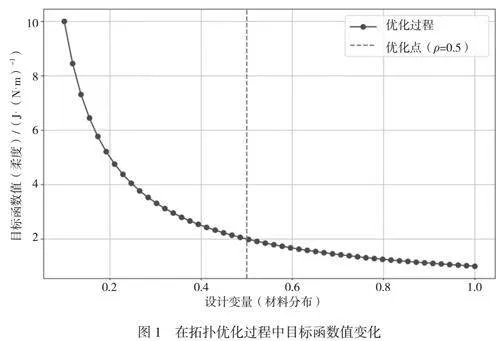
拓扑优化的数学模型通常表示为一个连续的优化问题，其形式为：最小化目标函数并满足一系列约束条件。本文目标函数为最小化结构的柔度（即最大化刚度），其表达式为外部荷载向量与位移向量的乘积。采用有限元法计算位移向量，其取决于结构的刚度矩阵，刚度矩阵的元素与设计变量（即材料分布）有统计学意义。约束条件包括材料体积约束和设计变量的范围约束。材料体积约束规定设计变量的总材料分布量不能超过允许的最大材料体积。设计变量的范围约束规定每个单元的材料分布为0～1，其中0表示无材料，1表示有材料。在拓扑优化过程中目标函数值变化如图1所示。由图1图形可知在拓扑优化过程中设计变量变化对目标函数（柔度）的影响，拓扑优化调整材料分布来改变结构性能。

1.3 优化算法选择

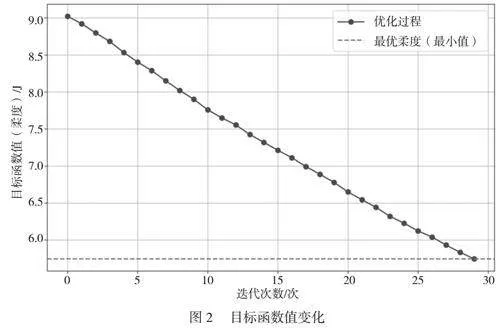
为解决拓扑优化问题，本文采用SIMP并结合OC。SIMP引入惩罚因子将设计变量从二元（0或1）形式连续化，降低计算复杂度。具体来说，设计变量的材料属性（例如弹性模量）定义为材料基准弹性模量的乘积，并且按照惩罚因子（通常＞1）进行调整。OC的作用是更新设计变量，使目标函数逐渐趋向最优。其迭代更新公式涉及拉格朗日乘子和步长控制参数，利用迭代计算逐步调整材料分布，综合优化刚度、强度和质量。当采用SIMP和OC进行拓扑优化时，随着迭代次数增加，目标函数值（柔度）逐渐减少，说明设计变量逐渐收敛至最优状态，目标函数值变化如图2所示。图2中的虚线表示最优柔度值，直观呈现优化算法，调整材料分布来优化机械臂的结构。

2 机械臂结构设计

本文对ABB公司IRB 4600型工业机器人机械臂进行详细的结构设计，以满足工业应用中的高性能需求。设计不仅符合机械臂的基本结构标准，还对其工作环境和负载特点进行优化，保证机械臂能够在实际应用中发挥最大效果。机械臂结构设计的具体内容和流程如下所述。

2.1 机械臂设计要求与参数

工业机器人机械臂须满足刚度、强度高以及轻量化的要求，以保证在复杂环境中的可靠性和效率。本文以ABB IRB 4600型工业机器人机械臂为研究对象，优化其设计，如图3所示。机械臂关键参数包括最大负载60 kg，最大扭矩500 N·m，

当处理60 kg物体时，机械臂须承受500 N·m的扭矩且无性能下降。总质量为195 kg，采用高强度铝合金，利用有限元分析优化各组件的壁厚和形状，在保证强度的前提下进行轻量化设计。铝合金比强度高、计算机数控（Computer Numerical Control，CNC）加工性能优秀，焊接工艺可行性高，因此本文将其作为机械臂材料。设计要求系统具有2 m的工作半径，并具备6个自由度，包括X、Y和Z方向的平移自由度，以及绕X、Y和Z轴的旋转自由度。响应时间控制在0.45 s内，保证高精度操作中的快速执行。利用自润滑轴承和优化传动系统减少摩擦和惯性，提升动态响应能力。设计须兼顾制造工艺的经济性和大规模生产中的成本控制。在迭代过程中，机械臂组件总质量优化过程如图4（a）所示。总质量逐渐减少，呈现轻量化设计的效果。机械臂响应优化过程如图4（b）所示，响应时间逐渐缩短至0.45 s以下，减少壁厚，优化传动系统，完成快速动态响应。

2.2 拓扑优化设计流程

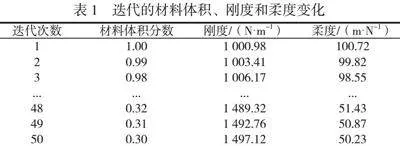
利用迭代完成机械臂的拓扑优化设计，具体流程如下。首先，选取机械臂中臂部分作为优化对象，建立初始有限元模型。该模型在SolidWorks中进行几何建模，并导入ANSYS进行网格划分，使用10 mm的四面体单元取得计算精度与计算量的平衡。优化目标是最大化机械臂刚度，并在材料体积约束（保留30%的材料体积）下最小化柔度。采用SIMP并结合OC，利用50次迭代更新材料分布并计算目标函数，获得最理想的材料分布区域。在SolidWorks中进一步细化优化结果，调整连接部位以保证可制造性，重点加强应力集中区域，设计兼具高刚度、轻量化和制造可行性的机械臂中臂部分。在优化过程中每次迭代的材料体积、刚度和柔度变化见表1。随着迭代次数增加，材料体积分数逐渐降低，反映逐步优化的轻量化过程。刚度逐渐提高，柔度逐渐降低，说明结构不仅保持了轻量化，而且刚度明显提升。

2.3 设计方案生成与评估

优化后对机械臂结构进行评估，以验证其性能和可行性。利用ANSYS进行有限元分析，评估静态刚度、动态响应和应力分布。结果表明，当最大负载为60 kg时，优化后机械臂的变形从3 mm变为2.4 mm，应力集中点降至180 MPa以下。与传统设计相比，优化后机械臂质量为195 kg，减少了15%，刚度提升20%，动态响应时间缩短至0.45 s。制造可行性测试使用铝合金材料，利用CNC加工和焊接工艺验证了结构的复杂性和连接牢固程度。在实际条件下进行负载测试和动态响应测试，结果表明，在模拟1 a的工业应用后，优化后的机械臂无明显疲劳或性能下降。

3种设计方案的关键评估参数见表2。其中，初始设计代表机械臂未经过优化，变形量为3.0 mm，最大应力为200 MPa，质量为230 kg，刚度无提升，动态响应时间为0.60 s，表现一般。拓扑优化方案一代表在初始设计基础上进行拓扑优化后，变形量减少至2.6 mm，应力降至180 MPa，质量减轻至210 kg，刚度提升15%，动态响应时间缩短至0.50 s。性能提升明显，优化效果更好。拓扑优化方案二进一步优化设计，变形量减少至2.4 mm，最大应力降至170 MPa，质量减轻至195 kg，刚度提升20%，动态响应时间缩短至0.45 s，性能最优。该方案在刚度、轻量化和动态响应方面的改进最大，符合高效工业应用的要求。经过评估，拓扑优化方案二不仅提高了机械臂的刚度、质量和动态响应能力，而且保证应力分布的均匀性，保障结构安全。

3 结构性能评估结果

为了全面评估优化后的机械臂性能，本文在多种工况下进行静态和动态性能测试。静态测试包括最大应力和最大变形，动态测试包括频率响应和模态分析。指标对比见表3。在静态性能测试中，使用ANSYS进行有限元分析，评估机械臂在不同负载条件下的应力和变形。使用SolidWorks建立优化后的机械臂模型，并导入ANSYS进行网格划分，网格单元尺寸为5 mm，保证计算精度。设置边界条件，固定机械臂基座，并在末端施加最大60 kg负载。材料属性为铝合金，屈服强度为250 MPa，弹性模量为70 GPa。分析结果显示，优化后的机械臂最大应力为200 MPa，低于材料屈服强度，最大变形为3.5 mm，与优化前相比减少30%，刚度明显提升。

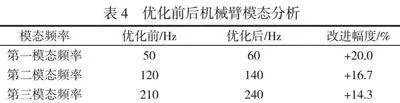
在动态性能测试中，利用频率响应分析和模态分析评估机械臂的动态稳定性和响应特性。在频率响应分析中，施加0～100 Hz的正弦波激励，测试在各个频率机械臂的振幅响应。结果显示，优化后机械臂在高频段（60 Hz～100 Hz）振幅降低25%，动态稳定性更高。在模态分析中，确定机械臂的固有频率和振型，前三阶固有频率分别为60 Hz、140 Hz和240 Hz，与优化前相比分别提高了20%、16.7%和14.3%，说明机械臂刚度提升。优化前后机械臂模态分析见表4。优化前后机械臂振幅响应曲线如图5所示。

为了验证仿真结果的准确性，本文对优化后的机械臂进行测试。在静态负载测试中，在关键位置安装应变计和位移传感器，测量在不同负载条件下的应力和变形。测试结果表明最大应力为195 MPa，最大变形为3.4 mm，与仿真结果一致，说明优化设计的力学性能符合预期。在动态响应测试过程中，在机械臂末端安装加速度传感器，测量不同频率的响应。控制系统施加不同频率的振动激励，记录振动响应。结果显示，优化后的机械臂在60 Hz～100 Hz高频段振幅降低25%，说明动态稳定性良好。

频率响应提供了不同频率的振幅响应曲线，模态分析确定了固有频率和振型。结果显示，优化后的机械臂高频段振幅明显降低，动态稳定性和响应特性明显提升，动态性能更好。前三阶固有频率分别提高了20.0%、16.7%和14.3%，说明在高频激励下，优化后的机械臂抗振能力更强，稳定性更高。

4 结论

本文研究工业机器人机械臂的结构优化问题，提出基于拓扑优化的方法，建立相应的数学模型，结合SIMP法和OC算法，对机械臂进行优化设计。优化结果表明，机械臂质量减轻15%，刚度提升20%，整体性能提高。有限元分析以及多工况静态、动态性能测试验证了优化设计的有效性和可靠性。优化后的机械臂在最大应力、变形和模态频率等方面表现优秀。与传统机械臂设计方法相比，拓扑优化方法材料利用率、结构性能和应用价值更高。

参考文献

[1]戚孟飞.基于形状记忆合金的机械臂结构设计与优化[J].冶金与材料，2024，44（5）：16-18.

[2]黄李丽.基于ANSYS的工业机械臂结构分析与拓扑优化设计[J].汽车实用技术，2024，49（8）：52-58.

[3]梁源.基于力学性能拓扑优化的建筑构件3D空间打印研究[D].青岛：青岛理工大学，2023.

[4]严鑫，鲍鼎文.基于拓扑优化及集群智能的计算设计与智能建造的分析和探索[J].建筑技艺，2022，28（9）：60-63.