基于改进三元模型的波纹管型气动软体驱动器神经网络滑模控制

摘要：针对一款波纹管型气动软体驱动器，提出了一种基于改进三元模型的滑模控制方法，并使用RBF神经网络补偿扰动以实现该型驱动器在竖直方向上对期望轨迹的跟踪控制。首先搭建波纹管型气动软体驱动器实验平台，测试并分析该驱动器的动态特性，基于上述动态特性提出波纹管型气动软体驱动器的改进三元模型；然后利用采集到的实验数据，基于最小二乘算法对其进行参数辨识，从而获得所提模型的参数；进而结合改进三元模型设计滑模控制器，使用RBF神经网络对集总扰动进行补偿，并利用Lyapunov方法分析系统的稳定性；最后通过一系列实验验证了所提方法的有效性。

关键词：波纹管；气动软体驱动器；三元模型；滑模控制；径向基函数神经网络

中图分类号：TP273

DOI：10.3969/j.issn.1004132X.2024.08.010

开放科学（资源服务）标识码（OSID）：

Neural Network Sliding Mode Control of Bellows-type Pneumatic Soft

Actuators Based on Improved Ternary Model

LYU Boyang1，2，3 MENG Qingxin1，2，3 XIAO Huai1，2，3

LAI Xuzhi1，2，3 WANG Yawu1，2，3 WU Min1，2，3

1.School of Automation，China University of Geosciences，Wuhan，430074

2.Hubei Key Laboratory of Advanced Control and Intelligent Automation for Complex Systems，

Wuhan，430074

3.Engineering Research Center of Intelligent Technology for Geo-Exploration，Ministry of Education，

Wuhan，430074

Abstract： A sliding mode control method was proposed based on an improved ternary model for a bellows-type pneumatic soft actuator， and an RBF neural network was used to compensate the aggregate set disturbance to achieve tracking control of the desired trajectory in the vertical direction of this type of actuators. Firstly， an experimental platform was constructed to test and analyse the dynamic characteristics of the bellows-type pneumatic soft actuators. Based on the above dynamic characteristics， an improved ternary model of the bellows-type pneumatic soft actuators was proposed. Meanwhile， the parameters of the proposed model were obtained by using the collected experimental data for parameter identification based on the least squares algorithm. Then， the sliding mode controller was designed in conjunction with the improved ternary model， and the RBF neural network was used to compensate for the aggregate set disturbance. The stability of the system was analysed by using the Lyapunov method. Finally， the effectiveness of the proposed method was verified through a series of experiments.

Key words： bellow; pneumatic soft actuator; ternary model; sliding mode control; radial basis function（RBF） neural network

0 引言

软体机器人是近年来机器人领域新兴的重要研究方向，因复杂环境适应、人机交互等方面具备的独特优势而备受关注［1］。软体驱动器作为软体机器人实现运动所需的关键组件，直接决定了软体机器人的特性和性能，是软体机器人领域的重要研究对象之一。

软体驱动器通常可根据其驱动方式划分为线驱动型、电驱动型、磁驱动型与流体（气/液）驱动型等，其中，气动软体驱动器［2］因具有柔顺性好、安全性高、价格便宜、易于维护等优势而受到研究人员青睐［3］。目前，已有多种气动软体驱动器被设计并应用在软体机器人上。张立彬等［4］设计了一款气动柔性球关节，应用在多指灵巧手上。TONDU等［5］设计了一款气动人工肌肉驱动的七自由度仿人机械臂。POLYGERINOS等［6］设计了一款运用气动软体驱动器的康复手套。根据其形变方式，气动软体驱动器具有弯曲型、伸缩型、膨胀型等多种类别，其中，伸缩型气动软体驱动器形变量大，质效比高，泛用性强，可以通过多驱动器组合的形式完成伸缩、弯曲、扭转等多维度运动［7］，具有很高的研究价值。

当前，气动人工肌肉与波纹管型气动软体驱动器是比较有代表性的两类伸缩型气动软体驱动器。气动人工肌肉由一根柔软的空心橡胶软管及管外覆盖的一层纤维网格套筒构成，其形变原理主要依靠不可拉伸的纤维网格套筒将内部空心橡胶软管的径向膨胀转化为轴向收缩。这种形变方式使气动人工肌肉可以承受较大的气压，具有高输出力和快速响应的优点。目前，针对气动人工肌肉的研究已较为丰富［8-11］。然而，气动人工肌肉的形变方式也使其在运动的过程中径向膨胀明显，在一些空间受限的应用场景中，其适用性大打折扣。波纹管型气动软体驱动器解决了这一问题，它由多个波纹状气室串接而成，其形变主要依赖于波纹状气室的膨胀和收缩。得益于气室的波纹形状，它在轴向伸缩时不会带来明显的径向变形。这种形变方式也使其可以在较小驱动气压的情况下实现较大的形变，效率高且抗扭转性能好。虽然波纹管型气动软体驱动器的输出力稍弱于气动人工肌肉，但依靠上述优势，它在软体机器人领域已有许多成功的应用实例［12-14］。然而，当前针对波纹管型气动软体驱动器的建模和控制研究，尤其是目标轨迹跟踪控制研究还不太充分。

由于上述两类伸缩型气动软体驱动器的工作原理不同，直接将现有的气动人工肌肉控制方法应用于波纹管型气动软体驱动器显然会导致较差的控制效果，故针对波纹管型气动软体驱动器的建模和控制研究仍是一个挑战性的课题。此外，考虑到波纹管型气动软体驱动器整体采用软材料制成，缺少刚性结构的支撑，当其在水平面运动时，其自身形状易受重力的影响而产生弯曲变形，从而影响驱动器性能与控制精度。本文针对波纹管型气动软体驱动器在竖直平面的运动跟踪控制展开研究。

目前，针对气动软体驱动器的控制方法大致可划分为无模型的控制方法与基于模型的控制方法。其中，无模型的控制方法不依赖于目标气动软体驱动器的具体数学模型，而是基于状态信息直接构建控制律。该类型控制方法包含PID控制［15］、神经网络控制［16］等。WU等［17］运用PID模糊控制器实现了对气动人工肌肉驱动的穿戴式人工机械手的轨迹跟踪控制。AHN等［18］设计了一款神经网络控制器，能够使拮抗式气动人工肌肉达到目标角度。总体上来说，尽管无模型控制器不需要依赖系统模型参数，但由于缺乏所研究系统的模型与先验知识，故无模型控制器的规划能力并不强，往往难以胜任需要精确控制的任务。

基于模型的控制方法则通过引入所研究系统的模型，针对性地设计控制器以给出精确的控制指令，因此在模型准确的情况下，基于模型的控制方法一般精度较高。该类型的控制方法又可划分为基于运动学模型的控制方法以及基于动力学模型的控制方法。其中，基于运动学模型的控制方法从几何学的角度研究机器人运动规律，注重控制对象的目标运动和每个驱动单元运动之间的关系，如张启航等［19］对一款仿象鼻气动连续体机器人进行运动学建模，实现了对其的位姿控制。此类控制方法在位置控制或者弯曲角度控制上十分有效，但由于未考虑系统的惯性与受力情况等因素，故在高速运动、目标轨迹跟踪等应用上的控制效果较差。

基于动力学模型的控制方法关注被控对象的运动和驱动单元输入力或力矩的关系，包含对系统速度及加速度的描述，因此这类控制方法更加适用于连续运动与跟踪控制，如YAN等［20］基于气动位置伺服模型设计LQR最优控制器，实现了对一款垂直跳动气动执行器的稳定控制。然而，在针对波纹管型气动软体驱动器的控制研究中，当前基于动力学模型的控制方法还存在以下挑战：一方面，软体材料具有黏弹性，这导致气动软体驱动器的运动表现出复杂的迟滞特性，其精确的具有严格物理意义的动力学模型很难被建立。研究人员尝试基于唯象建模的理论来建立气动软体驱动器的动力学模型，其中，三元模型是一种经典的唯象模型［21］，常用于描述气动人工肌肉的运动特性。该模型将软体驱动器的黏弹性用一个弹簧单元、一个阻尼单元与一个施力单元组合的形式来描述，这些单元的参数与驱动器的输入气压有关。然而，波纹管型气动软体驱动器的运动方式与气动人工肌肉不同，更易受负载质量的影响。传统三元模型未考虑负载质量与模型参数之间的耦合效应，往往难以准确描述波纹管型气动软体驱动器的动态特性。另一方面，气动软体驱动器的唯象模型参数往往是基于实验数据辨识得到的，辨识结果不可避免地会存在辨识误差。此外，由于气动软体驱动器自身的材质特性，其动态特性易受外部大气压、振动、气流等外部扰动的影响，这些因素可以被视为系统的不确定性。然而，当前一些基于动力学模型的控制方法较少考虑这些系统不确定性的影响，其鲁棒性较差。

本文针对一款波纹管型气动软体驱动器进行研究，提出了一种基于改进三元模型的神经网络滑模控制方法，使其能够对驱动器在竖直方向上的运动进行高精度控制的同时，对运行过程中的各种不确定性具有较强的抗扰动性能。本文搭建了实验平台，对波纹管型气动软体驱动器的动态特性进行了分析；基于驱动器动态特性，在传统三元模型的基础上提出改进三元模型并对其进行了参数辨识；结合改进三元模型，设计滑模控制器，并使用径向基函数（radial basis function，RBF）神经网络补偿系统集总扰动，运用 Lyapunov函数验证了系统的稳定性；最终通过实验来验证所提方法的有效性与先进性。

1 实验准备

1.1 实验平台的搭建

本文使用自制的波纹管型气动软体驱动器进行实验。为了实现对其在竖直方向上运动的数据采集与轨迹跟踪控制，搭建了波纹管型气动软体驱动器实验平台，如图1所示。实验平台由以下装置组成：①计算机（CPU：i9-12900KF），用于计算控制信号L及显示波纹管型气动软体驱动器状态参数（内部气压p与活动端位移x），采样时间设置为0.01 s；②波纹管型气动软体驱动器（材质为硅胶，静态长度158 mm，最大静态外径60 mm，自重133.7 g，安全受压范围0～60 kPa）；③比例压力调节器 （型号：VPPI-5L-3-G18-1V1H-V1-S1D，制造商：Festo，输出范围-0.1～0.6 MPa），用于调节并实时反馈波纹管型气动软体驱动器内部气压p；④I/O模块（型号：PCIe-6363，制造商：National Instruments），用于连接计算机与系统仪器；⑤正压气泵（型号：OTX-550X3，制造商：奥突斯，容积65 L），用于给实验平台提供稳定正气压源；⑥负压气泵 （型号：JBL-750，制造商：佳宝丽，容积36 L），用于给实验平台提供稳定负气压源。

实验平台的运作流程如下：计算机内部经由一系列计算得到控制气压pC，然后经比例关系式L=αpC（α为比例压力调节器比例系数，αgt;0）得到控制信号L，并通过 I/O 板卡将此信号传输到比例压力调节器。比例压力调节器根据控制信号L调节波纹管型气动软体驱动器的内部压力p，使得p～pC。在p的作用下，波纹管型气动软体驱动器活动端将在竖直方向上运动，产生位移。波纹管型气动软体驱动器运动示意图见图2。

1.2 系统动态特性的分析

为了对波纹管型气动软体驱动器进行精确建模，进行多组实验并采集数据，以分析波纹管型气动软体驱动器在竖直方向运动的动态特性。

考虑到对于驱动器建模与控制的需求，分析了输入气压频率与负载质量对波纹管型气动软体驱动器动态特性的影响。

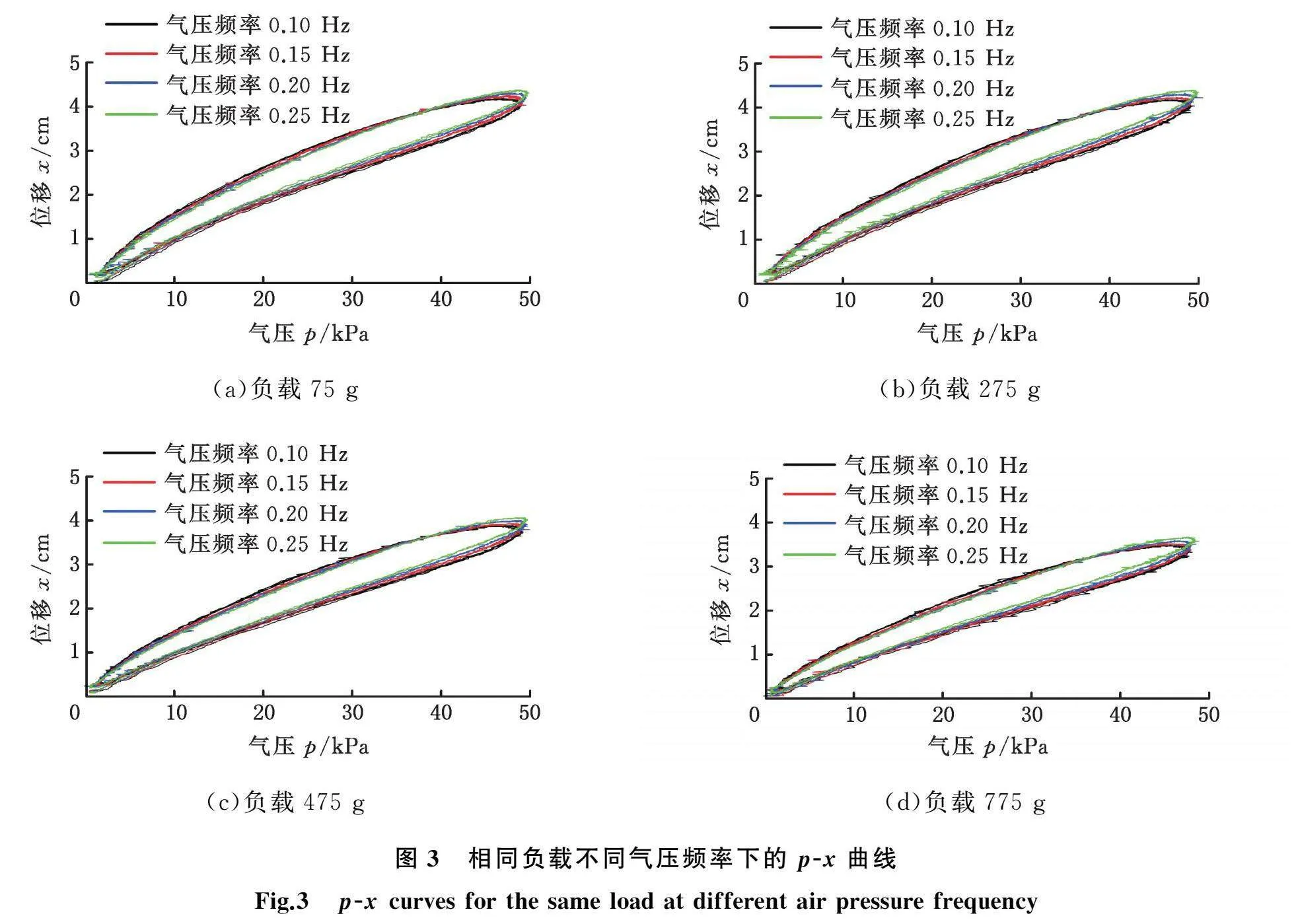
首先对输入气压频率与负载质量变化范围进行选择。考虑到本文实验中使用的波纹管承载能力有限，当悬挂的负载超过1 kg时，驱动器会产生极限拉伸，在后续的充气过程中将无法再产生明显的形变，为了避免对驱动器的性能造成严重影响，同时使各组数据之间产生较为明显的对照效果，设置0、200 g、400 g、700 g四组质量的砝码来作为实验负载。此外，本文使用的波纹管型气动软体驱动器移动端部件为3D打印的砝码吊筐，其自重为75 g，因此在实验中的实际负载质量为75 g、275 g、475 g、775 g。由于本实验中波纹管型气动软体驱动器通过导气软管供气，单位时间气体流量有限，为了保证波纹管内实时气压能够跟上控制信号的变化，控制信号的输入频率应限制在0.3 Hz以下的低频段。因此，设置0.10 Hz、0.15 Hz、0.20 Hz、0.25 Hz四组输入气压频率的正弦波信号。记录每组实验中波纹管内部压力p与驱动器活动端位移x的数据，如图3、图4所示。

由图3可看出，在不同的载荷质量条件下，随着输入压力变化频率的提升，p-x曲线表现出逐渐收缩的趋势，但整体变化并不明显，可知在低频段，输入压力频率对波纹管型气动软体驱动器动态特性的影响相对较小。而在输入频率相同的情况下，载荷质量的变化则使p-x曲线出现较为明显的偏移，图4较为直观地展示了这一现象。可见，负载质量变化对波纹管型气动软体驱动器的动态特性有较为明显的影响，这主要是因为随着负载质量的增加，波纹管驱动器的预拉伸程度会增大。由于波纹管驱动器在竖直方向上的形变主要依赖于充放气过程中波纹状气室的膨胀和收缩（图2），当波纹状气室的预拉伸位移量增大时，其继续膨胀的能力就会减弱，表现为波纹管驱动器活动端的运动幅度缩小。

2 波纹管型气动软体驱动器建模

三元模型是一种描述轴向运动软体驱动器动力学的经典模型，但在传统的三元模型中，驱动器与负载被描述为相互独立的两个部分。根据上文对于驱动器动态特性的分析，波纹管型气动软体驱动器实际上与负载存在较为紧密的耦合关系。为此，本文尝试建立一种改进的三元模型，以更好地反映载荷质量变化对波纹管型气动软体驱动器动态特性的影响。

2.1 系统动态特性的分析

在传统三元模型中，波纹管型气动软体驱动器的动力学方程可被描述为［22］

Mx¨+B（p）x·+K（p）x=F（p）-Mg（1）

其中，M为载荷质量；x、x·、x¨分别为波纹管型气动软体驱动器活动端的位移、速度和加速度；B（p）和K（p）分别为三元模型中阻尼单元和弹簧单元的相关系数；F（p）为三元模型中施力单元所提供的力。B（p）、K（p）、F（p）可通过下式进行拟合：

B（p）=∑Ni=0Bip（i）

K（p）=∑Ni=0Kip（i）

F（p）=∑Ni=0Fip（i）（2）

一般而言，N越大，拟合精度就越高，模型复杂程度也越高。出于实际应用的考虑，一般取N=1，此时式（2）可写成

B（p）=B0+B1p

K（p）=K0+K1p

F（p）=F0+F1p（3）

式中，B0、B1、K0、K1、F0、F1为未知常数。

由于波纹管型气动软体驱动器具有较强的延展性，故在竖直方向上，运动过程中的载荷的质量将不可避免地影响驱动器的形变幅度与形变速度，进而影响其相关特性。根据文献［23］以及上文对实验系统静、动态特性的分析，可以发现波纹管型气动软体驱动器在竖直方向上的动态响应明显受载荷质量M变化的影响。由式（1）、式（2）可知，传统的三元模型中仅将Mg视为一个外力项考虑，而忽视了M对B（p）、K（p）、 F（p）的影响，当M发生改变时，传统的三元模型对波纹管型气动软体驱动器静、动态特性的拟合效果会变差。

针对以上问题，考虑在B（p）、K（p）、 F（p）的计算公式中加入载荷相关项以对传统三元模型进行改进，改进后的动力学方程为

Mx¨+B（p，M）x·+K（p，M）x=F（p，M）-Mg（4）

B（p，M）=B0+B1p+b0M

K（p，M）=K0+K1p+b1M

F（p，M）=F0+F1p+b2M（5）

其中，模型参数B0、B1、K0、K1、F0、F1、b0、b1、b2均为未知常数，为了获得它们的具体数值，基于采集到的实验数据，对这些参数进行辨识。

2.2 参数辨识方法

对于物理结构参数（如长度、粗细、硅胶厚度、波纹数等）不同的波纹管驱动器，无需改变改进型三元模型的模型框架，只需针对不同的波纹管驱动器开展数据采集，获取其活动端位移与输入气压的实验数据，并利用数据对改进型三元模型的参数进行重新辨识即可。

本文使用最小二乘方法对系统模型的未知参数进行辨识。由于使用的比例压力调节器的精度限制，当输入压力频率过低时，信号曲线整体平滑度将有所下降；而输入气压变化频率过高则会使系统框架发生较为明显颤动，干扰测量结果。由上文可知，负载质量对波纹管型气动软体驱动器的动态特性有显著影响，输入压力频率对其影响则相对较小，故选择实验数据较为稳定的0.2 Hz作为输入气压变化频率，记录多组不同载荷下的开环实验数据作为参数识别的依赖数据。

收集的数据包含实验中按时间顺序测得的驱动器活动端位移数据集X={x（1），x（2），…，x（N）}与内部气压数据集P={p（1），p（2），…，p（N）}（X、P的向量形式记为X、P），其中，N为数据集X中元素个数；x（k）为数据集X的第k个元素（k=1，2，…，N）；p（k）为数据集P的第k个元素。则系统的最小二乘格式可表示为

x（k）=f（p，θ）+e（k）（6）

θ=（θ（1），θ（2），…，θ（n））

其中，θ为被辨识的参数向量（n为参数向量中包含的参数个数）；函数f（p，θ）为通过式（4）、式（5），在其他变量为常数时获得的x与p之间的映射；e（k）为系统误差。可知准则函数J（θ）为

J（θ）=∑Nk=1（e（k））2=∑Nk=1（x（k）-hT（k）θ）2（7）

最小二乘法参数估计即通过最小化准则函数 J（θ）来寻找最优参数向量θ。设q=1，2，…，qm为当前迭代次数（qm为最大迭代次数），θq为第q次迭代后的模型参数向量；Xq=｛xq（1），xq（2），…，xq（N）｝是以θq作为模型参数、P作为模型输入，计算得到的位移数据集（其向量形式记为Xq），其中xq（k）为数据集Xq的第k个元素；误差向量Eq=X-Xq。每次迭代更新的准则函数为

Jq=∑Nk=1（x（k）-xq（k））2=ETqEq（8）

模型参数向量的更新值为

θq+1=θq-H-1qITqEq（9）

式中，Iq为雅可比矩阵；Hq为黑森矩阵。

设θ0为模型参数的初值，θm为模型参数的优化结果，σq为准则函数的梯度，σmin为准则函数梯度下限（为一足够小的正值）。则参数辨识算法的计算步骤如下：

（1）初始化，令q←1，置初值θ0=（0，0，…，0），J0=0。

（2）根据式（4）～式（6）计算Xq。

（3）根据式（8）计算Jq及Eq。

（4）根据式（9）计算θq+1。

（5） σq←Jq-Jq-1。

（6）如果qlt;qm或σqgt;σmin，则q++， 转到步骤（2）；否则结束运算，取得参数估计值θm。

2.3 不确定性的表示

对于波纹管型气动软体驱动器，还应考虑实验过程中存在的多种不确定性。受模型复杂程度与参数辨识精度的限制，系统模型与实际情况之间必然存在误差，将其设为模型误差dm。在控制过程中，由于气压测量精度的限制以及传递过程中的损耗，气动软体驱动器的内部压力p与输入的控制压力pC之间显然存在误差，可令pC=p+Δp，其中Δp为气动软体驱动器内部气压与控制气压之间的误差，即比例压力调节器的硬件调节误差。用pC替换式（4）中的p，将产生的设备扰动设为dp。实际实验中，气动软体驱动器亦可能受到外部扰动的影响，将系统外部扰动设为do。综上所述，式（4）可写成

Mx¨=-B（pC，M）x·-K（pC，M）x+

F（pC，M）-Mg+dt（10）

dt=dp+do+dm

其中，dt为系统的集总扰动项，本文中的控制项即控制气压pC，则式（10）可写成

x¨=z1（x，x·）+z2（x，x·）pC+d（11）

z1（x，x·）=［-（B0+b0M）x·-（K0+b1M）x+

（F0+b2M）］/M-g

z2（x，x·）=（-B1x·-K1x+F1）/M

d=dt/M（12）

3 波纹管型气动软体驱动器控制设计

本文的控制目标如下：设计控制律PC，使得波纹管型气动软体驱动器活动端的实际轨迹x在控制下跟踪期望轨迹xd。

3.1 滑模控制器的设计

滑模控制方法为含有不确定性的非线性系统鲁棒控制提供了有效的控制设计方法，可以使系统输出直接跟踪期望轨迹。基于改进三元模型设计滑模控制器。首先，根据控制需求，定义滑模函数：

s=ce+e·（13）

e=xd-x

其中，e是气动软体驱动器活动端的实际位移与期望轨迹的偏差；xd是平滑的期望轨迹，其一、二阶导数均有界；c是正的增益。结合式（11）与式（13），求解滑模函数s关于时间的导数，可得

s·=ce·+e¨=c（x·d-x·）+（x¨d-x¨）=

x¨d-z1-z2PC-d+c（x·d-x·）（14）

选择等速趋近率，即

s·=-ηsgn（s）（15）

其中，η为正常数，由此，将控制律设计为

pC=z-12（ηsgn（s）+x¨d+ce·-z1-d）（16）

上式中，d是不确定的量， 采用传统的滑模控制方法通常需要较大的开关增益来克服d，以保证控制系统的稳定性，这给系统带来了较大的抖振。为解决这一问题，利用RBF神经网络对d进行估计。

3.2 RBF神经网络的设计

由于RBF神经网络具有万能逼近的特性，故式（16）中的集总扰动项d可以表述为

d=W*Th（a）+ε（17）

a=（e，e·）T" h（a）=（h1，h2，…，hi）T

其中，a为网络的输入；W*为网络的理想权值；ε为网络的逼近误差，因为RBF神经网络能以任意精度逼近任意连续函数，故逼近误差ε是有界的，满足|ε|lt;εm；h（a）为高斯基函数的输出，其中，i为网络隐含层节点个数，隐含层第j个节点的输出hj可表示为

hj=exp（‖a-cj‖2/（2b2））（18）

cj=（cj1，cj2）T

其中，b为网络的基宽参数；cj为隐含层第j个节点的中心向量。通过神经网络对集总扰动项d进行逼近，神经网络的输出即d的估计值d^，d^可表示为

d^=W^Th（a）（19）

其中，W^为网络的实际权值，则式（16）中所设计的控制器可以改写为

pC=z-12（ηsgn（s）+x¨d+ce·-z1-d^） （20）

将式（20）代入式（14）可得

s·=x¨d-z1-z2pC-d+ce·" =-（d-d^）-ηsgn（s）（21）

可令

d～=d-d^==W～Th（a）+ε（22）

W～=W*-W^

式中，W～为神经网络理想权值与实际权值之间的偏差。

为了分析系统的稳定性，构造以下Lyapunov函数：

V=s2/2+（γW～TW～）/2（23）

其中，γgt;0。由Lyapunov稳定性的条件可知，为了使系统状态达到滑模面，需要满足ss·≤0，由式（21）～式（23）可得V关于时间的导数：

V·=ss·+γW～TW·～=

-W～T（s·h（a）+γW·^）-s（ε+ηsgn（s））（24）

为使V·lt;0，设计自适应律为

W·^=-1γs·h（a）（25）

则有

V·=-s（ε+ηsgn（s））=-sε-η|s|（26）

上式中，由于RBF神经网络能以任意精度逼近任意连续函数，故通过合理构建神经网络，可以使逼近误差ε为一个足够小的常数。此时，设置ηgt;ε可以保证V·lt;0。从式（26）中不难发现，当V·≡0时，有且仅有一种情况，即s≡0。因此，在控制器（式（20））和自适应律（式（25））的共同作用下，神经网络的权值会收敛于理想权值，滑模函数会收敛于滑模面s=0，进而使系统的状态收敛于目标状态。

4 实验与分析

基于实验数据辨识得到改进三元模型的参数，搭建控制器并设计三组实验来验证本文方法的有效性和优越性。

滑模控制方法［24］与PID控制方法［25］是当前常用的气动软体驱动器控制方法，三组实验中，将本文控制方法与传统滑模控制方法和PID控制方法进行对比，分别从正常运行情况下的固定幅频信号跟踪、负载质量存在明显不确定性情况下的固定幅频信号跟踪、变幅变频信号跟踪三个方面来验证本文方法的有效性和优越性。为了便于衡量参数辨识的效果以及对比控制性能的优劣，采用多个性能指标来对实验结果进行对比分析：均方根误差erms（root mean square error percentage， RMSEP）、最大误差emax（maximum error percentage， MEP）以及拟合度f（fitness），其计算公式分别为

erms=N-1∑Nj=1［xd（j）-x（j）］2max（xd）-min（xd）（27）

emax=max（|xd（j）-x（j）|）max（xd）-min（xd）（28）

f=1-∑Nj=1［xd（j）-x（j）］2∑Nj=1［xd（j）-x-d］2（29）

式中，x-d为目标信号xd的平均值。

4.1 模型的参数辨识

根据上文中对参数辨识方法及模型不确定性表示的分析，在0.20 Hz的输入压力频率下，负载为75 g、175 g、275 g、475 g、775 g时进行实验，采集驱动器活动端位移数据X与内部气压数据p，用于参数辨识。其中，将负载为75 g、175 g、275 g、475 g、775 g时采集的数据作为训练集，负载为475 g时采取的数据作为测试集。将训练集的四组数据整合后作为参数辨识的依赖数据。设模型参数初值θ0=（0，0，…，0），算法最高迭代次数为3000，准则函数梯度值下限为e-10，按照上文方法进行参数辨识。

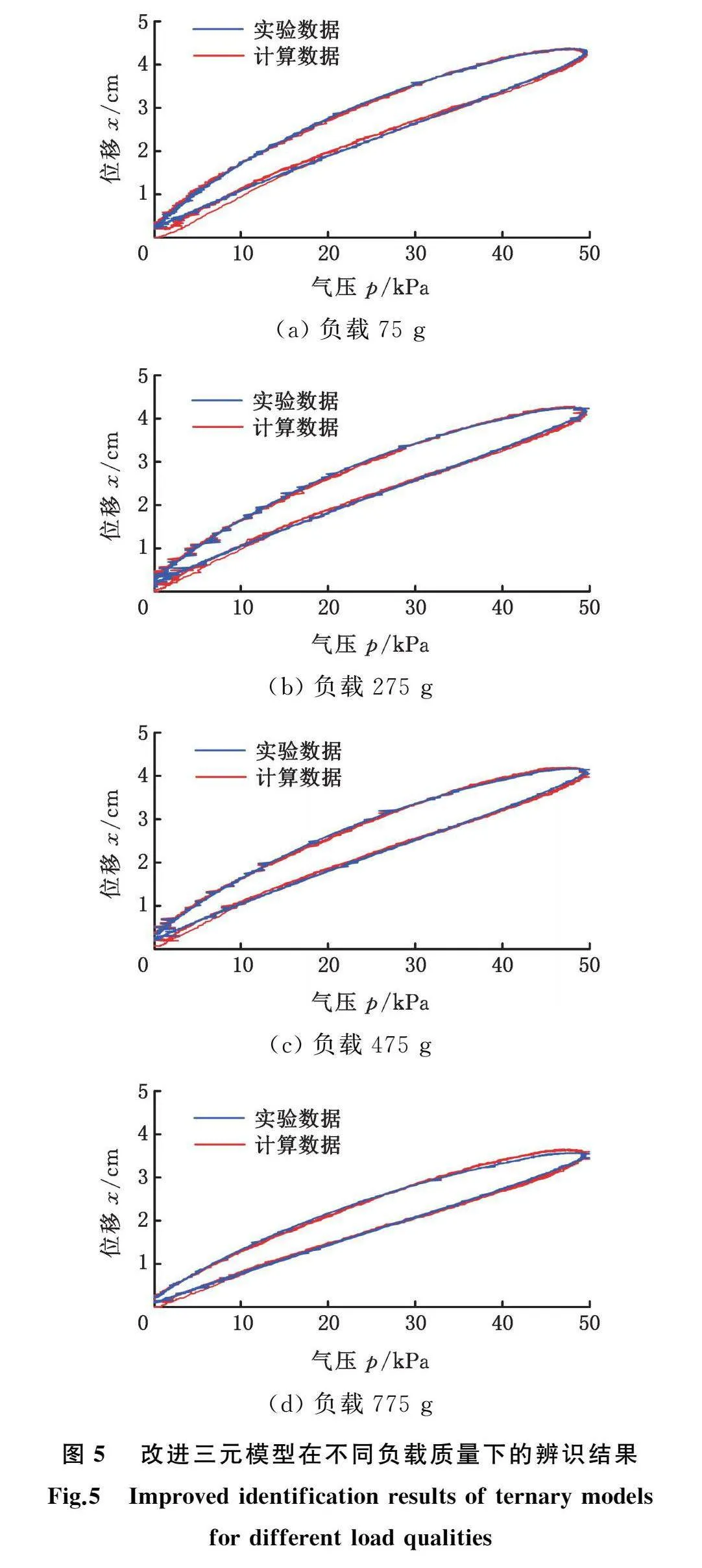
辨识获得的模型参数如下：B0=80.13，B1=531.61，K0=719.29，K1=597.27，F0=161.23，F1=9164.90，b0=77.89，b1=308.26，b2=-80.14。获得这些参数后，基于改进三元模型，依据内部气压数据集P以及负载质量M求取驱动器活动端位移的计算数据集Xk，将其与采集的实验数据集X进行比较，可以分析参数辨识的效果。训练集实验数据集X与计算数据集Xk的图形化比较如图5所示。

计算可得，当负载为75 g、175 g、275 g、775 g时，实验数据与计算数据间的均方根误差erms分别为1.53%、1.33%、1.27%、1.36%，由此可知，所提的改进三元模型能够在不同负载下较好地描述波纹管型气动软体驱动器的动力学特性。然后，利用测试集数据验证改进三元模型的泛化能力，图形化比较如图6所示。测试集实验数据与计算数据间的erms为1.32%，由此可知，虽然测试集数据没有作为参数辨识的依赖数据，但仍然可以利用改进三元模型较为精确地描述475 g负载下波纹管型气动软体驱动器的动力学特性，结果表明，改进三元模型具有良好的泛化能力。

4.2 控制器的建立

应用上文中获取的模型参数，可根据控制律（式（16））建立基于改进三元模型的滑模控制器。经由实验调试获取一组能够实现稳定控制且使得抖振较小的增益参数，即η=350、c=40（由于获得的模型参数值普遍较大，这些增益参数在控制器中相对于z1、z2依旧是很小的值）。

本文所提方案在上述滑模控制器的基础上采用RBF神经网络对系统集总误差进行逼近。根据控制律（式（20））建立基于改进三元模型的神经网络滑模控制器。RBF神经网络采取2-5-1结构，网络的初始权值取0，基宽参数值取b=5.0，隐含层各神经元中心向量值取c1=（-1，-1），c2=（-0.5，-0.5），c3=（0，0），c4=（0.5，0.5），c5=（1，1）。此外，通过实验分析，建立用于对照的PID控制器，其结构如下：

Pr=KPe+KI∫t0edt+KDe·（30）

其中，KP、KI、KD分别为PID控制器的比例系数、积分系数和微分系数。本文通过多次调试，取得了一组在当前实验平台控制效果最优的PID参数：KP=0.23，KI=2.00，KD=0.0015。

4.3 固定幅频期望轨迹跟踪

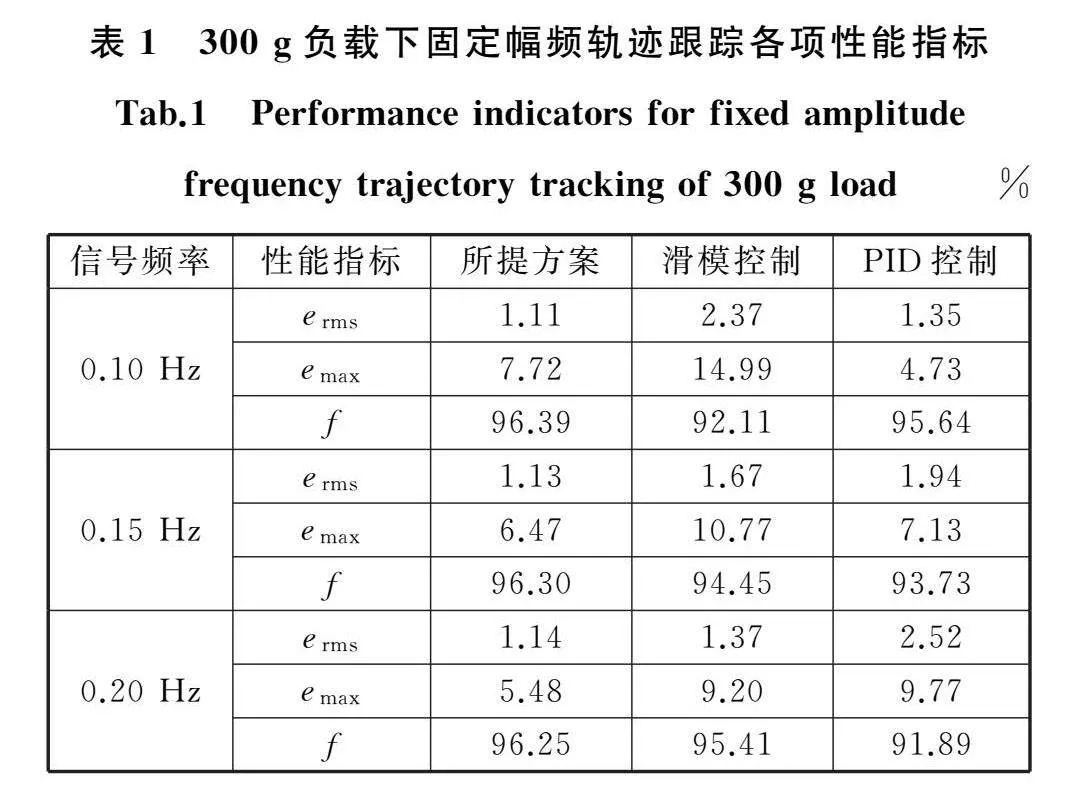
测试所提控制方法在正常运行（固定幅频信号输入，无明显外加干扰）情况下的控制性能。将实际系统的负载质量调为300 g，使模型中负载质量的标称值与实际值一致。分别在0.10 Hz、0.15 Hz、0.20 Hz三种固定频率的输入信号下使用传统滑模控制方法、PID控制方法与本文方法进行轨迹跟踪实验，记录相关数据。实验结果如图7所示。

三种控制方案的性能指标数据见表1。由图7及表1数据可知，在无明显外加干扰的情况下，三种控制方案均能够实现对于固定幅频输入信号的稳定跟踪。在三组实验中，所提方法的均方根误差被限制在1.10%～1.15%范围内，明显小于传统滑模控制方法的1.3%～2.4%以及 PID控制方法的1.3%～2.6%；所提方法的拟合度则处于96.25%～96.40%，同样优于传统滑模控制方法的92.10%～95.41%与PID控制方法的91.89～95.64%；所提方案的最大误差为5.48%～7.72%，全面低于传统滑模控制器的对应数据，与PID控制器的对应数据相近。该实验证明了所提方法在无外部扰动的运行情况下整体上有着高于传统滑模控制方法与PID控制方法的轨迹跟踪控制精度。

4.4 变幅变频期望轨迹跟踪

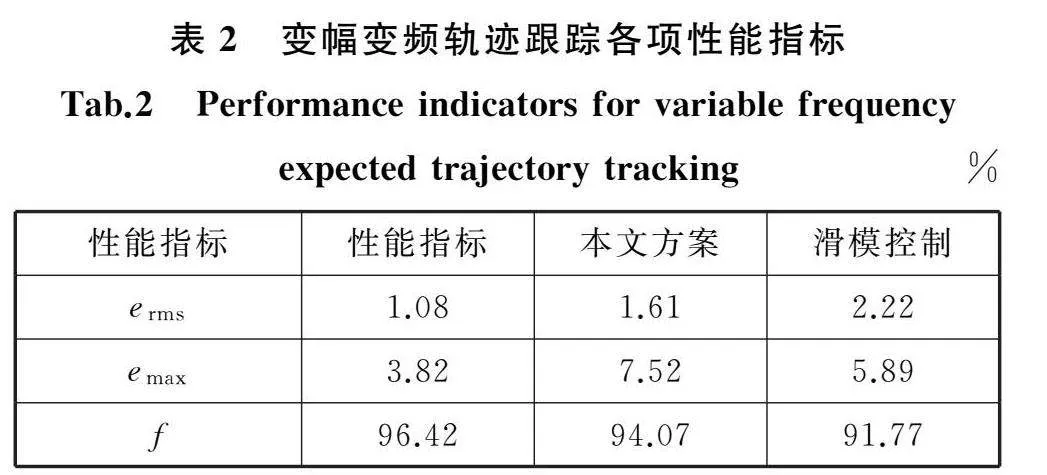
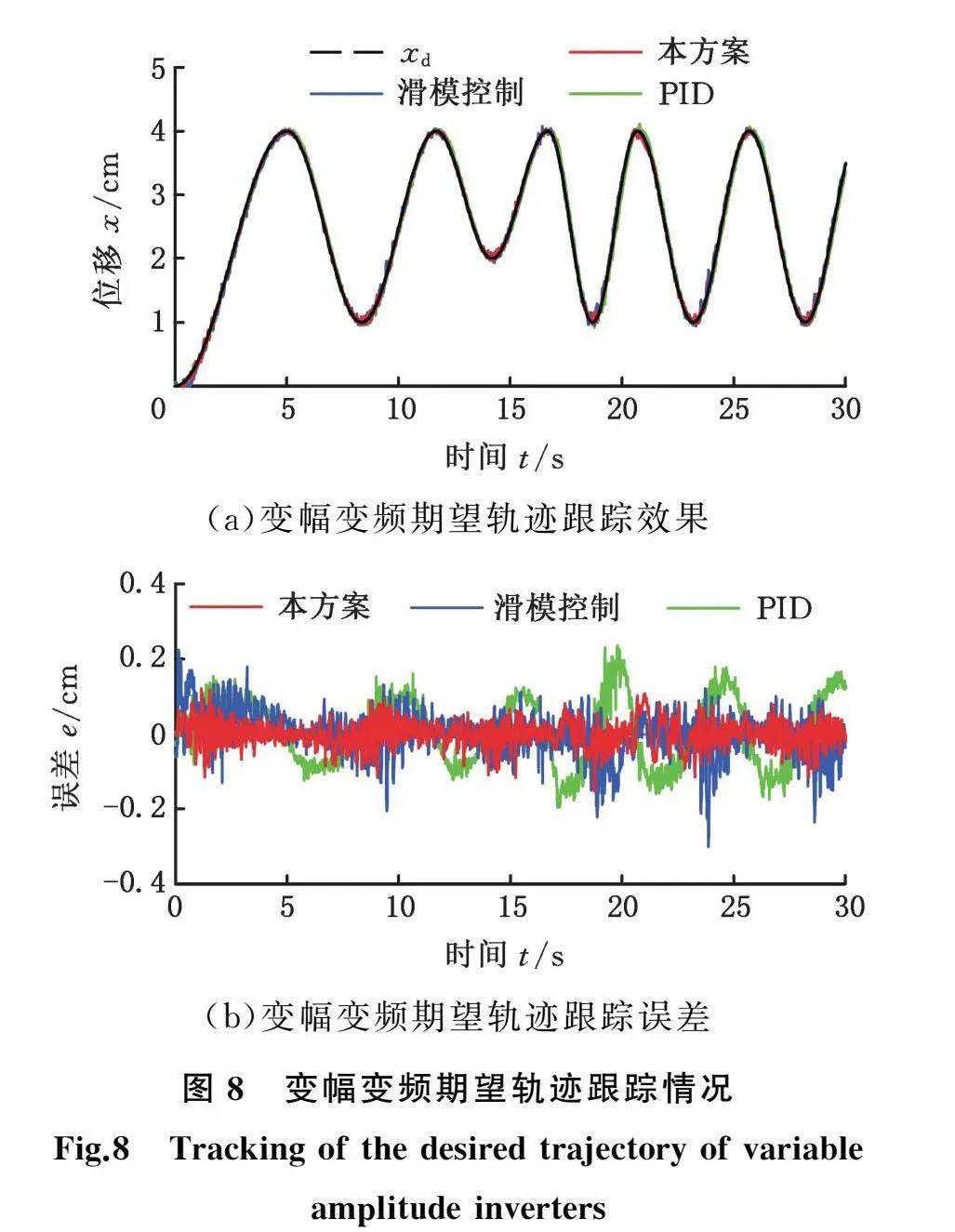
测试所提控制方法应对变幅变频输入信号的能力。将实际系统负载设置质量为300 g，使模型中负载质量的标称值与实际值一致，并保证控制器参数不变。输入信号采用一组幅值、频率随时间变化的的正弦波信号，使用传统滑模控制方法、PID控制方法与所提方法进行轨迹跟踪实验，记录相关数据。实验结果如图8所示。

三种控制方案的性能指标数据见表2。由图8及表2可知，三种控制方案均可实现对变幅变频期望轨迹的跟踪，其控制精度相较于跟踪固定幅频信号时未产生明显变化。所提方法在跟踪变幅变频信号时，均方根误差为1.08%，最大误差为3.82%，拟合度为96.42%，均优于传统滑模控制方法与PID控制方法的对应数据。该实验证明了所提方法能够较精确地跟踪变幅变频期望轨迹，且性能相较于传统滑模控制方法与PID控制方法更优。

4.5 载荷质量存在较大误差的期望轨迹跟踪

测试所提控制方法应对负载质量不确定性的能力，将驱动器的实际负载质量增大为350 g，但不改变控制器中有关负载质量的参数（标称负载质量仍为300 g），同样在0.10 Hz、0.15 Hz、0.20 Hz三种固定频率的输入信号下使用三种控制方法进行实验，记录相关数据，实验结果如图9所示。

三种控制方案的性能指标数据见表3。由图9及表3可知，由于实际载荷质量与模型参数产生了较大误差，高度依赖于系统模型的传统滑模控制方法的控制性能出现了明显下跌，相应实验数据中均方根误差与最大误差均有大幅度上升，而拟合度明显下降；而PID控制方法并不依赖于系统模型，其控制效果未受到明显影响；所提方法尽管同样依赖于模型，但RBF神经网络的作用较好地拟合了系统误差，使得控制精度保持在较高水平，均方根误差保持在1%～1.2%，拟合度保持在96%以上，最大误差也未出现明显变化，整体性能依旧明显优于传统滑模控制方法与PID控制方法。该实验证明了所提方法对于驱动器所带负载质量的不确定性具有良好的抗扰动能力。

5 结论

（1）本文建立了可以准确描述波纹管型气动软体驱动器运动特性的模型，并在此基础上设计控制器，实现了该驱动器的轨迹跟踪控制。

（2）本文对传统的三元模型进行了改进，考虑负载质量对于软体驱动器性能的影响，所建立的改进三元模型能够更好地描述波纹管型气动软体驱动器的动态特性，精确度更高。

（3）本文设计了一种RBF神经网络误差补偿器来对系统的不确定性进行估计和补偿，提出了一种滑模控制方法，在实现系统跟踪控制的同时克服了RBF神经网络的估计误差，具有较好的鲁棒性。

需要注意的是，本文所提的改进型三元模型是在传统三元模型基础上的改进，它和传统三元模型一样具有较好的普适性，可以应用于不同软体驱动器的建模中。未来将对本文所提方案进行进一步的优化与改进，如研究模型的在线参数辨识方法以减少前期采集数据的操作等。此外，还期望能够基于该软体驱动器搭建气动软体机器人，并将本文方法应用于气动软体机器人的控制中。

参考文献：

［1］ ASHURI T， ARMANI A， JALILZADEH HAMIDI R， et al. Biomedical Soft Robots：Current Status and Perspective［J］. Biomedical Engineering Letters， 2020， 10（3）：369-385.

［2］ RUS D， TOLLEY M T. Design， Fabrication and Control of Soft Robots［J］. Nature， 2015， 521：467-475.

［3］ 郭钟华， 吉成浩， 窦梦宇， 等. 轻韧型软体夹持器的仿生设计与研究［J］. 中国机械工程， 2023， 34（5）：595-602.

GUO Zhonghua， JI Chenghao， DOU Mengyu， et al. Bio-inspired Design and Research on Light Ductile Soft Grippers［J］. China Mechanical Engineering， 2023， 34（5）：595-602.

［4］ 张立彬， 鲍官军， 杨庆华， 等. 气动柔性球关节的模糊PID控制［J］. 中国机械工程， 2005， 16（5）：407-409.

ZHANG Libin， BAO Guanjun， YANG Qinghua， et al. Fuzzy-PID Control for Flexible Pneumatic Spherical Joints［J］. China Mechanical Engineering， 2005， 16（5）：407-409.

［5］ TONDU B， IPPOLITO S， GUIOCHET J， et al. A Seven-degrees-of-freedom Robot-arm Driven by Pneumatic Artificial Muscles for Humanoid Robots［J］. International Journal of Robotics Research， 2005， 24（4）：257-274.

［6］ POLYGERINOS P， LYNE S， WANG Zheng， et al. Towards a Soft Pneumatic Glove for Hand Rehabilitation［C］∥2013 IEEE/RSJ International Conference on Intelligent Robots and Systems. Tokyo， 2013：1512-1517.

［7］ BROWN E， RODENBERG N， AMEND J， et al. Universal Robotic Gripper Based on the Jamming of Granular Material［J］. Proceedings of the National Academy of Sciences of the United States of America， 2010， 107（44）：18809-18814.

［8］ GAYLORD R H. Fluid Actuated Motor System and Stroking Device：US2844126［P］. 1958-07-22.

［9］ CAO Yu， HUANG Jian. Neural-network-based Nonlinear Model Predictive Tracking Control of a Pneumatic Muscle Actuator-driven Exoskeleton［J］. IEEE/CAA Journal of Automatica Sinica， 2020， 7（6）：1478-1488.

［10］ 谢胜龙， 李铁风， 王斌锐， 等. 基于KP模型的气动肌肉迟滞建模方法［J］. 中国机械工程， 2020， 31（10）：1183-1189.

XIE Shenglong， LI Tiefeng， WANG Binrui， et al. Hysteresis Modeling Method of Pneumatic Muscles Based on KP Model［J］. China Mechanical Engineering， 2020， 31（10）：1183-1189.

［11］ 赵苓， 李奇. 气动人工肌肉驱动单关节机械臂的自抗扰控制［J］. 液压与气动， 2017（3）：38-42.

ZHAO Ling， LI Qi. An Active Disturbance Rejection Control Approach for One-DOF Manipulator Driven by Pneumatic Artificial Muscles［J］. Chinese Hydraulics amp; Pneumatics， 2017（3）：38-42.

［12］ DMMER G， GABLENZ S， HILDEBRANDT A， et al. PolyJet-printed Bellows Actuators：Design， Structural Optimization， and Experimental Investigation［J］. Frontiers in Robotics and AI， 2019， 6：34.

［13］ DROTMAN D， ISHIDA M， JADHAV S， et al. Application-driven Design of Soft， 3-D Printed， Pneumatic Actuators with Bellows［J］. IEEE/ASME Transactions on Mechatronics， 2019， 24（1）：78-87.

［14］ HASHEM R， STOMMEL M， CHENG L K， et al. Design and Characterization of a Bellows-driven Soft Pneumatic Actuator［J］. IEEE/ASME Transactions on Mechatronics， 2021， 26（5）：2327-2338.

［15］ KHAN A H， LI Shuai. Sliding Mode Control with PID Sliding Surface for Active Vibration Damping of Pneumatically Actuated Soft Robots［J］. IEEE Access， 2997， 8：88793-88800.

［16］ 李光， 符浩. 无模型机械臂BP神经网络状态观测及反演跟踪控制［J］. 中国机械工程， 2016， 27（7）：859-865.

LI Guang， FU Hao. BP Neural Network State Observation and Backstepping Tracking Control of Model-free Robotic Manipulators［J］. China Mechanical Engineering， 2016， 27（7）：859-865.

［17］ WU Jun， HUANG Jian， WANG Yongji， et al. Fuzzy PID Control of a Wearable Rehabilitation Robotic Hand Driven by Pneumatic Muscles［C］∥2009 International Symposium on Micro-Nano Mechatronics and Human Science. St. Louis， 2009：408-413.

［18］ AHN K K， NGUYEN H T C. Intelligent Switching Control of a Pneumatic Muscle Robot Arm Using Learning Vector Quantization Neural Network［J］. Mechatronics， 2007， 17（4/5）：255-262.

［19］ 张启航， 邵敏， 任树雄， 等. 仿象鼻气动连续体机器人的运动学建模与运动控制［J］. 西安交通大学学报， 2021， 55（8）：25-32.

ZHANG Qihang， SHAO Min， REN Shuxiong， et al. Kinematic Modeling and Motion Control of a Pneumatic Trunk-type Continuum Robot［J］. Journal of Xi’an Jiaotong University， 2021， 55（8）：25-32.

［20］ YAN Hongwei， LI Hongbin， ZHOU Shengjun. LQR Optimal Control on the Positioning Accuracy and Rigidity for the Pneumatic Actuator［C］∥Proceedings of the 5th International Conference on Electrical Engineering and Automatic Control. Berlin， 2016：1097-1104.

［21］ 邢科新， 徐建明， 何德峰， 等. 气动肌肉的三元素模型辨识研究［J］. 高技术通讯， 2013， 23（5）：497-503.

XING Kexin， XU Jianming， HE Defeng， et al. Research on Identifying the Three-element Model for Pneumatic Muscle［J］. Chinese High Technology Letters， 2013， 23（5）：497-503.

［22］ REYNOLDS D B， REPPERGER D W， PHILLIPS C A， et al. Modeling the Dynamic Characteristics of Pneumatic Muscle［J］. Annals of Biomedical Engineering， 2003， 31（3）：310-317.

［23］ ZHAO Shiying， YAN Ze， MENG Qingxin， et al. Modified Three-element Modeling and Robust Tracking Control for a Planar Pneumatic Soft Actuator［J］. IEEE Transactions on Industrial Electronics， 2023， 70（9）：9237-9247.

［24］ HUMAIDI A J， KADHIM S K， SADIQ M E， et al. Design of Optimal Sliding Mode Control of Pam-actuated Hanging Mass［J］. ICIC Express Letters， 2022， 16（11）：1193-1204.

［25］ 田艳兵， 成中伟， 韩森. 高精密气动波纹管驱动伺服系统建模与仿真［J］. 液压与气动， 2015（9）：126-129.

TIAN Yanbing， CHENG Zhongwei， HAN Sen. The Modeling and Simulating of Servo System Driven by High Precision Pneumatic Bellows［J］. Chinese Hydraulics amp; Pneumatics， 2015（9）：126-129.

（编辑 陈 勇）