基于多智能体深度Q网络交互的板壳加强筋生长式设计

摘要：基于板壳加强筋生长步序列的马尔可夫性质，提出了板壳加强筋生长式设计的强化学习驱动策略。以结构整体应变能最小化为目标，运用马尔可夫决策过程对板壳加强筋的生长过程进行建模。通过引入多智能体系统，共享加强筋生长式过程的状态奖励并记忆特定动作，降低学习复杂度，实现了加强筋生长式过程奖励值的波动收敛，达成板壳加强筋生长式设计策略。最后给出算例并将平滑处理后的加强筋布局与经典算法的设计结果进行对比，验证了基于多智能体深度Q网络交互的板壳加强筋生长式设计的有效性。

关键词：板壳加强筋；生长式；多智能体深度Q网络；布局设计；强化学习

中图分类号：TH11;TP31

DOI：10.3969/j.issn.1004132X.2024.08.008

开放科学（资源服务）标识码（OSID）：

Growth Design of Stiffeners for Shell/Plate Structures Based on

MADQN Interaction

ZHONG Yi YANG Yong JIANG Xuetao PAN Shunyang ZHU Qixin WANG Lei

College of Mechanical Engineering，Suzhou University of Science and Technology，Suzhou，Jiangsu，215009

Abstract： Based on the Markov property of the growth steps of shell/plate stiffeners， a reinforcement learning driving strategy of the growth design of shell/plate stiffeners was proposed. Aiming at minimizing the overall strain energy of the structures， Markov decision process was used to model the growth processes of the stiffeners. By introducing a multi-agent system to share the states and the rewards of the stiffeners growth processes， and memorizing specific actions， the learning complexity was reduced. Meanwhile， the convergence of the reward value of the stiffeners growth processes was realized. Therefore， the growth design strategy of shell/plate stiffeners was achieved. Finally， a numerical example was given and the results of the smoothed stiffeners layout were compared with those of the classical algorithm， which verifies the validity of the growth design of stiffeners for shell / plate structures based on MADQN interaction.

Key words： stiffener for shell/plate structure; growth pattern; multi-agent deep Q network（MADQN）; layout design; reinforcement learning

0 引言

板壳结构在船舶、汽车、航空航天等领域具有极其广泛的应用，在板壳结构表面设计加强筋，能够在保证轻量化的同时显著提高结构的刚度等力学性能。板壳加强筋的设计主要包括加强筋的位置、尺寸和形状设计。在工程实际中，加强筋布局的确定很大程度上依赖于工程经验，如何同时保证加强筋结构的轻量化和承载性，一直是板壳加强筋设计领域的难点和重点。

板壳加强筋布局设计领域常用的方法为拓扑优化方法，这类方法通过将加强筋的布局问题转化为材料的分布问题来实现加强筋布局的优化。常用于板壳加强筋布局设计问题的拓扑优化技术包括均匀化法、变密度法、渐进结构优化法（evolutionary structural optimization，ESO）等。MA等［1］提出了一种基于均匀化方法的加固板生成设计方法，优化了基于等效模型的加固布局。WANG等［2］将渐进式均匀化方法引入分层加筋板的屈曲分析和优化问题的求解中。在变密度法中，最具代表性的模型是BENDS E等［3］提出的固体各向同性惩罚材料（solid isotropic material with penalization，SIMP）模型。LI 等［4］将变密度法（SIMP）与相场法相结合，对复合材料结构的抗断裂性进行优化研究。然而，基于SIMP法框架得到的优化结果存在大量的灰度单元，无法获得清晰的加强筋布局。LI等［5］将进化算法转换为数学模型，对加强筋自适应生长过程进行建模并结合所提出的“刚度变换方法”，使得加强筋能够朝着任意方向生长。

上述通过将加强筋的布置问题转化为材料的分布问题来进行设计的方法，得到的只是加强区域的分布，而不是具体的加强筋结构，这导致需要后处理才能确定加强筋的分布与尺寸，增加了实际工程设计的难度。随着研究的进一步深入，其他方法也被尝试应用到加强筋的布局设计中。如FATEMI等［6］以加强筋的位置为设计变量，利用直线来描述加强筋并结合遗传算法对直线的坐标参数进行优化，最终得到了清晰的加强筋布局。MULANI等［7］用B样条曲线来描述加强筋，利用粒子群算法对曲线的特征点坐标进行优化，最终实现了曲线加强筋的布局优化设计。然而这类采用遗传算法或粒子群优化算法对直线端点和B样条控制点进行优化从而实现加强筋的布局设计的方法仍然难以解决多载荷复杂工况下的加强筋设计问题。张卫红等［8］以结构最大刚度为目标，提出了几何背景网格法，实现了加筋设计域内任意离散网格沿加筋高度方向的布局参数化定义和三维曲面薄壁壳结构的加筋布局设计。ZHANG等［9］基于移动可变形组件法求解了三维结构加强筋的拓扑优化问题，成功避免了灰度单元，但是采用实体单元进行有限元计算仍然存在庞大的计算量。崔荣华等［10］引入水平集方法对加强筋布局进行描述并用不同的抗弯刚度表征薄板与加强筋，成功避免了灰度单元，获得了清晰的加强筋布局与尺寸。但是水平集方法在应用中还存在许多不足，如收敛速度慢、数值计算复杂（尤其是三维问题）、优化结果严重依赖孔洞的初始布置等。DING等［11］将自然界分支系统的自适应生长规律应用于板壳加强筋分布设计方法的研究，并提出了自适应成长法。LI等［12］和薛开等［13］根据双子叶植物叶脉形成的结构力学规律和形态发生的结构力学假说，提出脉序生长法（venation growth algorithm， VGA）。SHEN等［14］将附加调谐质量阻尼器的最佳调谐引入自适应成长法的求解中，以提高受谐波激励的3D箱体结构的结构动力学性能。张坤鹏等［15］采用结构参数特征图像化表征的方法对含曲筋布局的开口多级加筋壁板进行优化设计。董伟等［16］利用均匀化方法计算点阵结构的宏观性能，实现了点阵加筋板式结构布局的优化设计。SINGH等［17］提出将深度神经网络（deep neural networks，DNNs）与MSC NASTRAN计算相结合以近似表示FEA屈曲响应，展现了基于DNN的机器学习算法在加速曲线型加强板优化方面的潜力。LIU等［18］提出了一种基于深度学习的智能优化框架，用于网格加固面板的加强筋单元格优化设计。

为了避免对梯度信息和先验知识的依赖性，降低设计难度并实现清晰的加强筋布局设计，本文基于板壳加强筋生长步序列的马尔可夫性质，提出板壳加强筋生长式设计的强化学习驱动策略。以最小化结构整体应变能为优化目标，运用马尔可夫决策过程对板壳加强筋生长过程进行建模。通过多智能体深度Q网络（multi-agent deep Q network， MADQN）与加强筋生长环境的交互，实现加强筋生长过程奖励值的上升与波动收敛，达成板壳加强筋生长式设计。最后给出算例，并将平滑处理后的加强筋布局与经典算法的结果进行对比，验证基于多智能体深度Q网络交互的板壳加强筋生长式设计的有效性。

1 板壳加强筋生长式设计模型的构建

根据自然界植物分支系统的形态形成机理，植物叶脉在不同的环境中具有自适应性，这在很大程度上增强了植物整体的力学性能。 脉序生长算法［13］以变形能和剪应力为生长规则分别指导加强筋生长脉络的生长，其根本原理是自然界植物叶脉系统依据一定的生长规律并通过生长过程最终达到整体性能最优。本文将这种结构生长式机理应用于板壳加强筋设计中，即加强筋脉络的生长总是以优化目标为导向，朝着提升结构性能更显著的方向生长，下面构建生长式设计模型。

板壳加强筋生长式设计的约束函数为加强筋的体积上限，优化目标为结构的整体刚度最大化，即结构整体柔顺度最小化。根据结构的应变能和柔顺度的一致性，优化目标等价于结构整体应变能最小化。优化目标及约束函数的数学模型可表示为

min U

s.t. Vs≤Vs.max

式中，U为结构整体应变能；Vs、Vs.max分别为加强筋体积及其上限。

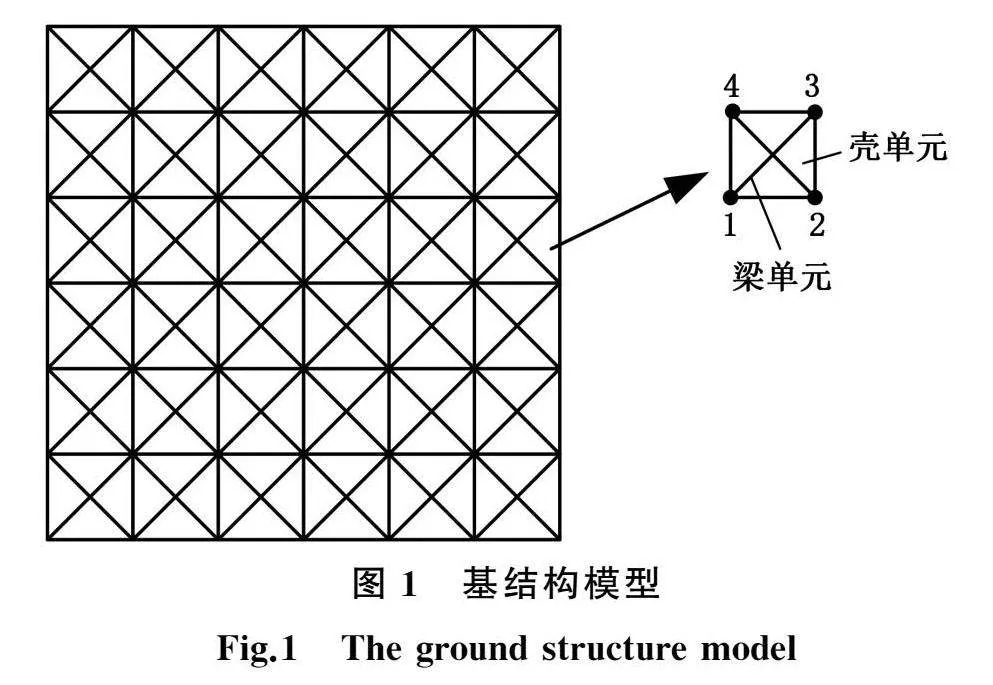
板壳加强筋生长式设计的有限元几何模型采用基结构法构建，基结构模型如图1所示。采用四节点四边形单元离散板壳结构，创建梁单元连接壳单元相关节点作为加强筋，梁单元截面类型为正方形，加强筋单面加筋的布置方式，加强筋截面尺寸及布置方式如图2所示，即加强筋的截面形心位于壳结构的一侧。

板壳加强筋生长式设计方法的具体生长准则如下：

（1）采用Abaqus/CAE对薄板加强筋模型进行参数化设计。采用忽略横向剪切变形的基尔霍夫板来模拟基板的变形情况，采用四节点壳单元构建基础模型，两节点梁单元构建加强筋，梁单元横截面采用正方形截面，且截面尺寸固定。

（2）在板壳加强筋生长式设计过程中，以加筋结构整体应变能最小为优化目标，加强筋体积上限为约束条件。文献［11，19］中对具有相同载荷和支撑的算例布置不同位置的“种子”，并进一步对添加加强筋后结构的力学性能进行对比，得出结论如下：加强筋生长“种子”应该位于结构的载荷点、支撑点或边缘。根据结构的承载条件并依据文献［11，19］的种子选取原则，选择约束和载荷作用区域布置种子。

（3）根据脉序生长算法所提出的生长机理［13］，对加强筋脉络的生长准则进行本文方法适应性的修改，即规定在加强筋的生长过程中仅存在以应变能最小为生长原则的主脉，而不存在次脉；仅存在单支生长，而不存在分支、退化等情况。

在板壳加强筋生长式设计过程中，下一状态的加强筋生长布局仅与当前的加强筋生长布局以及加强筋下一生长步的生长方向相关，可以看出加强筋生长步是一组满足马尔可夫性质的随机变量序列，加强筋生长过程呈现典型马尔可夫性质：当给定当前状态时，未来的状态与过去的状态是条件独立的。因此，在板壳加强筋生长式设计模型构建的基础上，运用马尔可夫决策过程进一步构建板壳加强筋生长式设计的强化学习驱动策略。

2 板壳加强筋生长环境交互的多智能体深度Q网络

2.1 搭建板壳加强筋生长环境与智能体交互模型

强化学习（reinforcement learning， RL）是机器学习中重要的一部分。强化学习由环境和智能体两部分组成，通过环境与智能体的交互获得奖励或惩罚，通过不断地在交互式环境中进行探索利用（exploration-exploitation）的权衡来学习一系列动作，进而使预期回报最大化。

在板壳加强筋生长式设计中，首先构建板壳加强筋生长环境与智能体交互机制：在强化学习的训练过程中，智能体与板壳加强筋生长环境不断进行交互，如图3所示。板壳加强筋生长环境将当前加强筋生长状态与奖励传递给智能体，智能体根据当前加强筋生长状态选择下一加强筋生长方向，并将所选择的下一加强筋生长方向返回板壳加强筋生长环境，板壳加强筋生长环境得到智能体选择的下一加强筋生长方向后，执行加强筋生长的动作并进入加强筋生长的下一个状态，随后将加强筋生长的下一状态和奖励传递给智能体，这种交互过程可以用马尔可夫决策过程表示。

2.2 构建加强筋生长式设计的马尔可夫决策过程

在马尔可夫决策过程中，可以用p（st+1=s′|st=s，at=a）来表示状态转移，即在训练步数为t时环境状态为s，在状态s选择动作a，会转移到状态s′，未来的状态st+1由当前的状态st和当前智能体采取的动作at共同决定。状态转移是具有马尔可夫性质的。

随机变量R0，R1，…，RT构成一个加强筋随机生长过程，其中，T表示训练次数。随机变量的取值空间的集合称为状态空间，Rt+1对过去状态的条件概率分布可以仅用Rt的函数表示为

p（Rt+1=rt+1|R0∶t=r0∶t）=

p（Rt+1=rt+1|Rt=rt+1）

式中，R0∶t为变量集合，即板壳加强筋历史生长布局的集合{R0，R1，…，RT}；r0∶t为状态空间中的状态序列，即加强筋生长步序列r0，r1，…，rt。

板壳加强筋生长步的马尔可夫决策过程满足以下条件：

p（st+1|st，at）=p（st+1|ht，at）

其中，集合ht={s1，s2，…，st}包含之前所有的加强筋生长步状态，是加强筋生长步状态的历史。s1，s2，…，st是一组具有马尔可夫性质的随机变量序列。

2.3 加强筋生长式设计的多智能体深度Q网络模型的构建

深度Q网络（deep Q network， DQN）通过使用非线性神经网络近似Q函数。神经网络用θ进行参数化表示并以最小化损失函数为目标函数：

L（θ）=E［（r+γmax Q（s′，a′;θ′）-Q（s，a;θ））2］

式中，s为状态；a为动作；r为奖励；s′为下一状态；a′为下一动作；［r+γmax Q（s′，a′;θ′）］为目标网络（target network）输出的Q值，包含获得的奖励、下一状态价值的估计两部分；Q（s，a;θ）为Q值的当前估计。

深度Q网络能够在与环境的交互学习中最小化预测网络输出的Q值（Q值的当前估计）与目标网络输出的Q值（Q值的更新估计）之间的差异，从而达到能够输出符合预期目标的动作策略并且使奖励上升与波动收敛的学习目的。

在板壳加强筋生长式设计过程中，加强筋生长“种子”的位置和数量根据工况的不同而有差异，并且“种子”数量的增加显著提高了DQN智能体权衡探索利用的成本与难度。为了解决这一问题，本方法在采用DQN的基础上引入多智能体系统（multi-agent deep reinforcement learning， MADRL），n个智能体与n个“种子”相对应，多个智能体之间具有共享的状态和奖励，并在经验回放池中进行每个智能体特定的动作更新，在多智能体与板壳加强筋生长式环境的交互学习过程中实现预期目标。

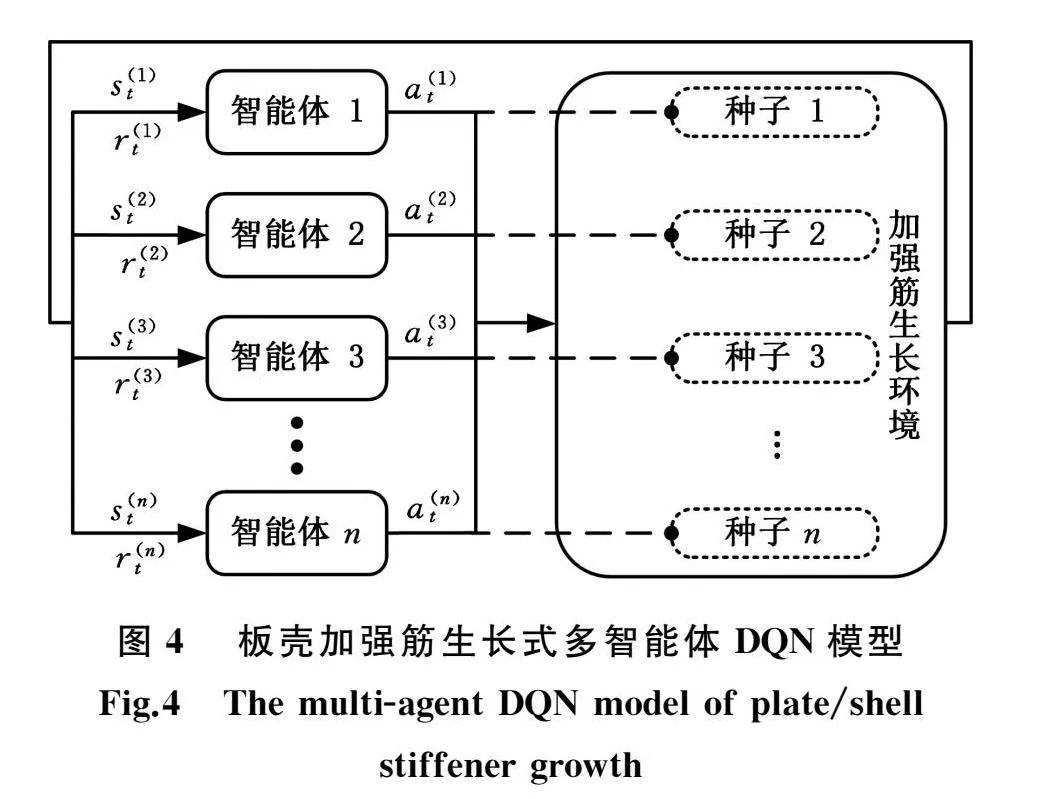
在基于多智能体深度Q网络交互的板壳加强筋生长式设计中，板壳加强筋生长式过程用动作、状态和奖励描述。如图4所示，在训练次数为t时，获得环境状态s（n）t的智能体An根据策略选择动作a（n）t并控制“种子”n生长，当所有种子的动作被执行后，环境依据状态转移概率转移到下一时刻的状态s（n）t+1，同时，每个智能体An得到执行动作a（n）t后的奖励r（n）t。

3 板壳加强筋生长式多智能体深度Q网络的算法设计

3.1 加强筋生长过程的状态动作空间设计

在板壳加强筋生长式多智能体深度Q网络交互环境中，智能体An能够在t时刻观测到种子n相关的环境状态s（n）t：

s（n）t={Seed_label（n）t，ΔSE（n）t，ΔMASS（n）t}

式中，Seed_label（n）t为当前状态加强筋生长起点的网格节点号；ΔSE（n）t为当前状态结构整体应变能与上一状态应变能差值；ΔMASS（n）t为当前状态结构整体质量与上一状态质量的差值。

建模过程中加强筋用两节点梁表示，加强筋生长的动作空间为以生长起点为中心的8个生长角度0°、45°、90°、135°、180°、225°、270°、315°，加强筋从生长起点（上一状态加强筋的生长终点）开始生长，从8个生长角度中选择生长方向生长直至此次加强筋生长终点。采取ε-贪心策略，ε为一个很小的值，以ε的小概率随机选择动作空间内的动作，以1-ε的概率选择预测Q值最大的动作a，探索分布为

πQ（st）=argmaxa Q（st，a）" 1/Tθslt;Pelt;1

arandom0≤Pe≤1/Tθs

其中，Pe为随机生成的概率；Ts为训练次数，用1/Tθs表示ε，随着训练次数的增加而递减，0lt;θlt;1为控制1/Tθs大小的参数，以调节智能体选择随机动作进行探索或利用的概率。

3.2 加强筋生长过程的奖励函数设计

奖励函数是引导智能体学习的关键性因素，通过对智能体采取的策略进行评价并将相应奖励或惩罚反馈给智能体，从而引导智能体在复杂多维的环境中学习到符合目标导向的决策。在本文方法中，目标函数为加筋板壳结构整体应变能的最小化，因此选择结构整体应变能变化量ΔSE作为自变量构建奖励函数。同时，由于位于板壳顶点或边界等特殊位置的节点作为加强筋的生长起点时存在某些角度无法生长的情况，故设置惩罚因子作为负奖励。最终得到奖励函数：

r=rneg" ""Seed_label（n）t=Seed_label（n）t-1

x1ΔSE其他

式中，rneg为负奖励；x1为系数，用以调节ΔSE的大小，从而降低奖励值的方差，保证训练过程中梯度更新的稳定性。

4 典型算例

为便于验证所提方法的正确性，选取研究领域内常用的共识性典型算例，采用多智能体深度Q网络模型进行加强筋生长式设计。奖励值波动收敛后，对加强筋初步设计结果进行平滑处理，最终得到加强筋生长式设计结果，并将本文方法得到的设计结果与文献［6］中经典算法的设计结果进行对比。

文献［6］采用遗传算法，通过对梁式加强筋两端的坐标进行参数化表征与优化实现加强筋的设计。此方法允许加强筋在板壳单元内任意放置，能够得到清晰流畅的加强筋布局。但该方法存在以下不足：①需要对加强筋进行参数化描述及复杂的计算，工作量与难度随着工况的复杂和加强筋数量的增加而急剧增大;②难以对需要加强筋进行密集分布才能提高刚度性能的问题进行有效求解。针对上述问题，本文提出板壳加强筋生长式设计的强化学习驱动策略，克服了对梯度信息与先验知识的依赖性，大大降低了设计难度，该方式可以有效解决某些特定区域需要加强筋密集生长才能达到的刚度强化需求。

4.1 角点固支方板

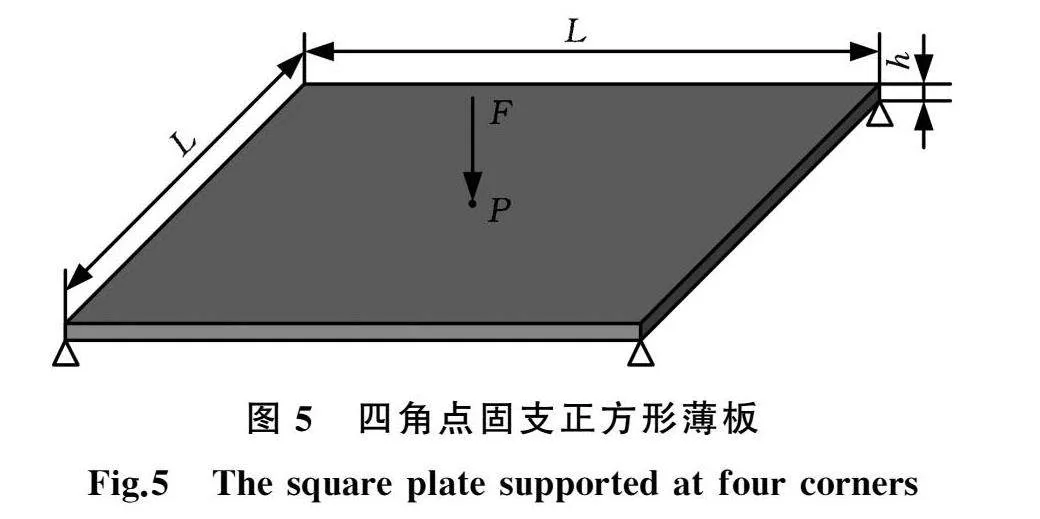
算例1为四角点固支的正方形薄板［6，11］，如图5所示。中心P点受集中载荷F=200 N。基板长、宽均为0.2 m，厚度为3 mm，加强筋截面形状为正方形，边长为3 mm。材料弹性模量E=69 GPa，泊松比为0.33，加筋材料用量不超过薄板体积的25.5%。

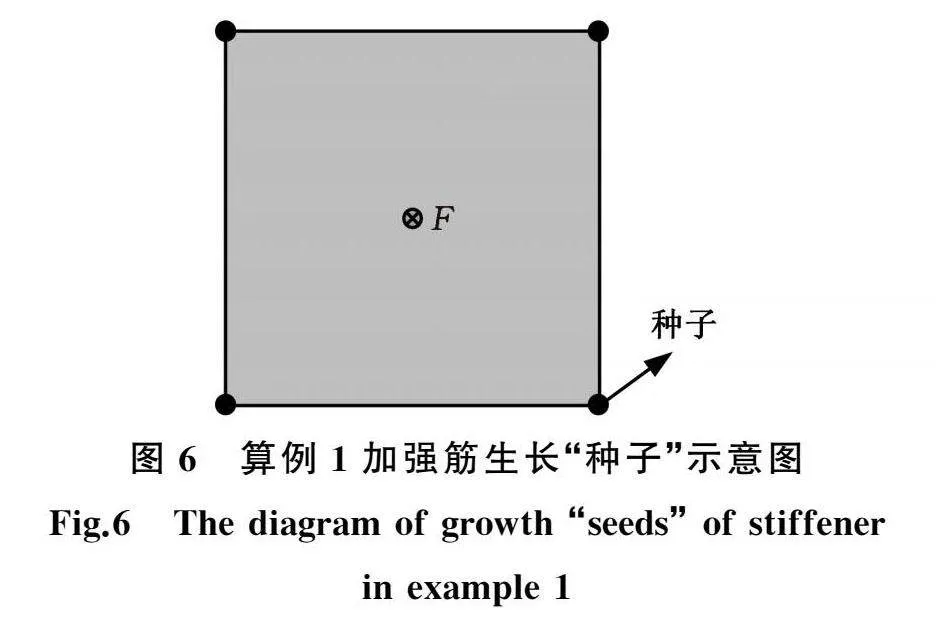
在本算例中，设置加强筋生长“种子”数量为4，分别位于正方形薄板固支的四个角点，如图6所示。在以应变能变化量为自变量的奖励函数的引导下，加强筋从“种子”开始依照智能体ε-贪心策略选择的方向生长。同时，DQN智能体不断与加强筋仿真建模环境交互并进行网络训练。加强筋训练奖励值与训练次数之间的关系如图7所示。由图7可知，训练奖励值具有上升并波动收敛的趋势，这说明随着训练次数的增加，加强筋愈发朝着能够减小更多应变能的方向生长，证明了所提出的基于多智能体深度Q网络交互的板壳加强筋生长式设计的有效性。

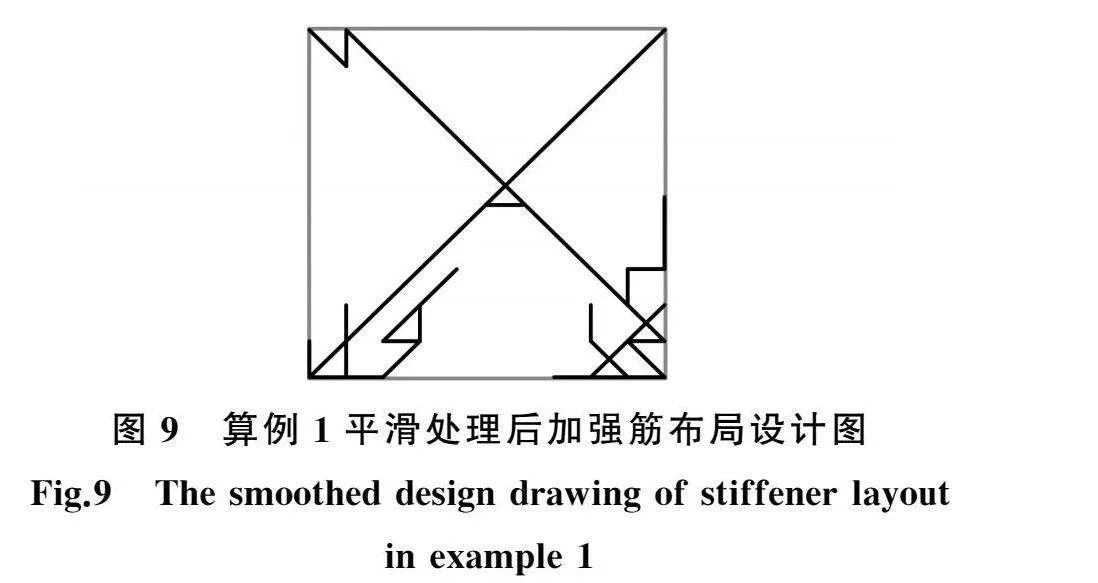
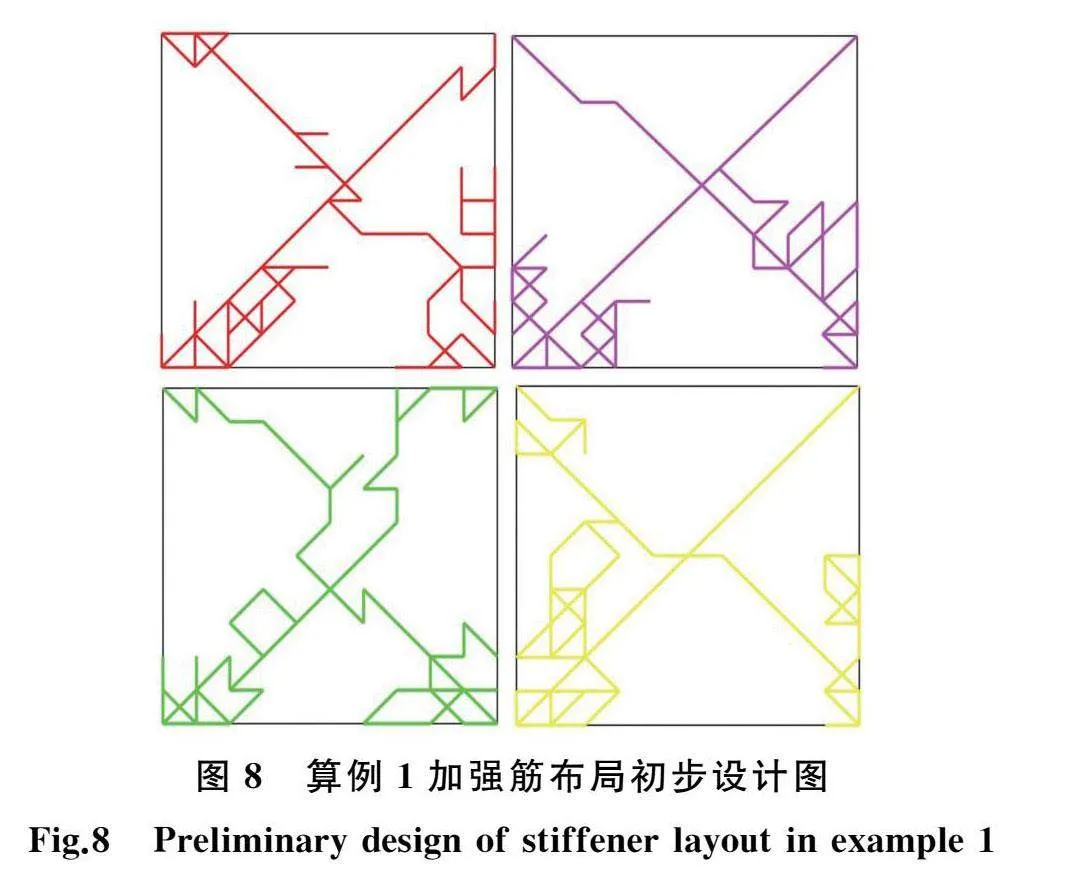
根据智能体训练情况，得到加强筋生长式设计的初步设计结果，如图8所示。然而，由于深度强化学习DQN模型是一种探索利用权衡的算法，ε-贪心策略具有采取的动作的不确定性和随机性，会影响加强筋生长路径的平滑性，故需要进一步地对初步得到的加强筋生长式布局进行平滑处理。将图8所示的四张加强筋初步设计图重叠，取重合的加强筋生长步，去除单独的加强筋生长步，最终得到平滑处理后的加强筋生长式设计图（图9）。文献［6］利用遗传算法进行加强筋布局设计，最终设计结果如图10所示。将最终得到的加强筋生长式设计结果与文献［6］得到的设计结果对比后可以看出，本文方法得到的设计结果与遗传算法得到的设计布局整体上一致，加强筋分布清晰合理，说明本文方法能够有效地解决加强筋生长式设计问题。以应变能数值表征刚度，加强筋三维设计图见图11，经仿真计算得出结论如下：加强筋材料体积增量为8.43%，结构整体应变能减小40.79%。

4.2 单边固支方板

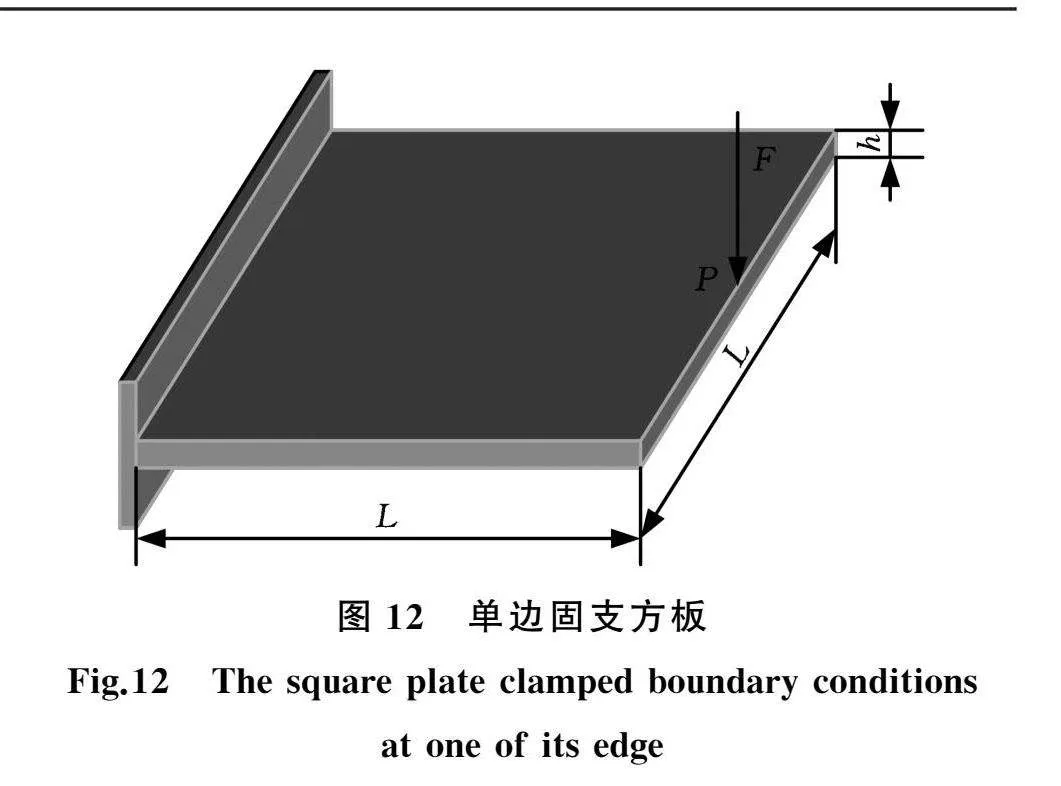
选取单边固支方板［6，20］作为另一个典型算例，其基本尺寸与算例1相同，包括薄板、加强筋的尺寸，集中载荷大小，材料的弹性模量、泊松比。其中，加筋材料用量不超过薄板体积的19.1%，载荷位于P点，如图12所示。

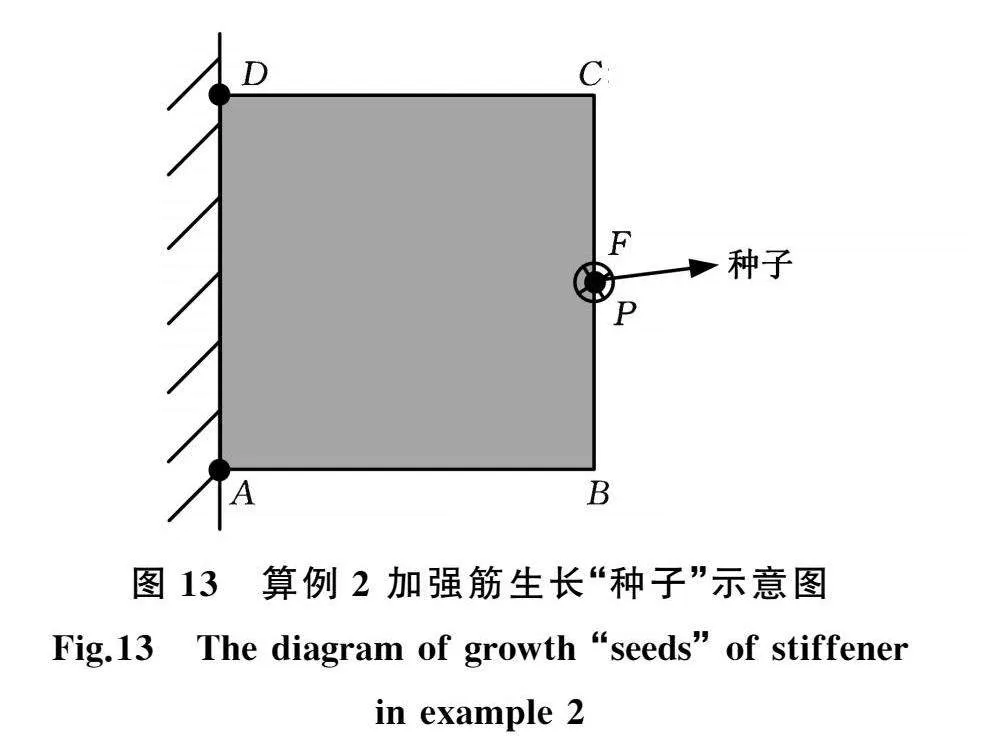
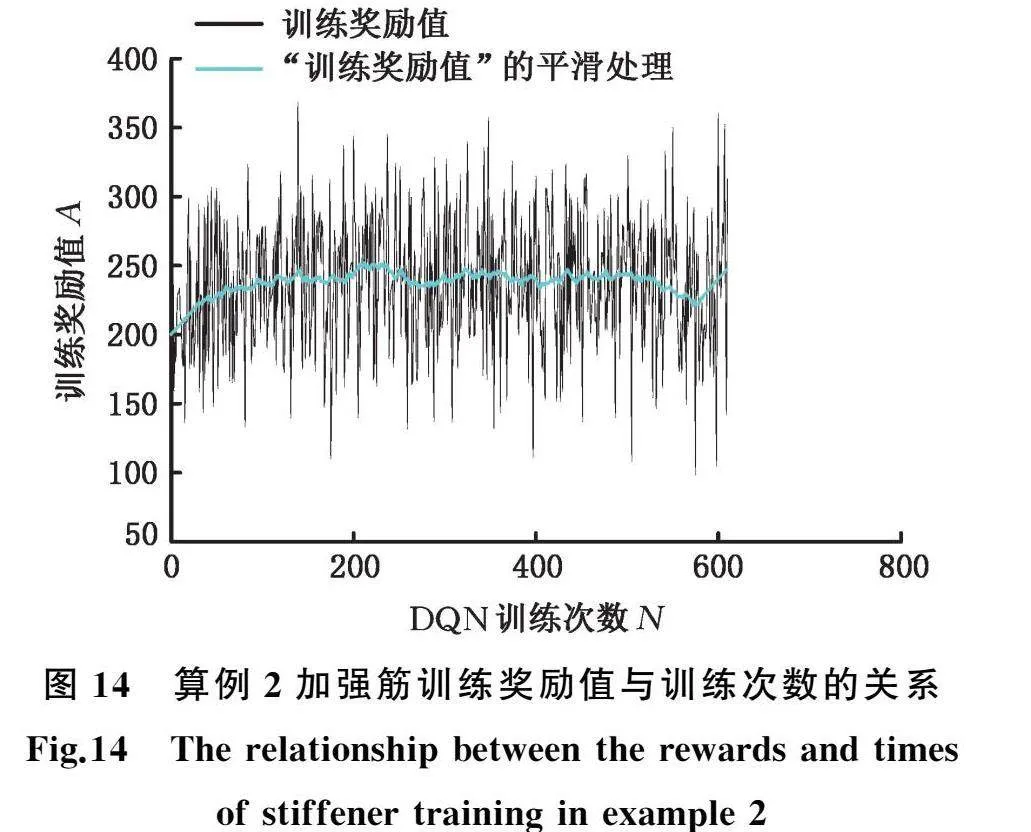
在本算例中，设置加强筋生长“种子”数量为3，分别位于方板约束边的顶点A、D与受力点P，如图13所示。加强筋训练奖励值与训练次数之间的关系如图14所示。由图14可知，训练奖励值具有上升并波动收敛的趋势，这说明随着训练次数的增加，加强筋愈发朝着能够减小更多应变能的方向生长，证明了所提出的基于多智能体深度Q网络交互的板壳加强筋生长式设计的有效性。

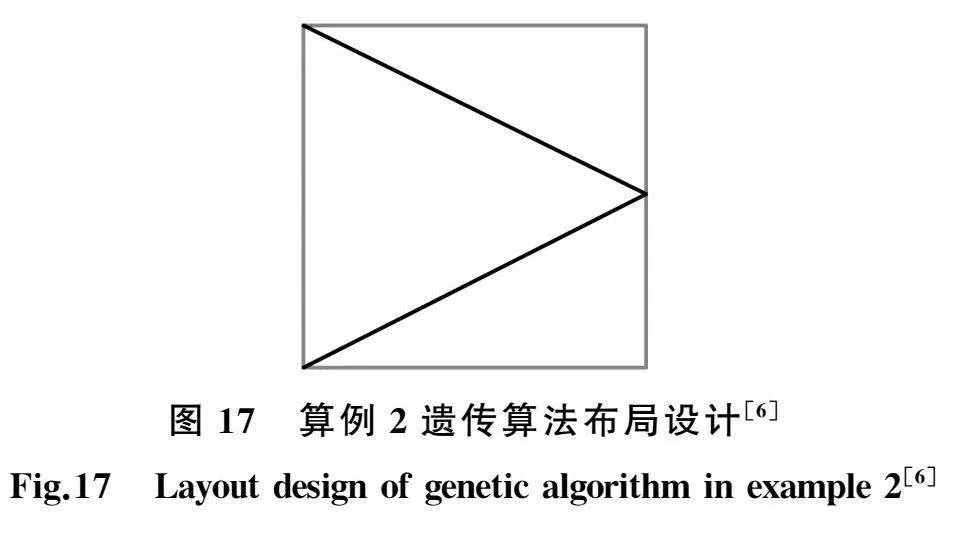
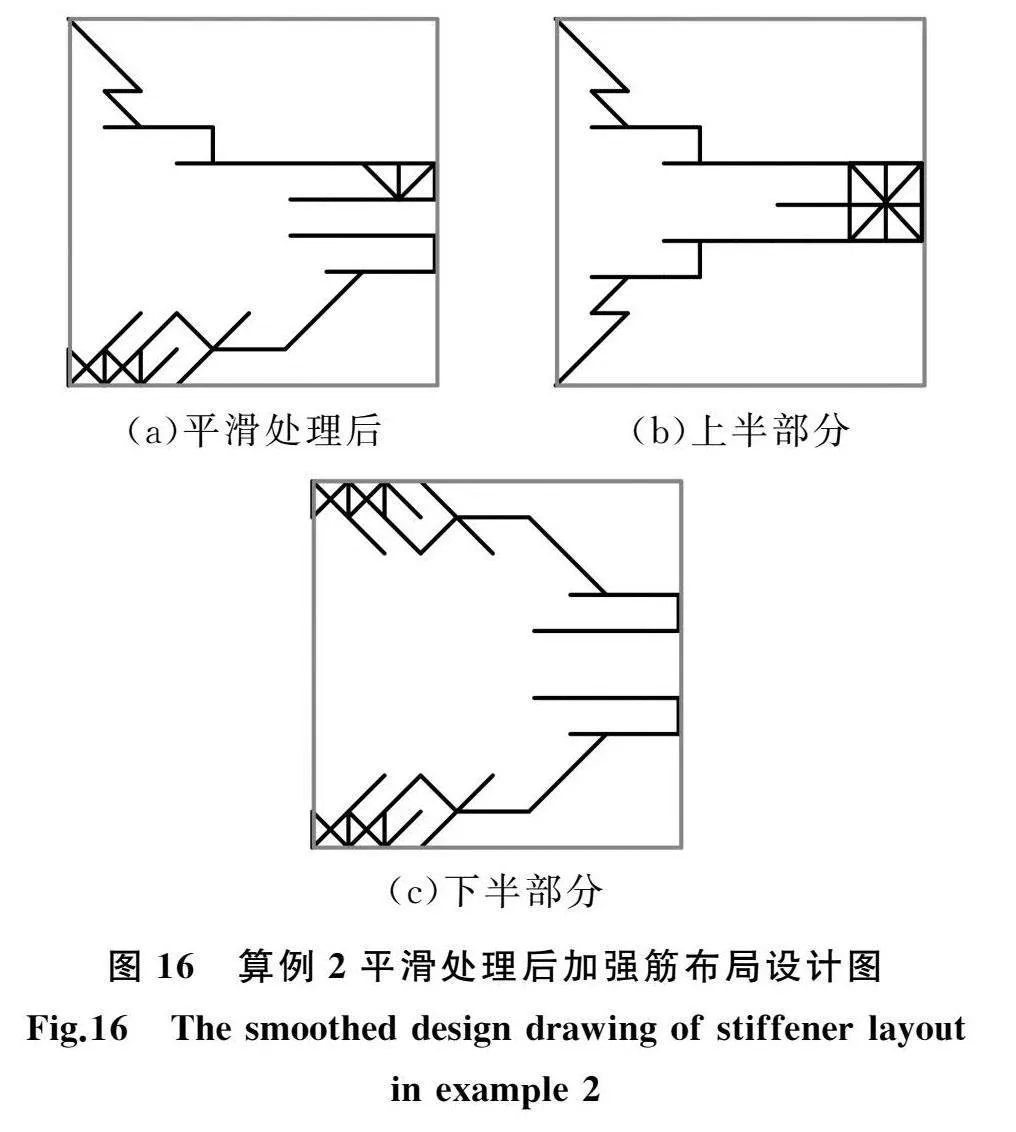
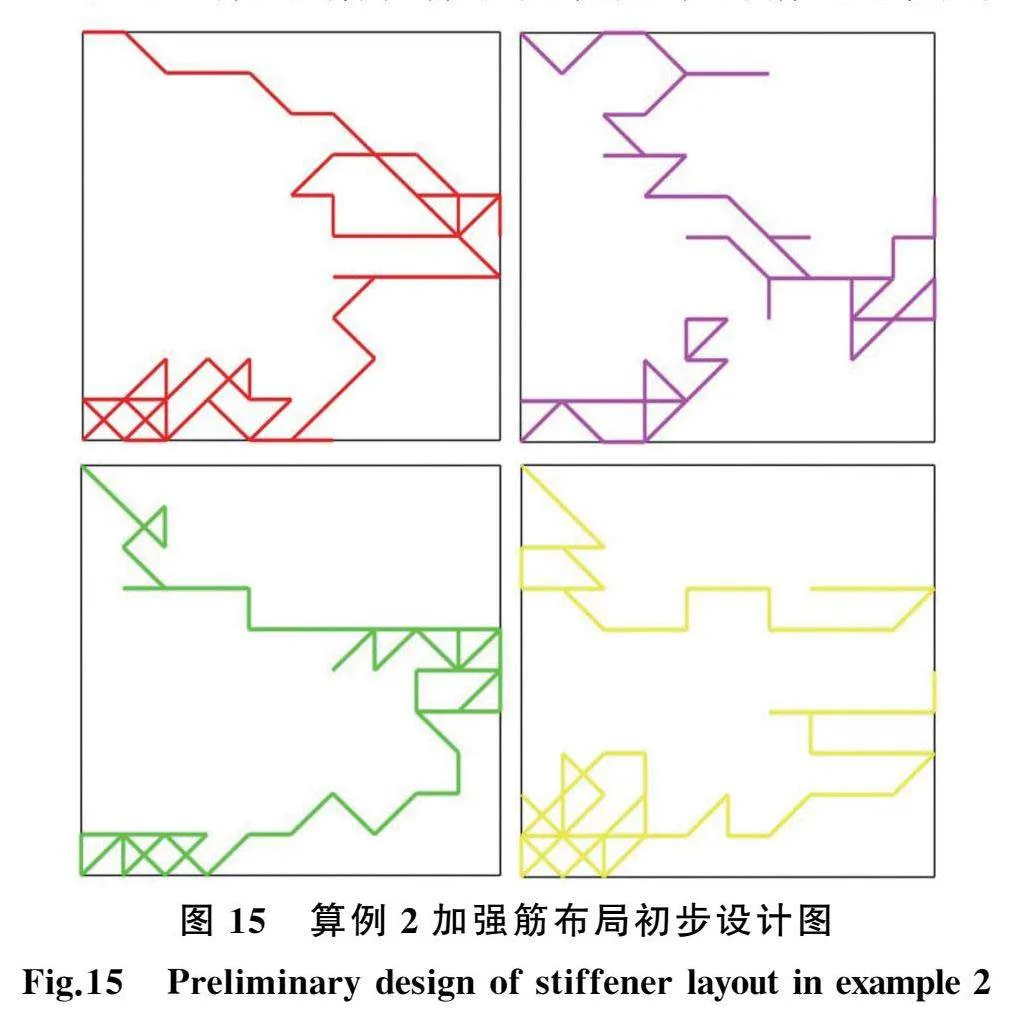
根据智能体训练情况，得到加强筋生长式布局的初步设计结果，如图15所示。对图15所示的四张加强筋生长式布局的初步设计结果进行叠加，取加强筋重叠部分，去除单独的加强筋，得到平滑处理后的加强筋布局设计图（图16）。根据本工况中方形薄板所承受的载荷、约束以及结构的对称性，显然其加强筋应当为对称式分布。因此，分别对图16a的上半部分与下半部分进行对称处理，最终得到加强筋生长式设计图（图16b、图16c）。从最终设计结果可以看出，本文方法得到的结果（图16b、图16c）与遗传算法［6］得到的设计布局（图17）整体上一致，加强筋分布清晰合理，说明本文方法能够有效地解决加强筋分布设计问题。以应变能数值表征刚度，图16b的加强筋三维设计图见图18a，经仿真计算得出结论如下：加强筋材料体积增加量为7.22%，应变能减小26.57%。图16c的加强筋三维设计图见图18b，经仿真计算得出结论如下：加强筋材料体积增加量为8.99%，应变能减小19.57%。比较后可知，图18a所示的加强筋在体积变化更小的情况下具有更大的应变能减小量，故性能更优。

5 结论

（1）本文运用马尔可夫决策过程对板壳加强筋生长过程进行建模，通过多智能体深度Q网络与加强筋生长环境的交互，实现了板壳加强筋的生长式设计。

（2）通过引入多智能体、共享状态奖励并记忆特定动作，降低了学习复杂度，最终实现奖励值的波动收敛，达成板壳加强筋生长式设计策略。

（3）通过经典算例验证了本文基于多智能体深度Q网络交互的板壳加强筋生长式设计的有效性，最终得到了清晰合理的加强筋设计布局。

本文论述的基于多智能体深度Q网络交互的板壳加强筋生长式设计方法的实现过程印证了该方法在理论上对不同的板壳及受载工况均具有普适性。然而，由于该方法的研究仍然处于初步阶段，故优先且着重考虑采用共识性算例来验证其可行性与正确性，以期为后续进一步研究提供有效性支撑。后续将引入更为复杂的工况，以研究相关设计变量对优化结果的影响。

参考文献：

［1］ MA Xiangtao， WANG Fayao， AAGE N， et al. Generative Design of Stiffened Plates Based on Homogenization Method［J］. Structural and Multidisciplinary Optimization， 2021， 64（6）：3951-3969.

［2］ WANG Bo， TIAN Kuo， HAO Peng， et al. Hybrid Analysis and Optimization of Hierarchical Stiffened Plates Based on Asymptotic Homogenization Method［J］. Composite Structures， 2015， 132：136-147.

［3］ BENDS E M P， SIGMUND O. Material Interpolation Schemes in Topology Optimization［J］. Archive of Applied Mechanics， 1999， 69（9）：635-654.

［4］ LI Pengfei， WU Yi， YVONNET J. A SIMP-phase Field Topology Optimization Framework to Maximize Quasi-brittle Fracture Resistance of 2D and 3D Composites［J］. Theoretical and Applied Fracture Mechanics， 2021， 114：102919.

［5］ LI Baotong， LIU Honglei， YANG Zihui， et al. Stiffness Design of Plate/Shell Structures by Evolutionary Topology Optimization［J］. Thin-Walled Structures， 2019， 141：232-250.

［6］ FATEMI J， TROMPETTE P. Optimal Design of Stiffened Plate Structures［C］∥43rd AIAA/ASME/ASCE/AHS/ASC Structures， Structural Dynamics， and Materials Conference. Reston， 2002：1672.

［7］ MULANI S B， SLEMP W C H， KAPANIA R K. EBF3PanelOpt：an Optimization Framework for Curvilinear Blade-stiffened Panels［J］. Thin-Walled Structures， 2013， 63：13-26.

［8］ 张卫红， 章胜冬， 高彤. 薄壁结构的加筋布局优化设计［J］. 航空学报， 2009， 30（11）：2126-2131.

ZHANG Weihong， ZHANG Shengdong， GAO Tong. Stiffener Layout Optimization of Thin Walled Structures［J］. Acta Aeronautica et Astronautica Sinica， 2009， 30（11）：2126-2131.

［9］ ZHANG Weisheng， YUAN Jie， ZHANG Jian， et al. A New Topology Optimization Approach Based on Moving Morphable Components（MMC） and the Ersatz Material Model［J］. Structural and Multidisciplinary Optimization， 2016， 53（6）：1243-1260.

［10］ 崔荣华， 崔天晨， 孙直， 等. 基于水平集法的薄板加强筋分布优化理论研究［J］. 固体力学学报， 2018， 39（6）：587-593.

CUI Ronghua， CUI Tianchen， SUN Zhi， et al. Topology Optimization for Stiffener Layout of Thin Plate Structures Based on Level Set Method［J］. Chinese Journal of Solid Mechanics， 2018， 39（6）：587-593.

［11］ DING Xiaohong， YAMAZAKI K. Adaptive Growth Technique of Stiffener Layout Pattern for Plate and Shell Structures to Achieve Minimum Compliance［J］. Engineering Optimization， 2005， 37（3）：259-276.

［12］ LI Yongxin， XUE Kai. Mechanics in Leaf Venation Morphogenesis and Their Biomimetic Inspiration to Construct a 2-dimensional Reinforcement Layout Model［J］. Journal of Biomimetics， Biomaterials and Tissue Engineering， 2011， 10：81-93.

［13］ 薛开， 李永欣. 板壳结构加筋布局的仿生脉序生长算法［J］. 哈尔滨工程大学学报， 2011， 32（9）：1262-1266.

XUE Kai， LI Yongxin. A Bionic Venation Growth Algorithm for a Stiffener Layout in Plate/Shell Structure［J］. Journal of Harbin Engineering University， 2011， 32（9）：1262-1266.

［14］ SHEN Lei， DING Xiaohong， HU Tiannan， et al. Simultaneous Optimization of Stiffener Layout of 3D Box Structure Together with Attached Tuned Mass Dampers under Harmonic Excitations［J］. Structural and Multidisciplinary Optimization， 2021， 64（2）：721-737.

［15］ 张坤鹏， 郝鹏， 段于辉， 等. 基于深度学习的多级曲线加筋壁板布局优化设计［J］. 中国舰船研究， 2021， 16（4）：86-95.

ZHANG Kunpeng， HAO Peng， DUAN Yuhui， et al. Layout Optimization Design of Hierarchical Curvilinearly Stiffened Panels Based on Deep Learning［J］. Chinese Journal of Ship Research， 2021， 16（4）：86-95.

［16］ 董伟， 李扬， 辛克浩， 等. 基于拓扑优化的点阵-加筋板式结构设计方法［J］. 西北工业大学学报， 2021， 39（6）：1233-1239.

DONG Wei， LI Yang， XIN Kehao， et al. A Method of Designing Plate Structure Consisting of Lattices and Stiffeners Based on Topology Optimization［J］. Journal of Northwestern Polytechnical University， 2021， 39（6）：1233-1239.

［17］ SINGH K， KAPANIA R K. Accelerated Optimization of Curvilinearly Stiffened Panels Using Deep Learning［J］. Thin-Walled Structures， 2021， 161：107418.

［18］ LIU Dachuan， HAO Peng， XU Tengfei， et al. Intelligent Optimization of Stiffener Unit Cell via Variational Autoencoder-based Feature Extraction［J］. Structural and Multidisciplinary Optimization， 2022， 66（1）：8.

［19］ 丁晓红， 李国杰， 蔡戈坚， 等. 薄板结构的加强筋自适应成长设计法［J］. 中国机械工程， 2005， 16（12）：1057-1060.

DING Xiaohong， LI Guojie， CAI Gejian， et al. Adaptive Growth Method of Rib Distribution for Thin Plate Structure［J］. China Mechanical Engineering， 2005， 16（12）：1057-1060.

［20］ GUO Xu， ZHANG Weisheng， ZHONG Wenliang. Topology Optimization Based on Moving Deformable Components：a New Computational Framework［EB/OL］. 2014：arXiv：1404.4820. http：∥arxiv.org/abs/1404.4820.

（编辑 陈 勇）