高速列车车轮两阶段退化建模及可靠性分析

摘要：针对高速列车车轮在退化过程中呈现两阶段特征的问题，提出一种基于两阶段非线性Wiener过程的高速列车车轮退化建模及可靠性分析方法。采用CUSUM（CUmulative SUM）算法实现车轮退化过程变点判别，在此基础上，利用马尔可夫链蒙特卡罗方法估计模型未知参数。针对车轮两阶段退化过程较为复杂、可靠度解析形式难以求解的问题，通过蒙特卡罗模拟方法求解得到车轮可靠度函数曲线和可靠寿命。最后以某机车同转向架车轮单个镟修周期内的实测数据为例，验证了模型的有效性。结果表明：受运营环境影响，同转向架不同侧车轮退化过程出现变点的位置不同；相较于未考虑阶段性特征的退化模型，所提模型可靠性评估结果更符合现场实际；通过不断获取车轮退化数据，可采用所提模型计算并更新车轮可靠寿命值，为车轮镟修周期的进一步优化提供了理论指导。

关键词：高速列车车轮；两阶段Wiener过程；可靠度；退化建模；蒙特卡罗模拟

中图分类号：U268.3

DOI：10.3969/j.issn.1004132X.2024.08.007

开放科学（资源服务）标识码（OSID）：

Modeling and Reliability Analysis of Wheel Two-stage Degradation of

High-speed Trains

QI Jinping1，2，3 LIU Xiaoyu1 FENG Hong1 LI Hongwei1 YAN Daqiang4

1.Mechatronics Tamp;R Institute，Lanzhou Jiaotong University，Lanzhou，730070

2.Gansu Provincial Engineering Technology Center for Informatization of Logistics amp; Transport

Equipment，Lanzhou，730070

3.Gansu Provincial Industry Technology Center of Logistics amp; Transport Equipment，Lanzhou，730070

4.Locomotive Department，China Railway Lanzhou Group Co.，Ltd.，Lanzhou，730070

Abstract： Aiming at the problems that high-speed train wheels showed phased characteristics in the degradation processes， a modeling and reliability analysis method of high-speed train wheel degradation was proposed based on two-stage Wiener process. On the basis of the Markov chain Monte-Carlo（MCMC） method to estimate the unknown parameters of the model， the reliability function curve and reliability life of the wheel were obtained by Monte-Carlo simulation method for the problems that the two-stage degradation processes of the wheel were complex and the reliability analysis form was difficult to solve. Finally， the effectiveness of the model was verified by taking the measured data of a locomotive and bogie wheel in a single repair cycle as an example. The results show that due to the operating environment， the change point position of the wheel degradation processes on different sides of the bogie is different. Compared with the reliability evaluation results of the degradation model without considering the phased characteristics， the proposed model is more in line with the actual field situation. According to the reliable life prediction results， affected by the operating environment， the wheel degradation processes on different sides of the bogie has different changing point positions. By continuously obtaining the wheel degradation data， the reliable life value of the wheels may be calculated and updated by using the model proposed herein， which provides theoretical guidance for the further optimization of the wheel repair cycle.

Key words： high-speed train wheel; two-stage Wiener process; reliability; degenerate modeling; Monte-Carlo simluation

0 引言

高速列车运行时，由于轮对的特殊结构，两个不同直径车轮的轮缘同钢轨接触并产生磨损，当一侧轮缘厚度磨耗超限时，会影响列车的正常运行，严重时甚至会造成脱轨，因此，分析车轮的退化规律对保证高速列车运营安全具有重要意义。

当前对高速列车车轮可靠性分析的研究主要分为基于动力学仿真模型以及基于性能退化模型两种。JENDEL［1］提出了基于Archard的车轮磨耗预测模型，以此预测了瑞典首都铁路网的磨耗。杨斌等［2］利用Tγ/A磨损率函数对车轮踏面的磨耗进行仿真分析，结果表明外轨处车轮磨耗比内轨车轮更严重，同时该模型的仿真结果比Archard模型具有更高的精度。黎嘉欣等［3］利用实测的车轮磨耗数据对Tγ/A磨损率函数进行修正，并对磨耗预测模型进行验证。TAO等［4］认为钢轨弹性会对车轮磨耗仿真结果存在一定影响。王璞等［5］通过多工况仿真并引入权重因子来模拟实际复杂运行线路条件，建立了重载货车车轮磨耗发展的数值预测模型。然而由于高速列车在实际运营、线路环境等方面的不确定性以及车轮失效形式的多样性，使得动力学仿真模型难以精确评估车轮可靠性。

当前基于性能退化的高速列车车轮可靠性分析的研究报道较少。张义民等［6］基于非平稳Gamma过程建立了车轮轮缘退化模型，预测了0.95可靠度条件下车轮的可靠寿命。SHI等［7］建立了一种基于非线性Wiener过程的车轮踏面退化模型，基于车轮实时监测数据实现了模型参数的在线更新和车轮剩余使用寿命的实时预测。LI等［8］提出了一种考虑测量误差的车轮寿命预测模型，在考虑测量误差的基础上将在线数据与先验信息相结合，提高了寿命预测精度。吕昊等［9］基于Copula函数建立了车轮退化相关模型，分析了车轮踏面滚动圆直径与轮缘厚度间的相关关系，并对车轮的可靠寿命进行了预测。DAI等［10］提出了一种基于条件二元Gamma过程的车轮轮缘退化模型，研究了车轮轮缘的失效规律，评估了不同车厢车轮在不同阶段的可靠性水平。上述研究从多个角度建立了高速列车车轮性能退化模型，评估了车轮可靠性，但由于疲劳裂纹扩展等失效机理，通常车轮在退化过程中会存在阶段性特征，即退化过程中存在变点，变点前后退化速率存在一定差异［11］，故有必要考虑车轮在退化过程中呈现的阶段性特征。

针对上述问题，本文以高速列车同转向架车轮为研究对象，采用两阶段非线性Wiener过程建立高速列车车轮两阶段退化模型，利用CUSUM算法得到同转向架不同车轮的变点位置，通过蒙特卡罗（Monte Carlo）模拟求解得到车轮可靠度曲线及可靠寿命，为现场车轮镟修周期的优化提供理论指导。

1 车轮退化规律分析

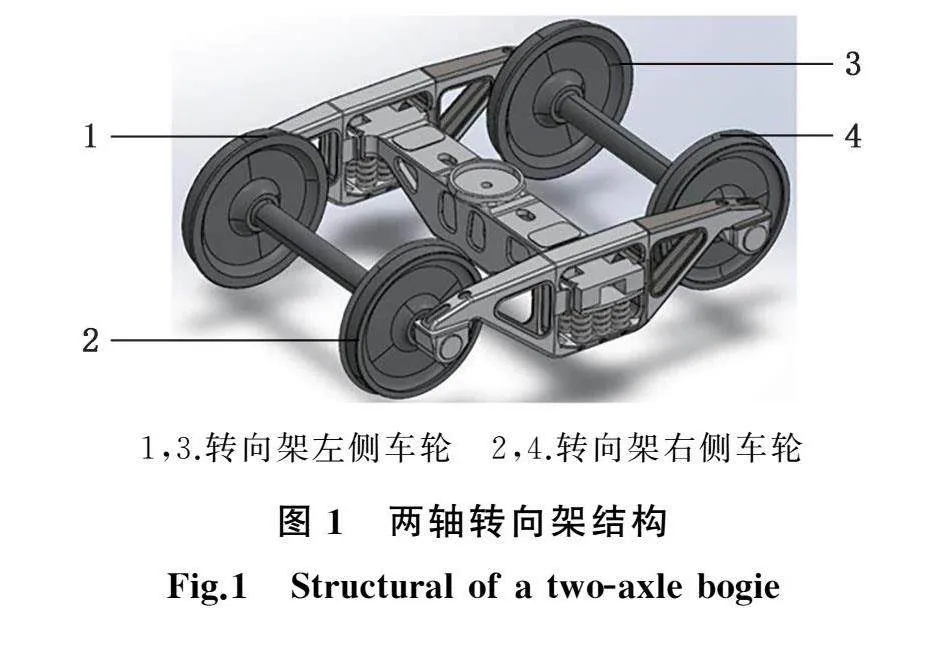
车轮是高速列车转向架的关键部件，它通过过盈配合与车轴组合在一起，两轴转向架结构如图1所示。轮缘作为车轮的重要组成部分，对维持高速列车运行的稳定性具有重要作用。在高速列车运行过程中，当车辆经过曲线路段时会造成轮缘厚度磨损，随着轮缘厚度磨损的增加，会加大车轮与钢轨间的导向间隙，进而加剧列车在运行时的横向移动，对列车的运行安全性造成一定影响［12］，同时车轮表面硬度逐渐降低，当表面硬度降至一定限度时，车轮磨耗速率进一步加快。在实际情况中，由于车轮在制造、检修、运营环境等方面存在一定差异，导致不同车轮间退化速率存在一定差异［13］。

2 车轮两阶段退化建模

假设对某高速列车N个车轮进行M次尺寸检测，令xij为第j次检测时第i个车轮的尺寸退化量，i=1，2，…，N，j=1，2，…，M，则车轮尺寸退化量检测值矩阵可以表示为

Xij=x11x12…x1Mx21x22…x2MxN1xN2…xNM

对于车轮退化过程中呈现的两阶段特征，为不失一般性，基于非线性Wiener过程建立以下退化模型：

Xi（t）=［μi1Λi1（t）+σi1B（Λi1（t））］I（0，τi］（t）+

［Xi（τi）+μi2Λi2（t－τi）+

σi2B（Λi2（t－τi））］I（τi，∞）（t）（1）

Λi1（t）=tγi1" Λi2（t-τi）=（t-τi）γi2

式中，t为列车运行里程，μi1、μi2分别为车轮i在第一和第二阶段的漂移系数；σi1、σi2分别为车轮i在第一和第二阶段的扩散系数；τi为车轮i的变点，即当列车运行至τi时，车轮i的退化过程由第一阶段进入第二阶段；Xi（τi）为车轮i在列车运行至τi时的退化量，即第二阶段的退化初值；B（·）为标准布朗运动；Λi1（t）、Λi2（t-τi）为时间尺度变换函数，分别为车轮i退化过程在各阶段的非线性特征；γi1、γi2为退化时间的指数；I（0，τi］（t）、I（τi，∞）（t）为示性函数。

综上可得

μi=μi1I（0，τi］（tj）+μi2I（τi，∞）（tj）

σi=σi1I（0，τi］（tj）+σi2I（τi，∞）（tj）

ΔΛi（tj）=ΔΛi1（tj）I（0，τi］（tj）+ΔΛi2（tj）I（τi，∞）（tj）（2）

令ΔXij=Xi（tj）-Xi（tj-1）表示车轮i在里程段［tj-1，tj］上的退化增量，由Wiener过程性质可知，退化增量ΔXij在变点τi前后分别服从不同参数的正态分布：

ΔXij～N（μi·ΔΛi（tj），σ2i·ΔΛi（tj））（3）

其累积分布函数和概率密度函数分别为

Fi（ΔXij）=Φ（ΔXij－μi·ΔΛi（tj）σ2i·ΔΛi（tj））（4）

fi（ΔXij）=12πσ2i·ΔΛi（tj）·

exp（ΔXij－μi·ΔΛi（tj））22σ2i·ΔΛi（tj）（5）

式中，Φ（·）为标准正态分布的累计分布函数。

3 车轮退化过程变点判别与参数估计

3.1 基于CUSUM算法的变点判别

由Wiener过程定义可知，X（t）期望的变化会导致漂移系数μ发生变化，进而反映设备的退化速率。因此，可以采用CUSUM算法识别退化数据中期望发生改变的点，进而判别出车轮退化过程中的分段点。CUSUM算法计算每个数据值与目标值之间偏差的累积和，通过累加“小偏差”达到放大的效果，即使退化数据均值发生微小变化也会导致累积偏差值的增加或降低，从而对退化过程中的分段点进行识别［14］。步骤如下：

（1）计算某车轮退化数据的期望：

x-=1M∑Mj=1xj（6）

式中，xj为第j次尺寸检测时车轮退化量，j=1，2，…，M。

（2）令S0=0，S1=S0+（x1-x-），S2=S1+（x2-x-），…，Sj=Sj-1+（xj-x-），由此可以求得累积和S1，S2，…，SM。

（3）根据S1到SM的单调性变化情况判断变点位置，单调性发生变化的点即该车轮退化过程的变点。

3.2 基于MCMC方法的参数估计

根据3.1节求得变点τi，可将车轮i的退化数据分为2段，根据Wiener过程性质建立各段退化数据对应的似然函数。对于（t1，t2，…，tτi）里程上的退化数据，结合式（5）可得似然函数：

L1=∏Ni=1∏τij=1fi（ΔXij）=

∏Ni=1∏τij=1（12πσ2iΔΛi（tj）exp（ΔXij－μiΔΛi（tj））22σ2iΔΛi（tj））（7）

相应的对数似然函数为

ln L1=∑Ni=1∑τij=1ln（fi（ΔXij））=

∑Ni=1∑τij=1ln（12πσ2iΔΛi（tj）

exp（ΔXij－μiΔΛi（tj））22σ2iΔΛi（tj））（8）

类似地，（tτi+1，tτi+2，…，tM）里程上退化数据的对数似然函数为

ln L2=∑Ni=1∑Mj=τi+1ln（fi（ΔXij））=

∑Ni=1∑Mj=τi+1ln（12πσ2iΔΛi（tj）

exp（ΔXij－μiΔΛi（tj））22σ2iΔΛi（tj））（9）

由式（8）、式（9）可得，在里程（t1，t2，…，tM）上的对数似然函数为

ln Lt=ln L1+ln L2（10）

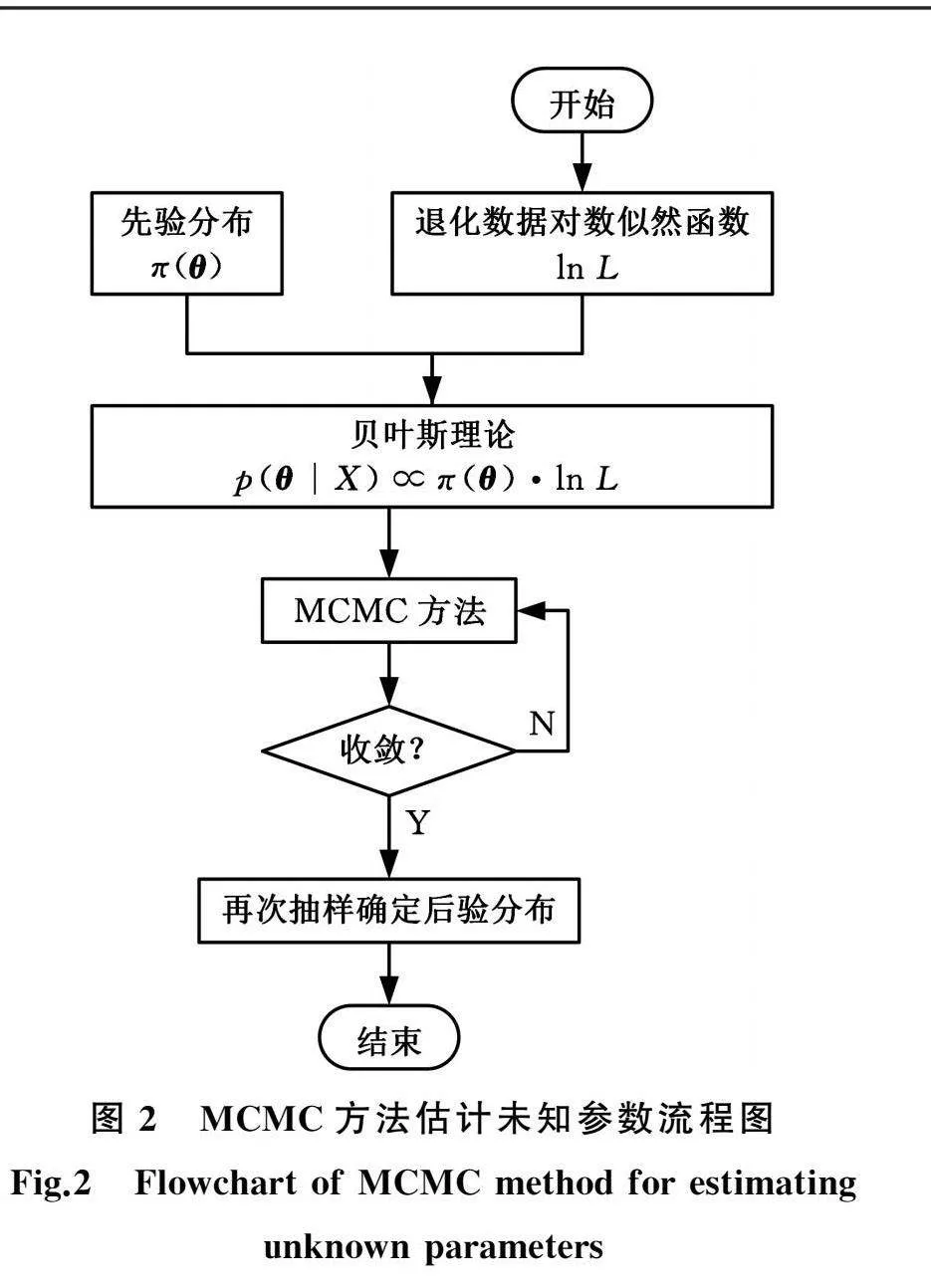
考虑到式（10）中未知参数较多，采用马尔可夫链蒙特卡罗（Markov chain Monte Carlo ，MCMC）方法求解未知参数，其思想是建立马尔可夫链，对未知变量进行模拟，当马尔可夫链达到稳态时即得到所求参数［15-16］。根据贝叶斯定理，可得未知参数的联合后验分布：

p（θ|X）∝π（θ）·ln Lt（11）

θ=（μi1，μi2，σi1，σi2，γi1，γi2）

根据经验给定未知参数的联合先验分布π（θ），流程如图2所示。

4 车轮可靠性评估

由于高速列车车轮两阶段退化过程较为复杂，难以求得可靠度的解析形式，故提出一种基于蒙特卡罗模拟的车轮可靠度计算方法［17-18］。其基本原理是应用随机抽样技术得到符合待求解分布的样本，通过对样本值的观察与统计，实现对未知分布的分析。

根据求得的变点及模型未知参数估计结果，仿真得到样本容量为Q的车轮仿真退化数据，统计各样本失效里程Tw，其中w=1，2，…，Q；统计里程为t时未失效车轮的样本个数Qw，即满足Twgt;t的样本个数，则里程为t时车轮可靠度R（t）=Qw/Q。仿真步骤如下：

（1）设定仿真时长和步长等参数，为确保样本车轮在仿真期间内发生失效，仿真时长应尽量长一些。设仿真步长为Δt，仿真时刻数为L，则仿真时长为LΔt。

（2）根据式（4）生成仿真时间段［（s-1）Δt，sΔt］内的退化增量ΔX（sΔt），其中s=1，2，…，L。

（3）重复步骤（2），得到仿真时长内退化增量：［ΔX（Δt）ΔX（2Δt）…ΔX（LΔt）］。

（4）对退化增量求和，得到仿真样本在各仿真时刻退化量：［X（Δt）X（2Δt）…X（LΔt）］。

（5）重复步骤（2）～（4）即可得到样本容量为Q的仿真退化数据。

5 实例分析

为验证模型的有效性，选取某机车同一转向架4个车轮在同一镟修周期内前25万km轮缘厚度实测退化数据进行实例分析，以轮缘厚度段修标准3 mm为失效阈值，退化趋势如图3所示。

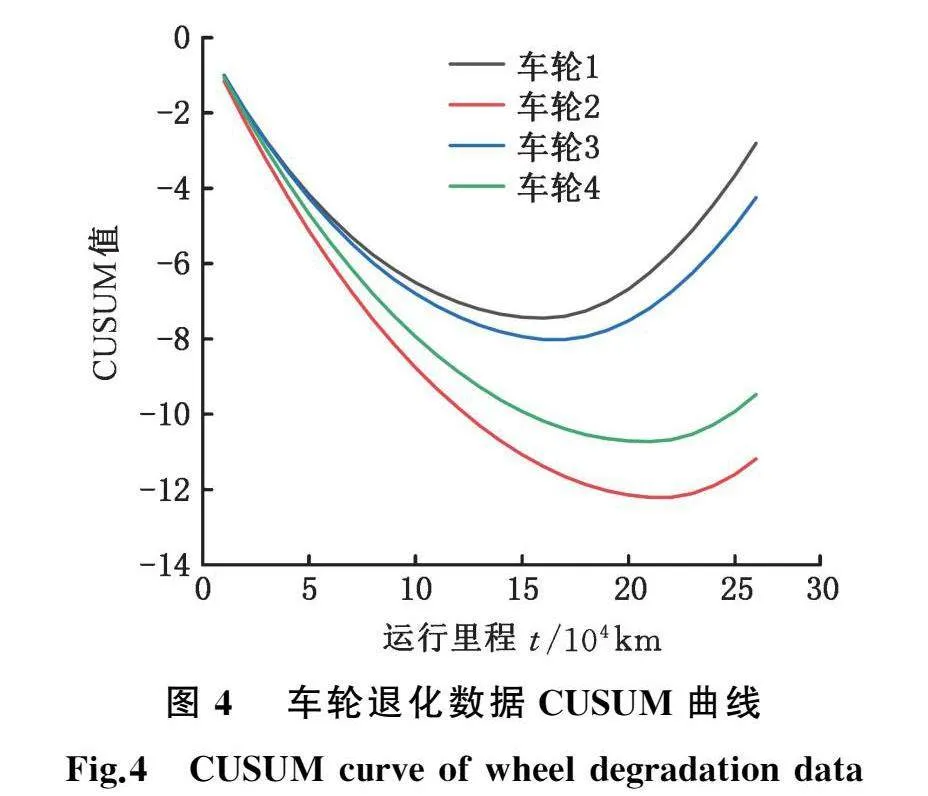
根据3.1节CUSUM方法判别车轮退化过程变点，结果如图4所示。由图4可知，车轮退化过程可以分为两个阶段：在第一阶段，车轮退化数据与对应样本期望偏差的累积和不断减小，车轮退化速率较慢；在第二阶段，车轮退化数据与对应样本均值偏差的累积和不断增大，退化速率变快。同时，车轮1、3退化过程中出现变点里程在16万km处，车轮2、4出现变点里程在21万km处，这是由于在同一转向架中，车轮1、3位于左侧，车轮2、4位于右侧，受列车运营线路条件、环境等因素影响，导致同转向架不同侧车轮出现变点的位置会有一定差异。可见该列车运行线路左侧曲线段较多，导致转向架左侧车轮磨耗现象相较于右侧更为严重［19］，出现变点位置更早。

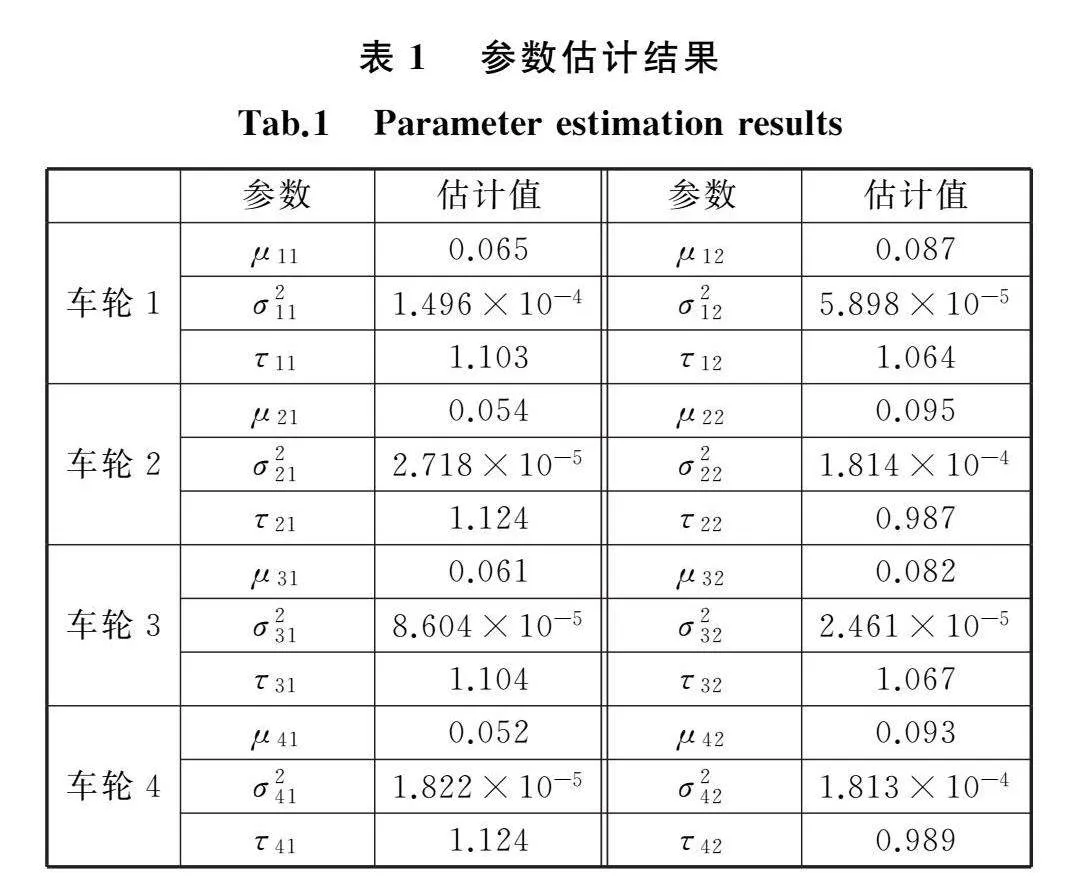
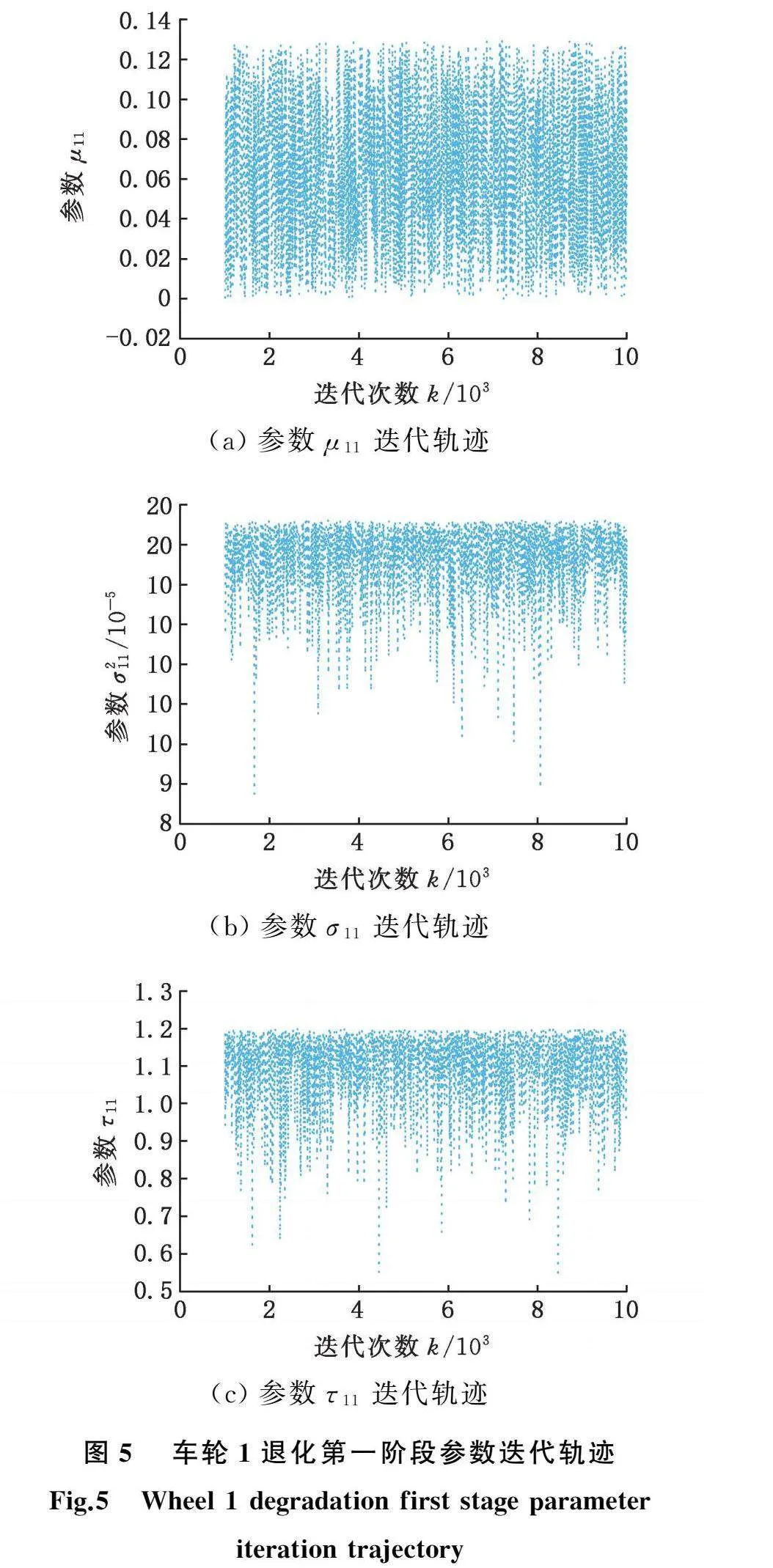
根据所求变点及3.2节所述MCMC方法对4个样本车轮分别进行参数估计，利用OpenBugs软件进行10 000次Gibbs抽样，取第1001～10 000次迭代数据用于参数估计，参数估计结果见表1。以车轮1第一阶段为例绘制参数迭代轨迹，如图5所示。

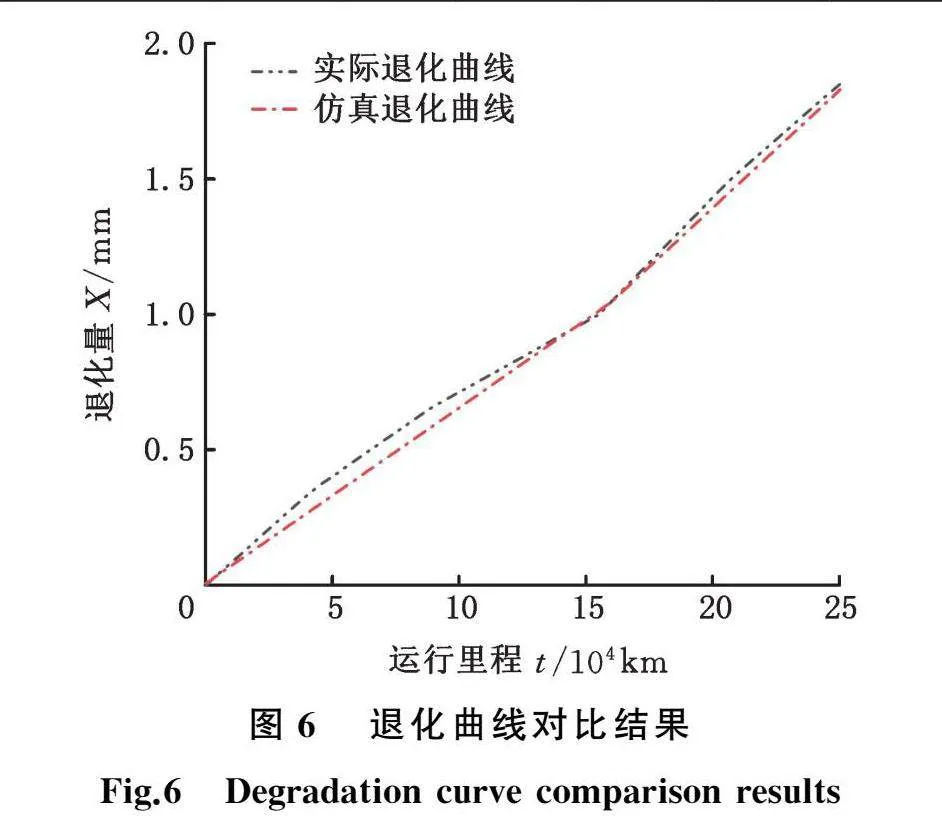
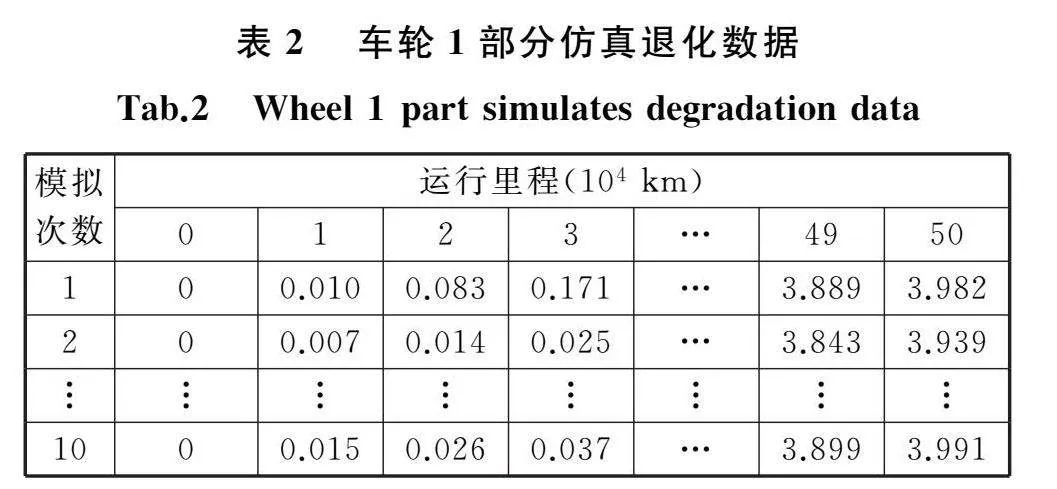
由表1可知，各车轮在不同阶段退化模型参数均有较大差异，说明在不同阶段各车轮退化速率均发生了变化。根据表1中参数估计结果，设定仿真步长Δt=0.1，仿真次数N=104，分别生成车轮1～车轮4退化仿真数据，车轮1部分退化模拟数据见表2。为验证模型拟合效果，以车轮1为例给出模拟数据退化曲线与实测数据退化曲线的对比结果，如图6所示，可以看出所提模型的退化曲线能有效地描述车轮的退化规律。

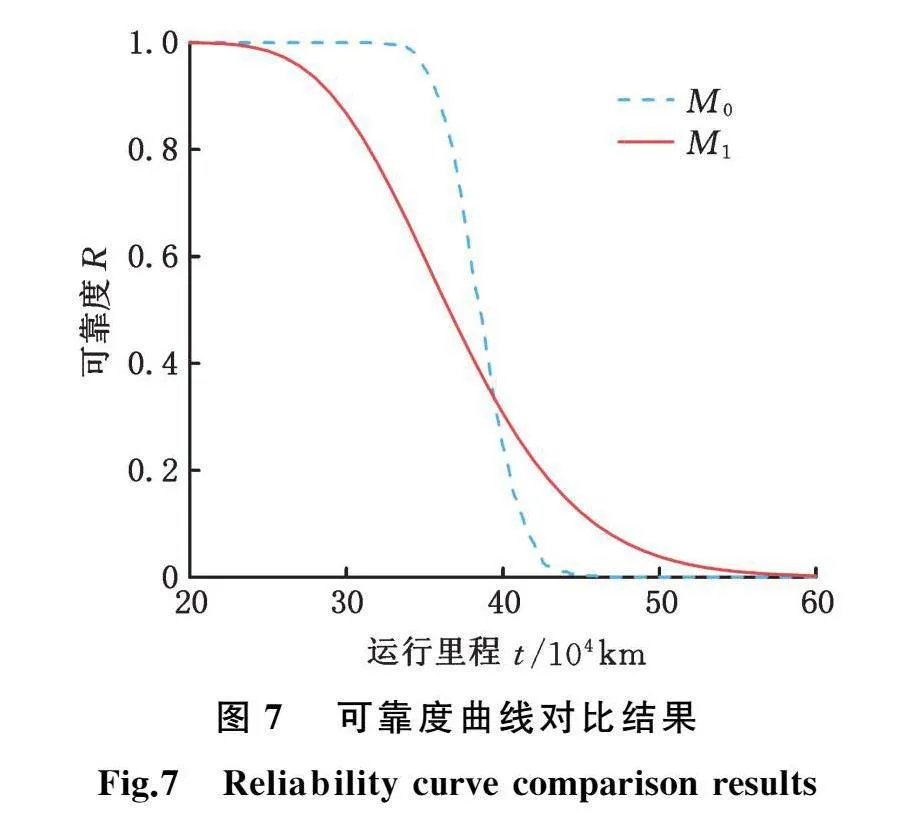
进一步，令本文模型为M0，不考虑阶段性的Wiener过程退化模型为M1［20］，以车轮1为例对比两种模型的可靠度评估结果，结果如图7所示。

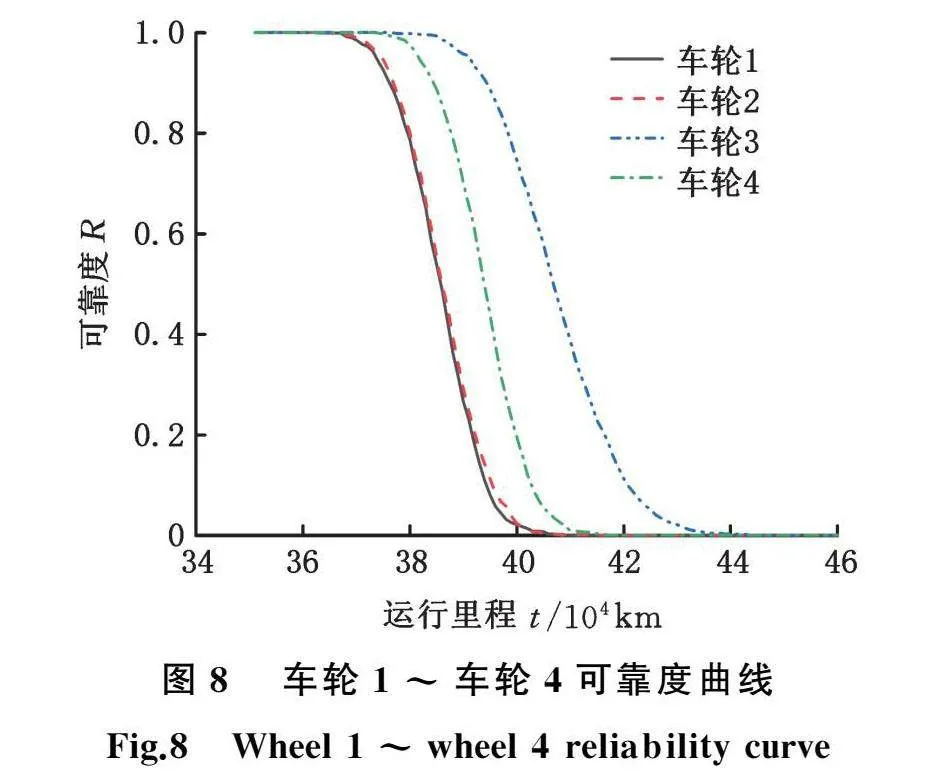
同时，基于模型M0对车轮1～车轮4分别进行可靠性评估，结果如图8所示。

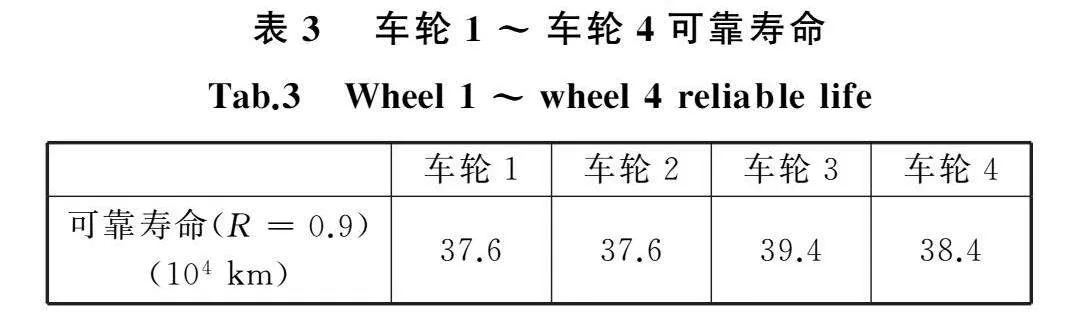
由图7可知，相较于模型未考虑阶段性的退化模型M1，本文模型M0可靠性评估结果在后期更加保守，为保证列车运行安全，选用模型M0进行可靠性评估效果更好。为进一步指导现场，分别计算各车轮可靠寿命，结果见表3。根据表3数据，建议列车在镟修后运行37.5万km时检查车轮退化情况，并制定相应检修策略。

6 结论

（1）由于列车运营环境左侧曲线段较多，同转向架不同侧车轮出现变点位置不同，左侧车轮退化过程中出现变点位置约比右侧车轮早5万km，故在制定检修策略时应考虑线路环境等因素对车轮磨耗的影响。

（2）相较于未考虑阶段性的退化模型，本文模型在可靠性评估后期结果较为保守，更加贴合工程实际。

（3）根据各车轮可靠寿命计算结果，建议列车在前次镟修后运行37.5万km时检查各车轮退化情况，同时，随着退化数据的不断积累，通过本文模型计算更新后续车轮可靠寿命值，从而进一步指导车轮后续镟修周期的确定。

参考文献：

［1］ JENDEL T. Prediction of Wheel Profile Wear—Comparisons with Field Measurements［J］. Wear， 2002， 253（1/2）：89-99.

［2］ 杨斌， 郭立昌， 郭俊， 等. 基于Tγ/A-磨损率模型的车轮磨耗仿真分析［J］. 机械工程学报， 2017， 53（22）：101-108.

YANG Bin， GUO Lichang， GUO Jun， et al. Simulation Analysis of Wheel Wear Based on the Model of Tγ/A-wear Rate［J］. Journal of Mechanical Engineering， 2017， 53（22）：101-108.

［3］ 黎嘉欣， 陶功权， 刘希政， 等. 基于两种轨道线路建模方法的地铁车轮磨耗预测对比分析［J］. 工程力学， 2022， 39（6）：226-235.

LI Jiaxin， TAO Gongquan， LIU Xizheng， et al. Comparative Analysis of Metro Wheel Wear Prediction Based on Two Track Modeling Methods［J］. Engineering Mechanics， 2022， 39（6）：226-235.

［4］ TAO Gongquan， REN Dexiang， WANG Linfeng， et al. Online Prediction Model for Wheel Wear Considering Track Flexibility［J］. Multibody System Dynamics， 2018， 44（3）：313-334.

［5］ 王璞， 王树国. 复杂运营条件下重载货车车轮磨耗发展的数值预测［J］. 同济大学学报（自然科学版）， 2019， 47（1）：71-78.

WANG Pu， WANG Shuguo. Numerical Prediction of Wheel Wear Development of Heavy-haul Freight Car under Complex Operation Conditions［J］. Journal of Tongji University （Natural Science）， 2019， 47（1）：71-78.

［6］ 张义民， 林禄样， 吕昊. 基于Gamma过程的机车车轮镟修里程预测方法［J］. 东北大学学报（自然科学版）， 2018， 39（4）：522-526.

ZHANG Yimin， LIN Luyang， LYU Hao. Prediction Method of Locomotive Wheel Degradation Based on Gamma Process［J］. Journal of Northeastern University （Natural Science）， 2018， 39（4）：522-526.

［7］ SHI Hongmei， YANG Jinsong， SI Jin. Centralized Maintenance Time Prediction Algorithm for Freight Train Wheels Based on Remaining Useful Life Prediction［J］. Mathematical Problems in Engineering， 2020， 2020：9256312.

［8］ LI Qi， ZHOU Jiayu， JIANG Zengqiang， et al. Train Wheel Degradation Modeling and Remaining Useful Life Prediction Based on Mixed Effect Model Considering Dependent Measurement Errors［J］. IEEE Access， 2019， 7：159058-159068.

［9］ 吕昊， 金雄程， 林录样. 基于Copula的车轮Gamma退化过程［J］. 东北大学学报（自然科学版）， 2021， 42（4）：544-549.

LYU Hao， JIN Xiongcheng， LIN Luyang. Wheel Gamma Degradation Process Based on Copula Function［J］. Journal of Northeastern University （Natural Science）， 2021， 42（4）：544-549.

［10］ DAI Xinliang， QU Sheng， SUI Hao， et al. Reliability Modelling of Wheel Wear Deterioration Using Conditional Bivariate Gamma Processes and Bayesian Hierarchical Models［J］. Reliability Engineering amp; System Safety， 2022， 226：108710.

［11］ YAN Bingxin， MA Xiaobing， HUANG Guifa， et al. Two-stage Physics-based Wiener Process Models for Online RUL Prediction in Field Vibration Data［J］. Mechanical Systems and Signal Processing， 2021， 152：107378.

［12］ 文永蓬， 尚慧琳， 董其炜， 等. 城市轨道车辆车轮轮缘磨耗分析［J］. 科技导报， 2013， 31（26）：40-43.

WEN Yongpeng， SHANG Huilin， DONG Qiwei， et al. Wear of Wheel Flange of Urban Rail Vehicle［J］. Science amp; Technology Review， 2013， 31（26）：40-43.

［13］ SI Xiaosheng， WANG Wenbin， CHEN Maoyin， et al. A Degradation Path-dependent Approach for Remaining Useful Life Estimation with an Exact and Closed-form Solution［J］. European Journal of Operational Research， 2013， 226（1）：53-66.

［14］ 牛一凡， 邵景峰. 基于非线性数据融合的设备多阶段寿命预测［J］. 信息与控制， 2019， 48（6）：729-737.

NIU Yifan， SHAO Jingfeng. Multistage Lifetime Estimation for Equipment Based on Nonlinear Data Fusion［J］. Information and Control， 2019， 48（6）：729-737.

［15］ 王洁宁， 张钰涵， 冀姗姗. 基于马尔科夫蒙特卡罗的管制员警觉概率预测［J］. 安全与环境学报， 2020， 20（4）：1412-1420.

WANG Jiening， ZHANG Yuhan， JI Shanshan. Probability Prediction of the Controller’s Status-in-situ Alertness Based on the Markov Chain Monte Carlo［J］. Journal of Safety and Environment， 2020， 20（4）：1412-1420.

［16］ 史朝阳， 王爱红， 高有山， 等. 基于MCMC的桥式起重机疲劳寿命可靠性灵敏度分析［J］. 中国安全科学学报， 2014， 24（3）：47-52.

SHI Zhaoyang， WANG Aihong， GAO Youshan， et al. Bridge Crane Fatigue Life Reliability Sensitivity Analysis Based on MCMC Method［J］. China Safety Science Journal， 2014， 24（3）：47-52.

［17］ 秦红志， 孙明娟， 王伟伟， 等. 二元性能相关多阶段退化系统可靠性建模与分析［J］. 运筹与管理， 2022， 31（3）：105-111.

QIN Hongzhi， SUN Mingjuan， WANG Weiwei， et al. Reliability Modeling and Analysis of Multi-stage Bivariate Degradation Process Systems［J］. Operations Research and Management Science， 2022， 31（3）：105-111.

［18］ 毛泽龙， 王治华， 吴琼， 等. 双指标阶段性退化建模及可靠性分析［J］. 系统工程与电子技术， 2021， 43（12）：3725-3731.

MAO Zelong， WANG Zhihua， WU Qiong， et al. Bivariate and Two-stage Degradation Modeling and Reliability Analysis［J］. Systems Engineering and Electronics， 2021， 43（12）：3725-3731.

［19］ 罗益， 卢勇， 黎澍， 等. 广州地铁1号线轮缘异常磨耗研究［J］. 城市轨道交通研究， 2023， 26（5）：251-254.

LUO Yi， LU Yong， LI Shu， et al. Research on Wheel Flange Abnormal Wear of Guangzhou Metro Line 1［J］. Urban Mass Transit， 2023， 26（5）：251-254.

［20］ 刘晓宇， 齐金平， 薛康， 等. 基于Wiener过程的城市轨道交通车辆轮对可靠性评估［J］. 铁路计算机应用， 2023， 32（4）：1-6.

LIU Xiaoyu， QI Jinping， XUE Kang， et al. Wheelset Reliability Evaluation of Urban Rail Transit Vehicles Based on Wiener Process［J］. Railway Computer Application， 2023， 32（4）：1-6.

（编辑 陈 勇）